3.1. Для расчета реостатной характеристики сначала определяются координаты точек, через которые должна проходить характеристика, и номинальный электромагнитный момент

По графику естественной характеристики находится скольжение при . Оно равно .

Скольжение на реостатной характеристике при заданных координатах:

Требуемое добавочное сопротивление:

Критическое скольжение, соответствующее реостатной характеристике:

Реостатная характеристика рассчитывается по формуле Клосса. Скорость определяется по следующей формуле: , где S – скольжение, которым задаются от 0 до 1,2. Далее по точкам строится характеристика.

ω, 1/c	-15,71	-7,85	0,00	7,85	15,71	23,56	31,42	39,27	47,12	54,98	62,83	70,69	78,54
S, о.е	1,20	1,10	1,00	0,90	0,80	0,70	0,60	0,50	0,40	0,30	0,20	0,10	0,00
M, Н•м	102,93	94,78	86,55	78,24	69,85	61,38	52,83	44,21	35,51	26,74	17,89	8,98	0,00

Реостатная характеристика изображена на рис. 5.

4.1. Расчет искусственной характеристики при заданных параметрах питающей сети

Параметры двигателя:

Механическая характеристика рассчитывается по формуле Клосса при подстановке в нее значений и .

ω, 1/c	-7,85	-3,93	0,00	3,93	7,85	11,78	15,71	19,63	23,56	27,49	31,42	35,34	39,27
S, о.е	1,20	1,10	1,00	0,90	0,80	0,70	0,60	0,50	0,40	0,30	0,20	0,10	0,00
M, Н•м	81,55	84,80	88,08	91,30	94,27	96,71	98,14	97,78	94,41	86,12	70,07	42,58	0,00

Скорость определяется по следующей формуле: , где S – скольжение, которым задаются от 0 до 1.2. Далее определяется момент М и по точкам строится искусственная характеристика. Она изображена на рис.5.

5.1. Для расчёта механической характеристики в режиме динамического торможения необходимо определить следующие параметры:

Номинальное сопротивление двигателя:

Добавочное сопротивление:

Ток возбуждения

Индуктивное сопротивление Х₀:

ЭДС фазы статора:

Номинальный ток намагничивания:

,

где .

Порядок расчета характеристики динамического торможения следующий:

1. Задаются током намагничивания в относительных единицах: в пределах от 0 до 1.

2. По универсальной кривой намагничивания (см. методические указания к заданию) по заданным значениям тока определяются соответствующие значения относительной ЭДС

3. Определяются значения и .

4. Определяется эквивалентный переменный ток статора:

5. Для каждого значения 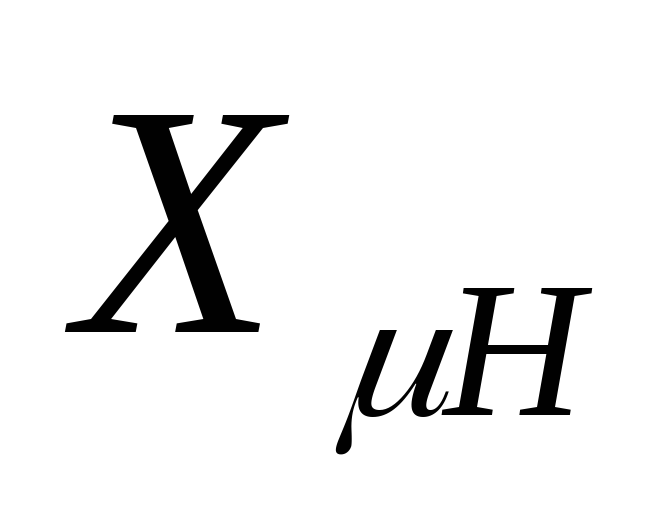определяется величина: .

6. Для каждого значения этой величины определяется ток ротора

7. Определяются соответствующие угловые скорости ротора:

8. Определяются значения электромагнитного момента:

Все расчеты сводятся в таблицу:

1
0,9
0,8

и т.д.

Рис 6. Примерный вид характеристики динамического торможения АД

9. По данным этой таблицы строится зависимость . Примерный вид этой зависимости изображен на рисунке 6.

6.1 Расчет пусковой диаграммы и соответствующих ей сопротивлений выполняется графоаналитическим методом (см. методические указания к заданию). Порядок расчета следующий:

1. Задаются пусковым моментом:

2. Задаются моментом переключения:

3. Полные активные сопротивления линии ротора на отдельных ступенях пуска будут равны:

4. Добавочные сопротивления пусковых ступеней:

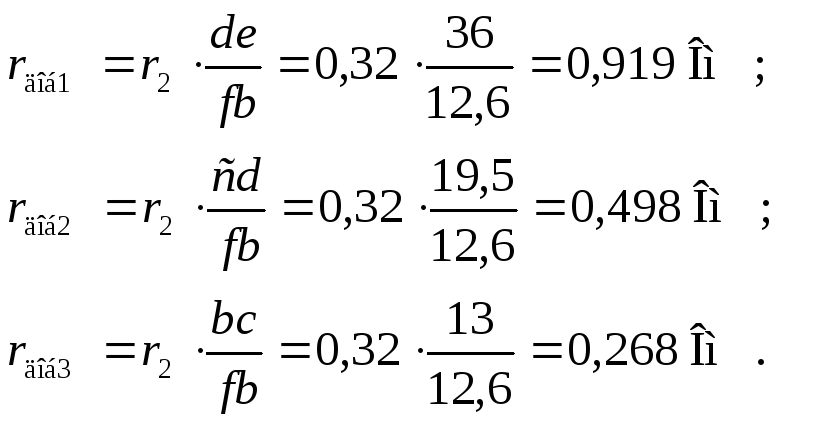
Лучевая диаграмма для расчёта пусковых сопротивлений изображена на рис.7.

Рис. 7. Лучевая диаграмма расчёта пусковых ступеней АДФР

Проверить возможность пуска двигателя при:

.

Вывод: Во всех трех случаях двигатель запустится т.к. Мс<M₁, и во всех случаях он выйдет на естественную характеристику, т. к. Мс<M₂

16