3.12. Явления при замыкании и размыкании тока. Энергия магнитного поля

Явления при замыкании и размыкании тока обусловлены индуктивностью цепи или самоиндукцией. Пусть, например, в цепь с аккумулятором включена катушка. Если каким-либо образом изменять ток в цепи, то собственный магнитный поток через катушку будет изменяться, и в цепи, помимо ЭДС аккумулятора, начнет действовать электродвижущая сила самоиндукции, которая по правилу Ленца будет препятствовать изменению питающего катушку тока. При этом удобно считать, что в дополнение к питающему току аккумулятора пойдет ток, вызванный ЭДС самоиндукции. Этот ток называется экстратоком или индукционным током. По правилу Ленца индукционный ток должен препятствовать причине (изменению начального тока в катушке), его вызвавшей. Следовательно, при увеличении тока в цепи индукционный ток потечет навстречу, а при уменьшении – в том же направлении, что и первичный ток.

Разберем явления, возникающие при замыкании и размыкании цепи. При замыкании цепи ток возрастает с нуля. Навстречу начинает течь индукционный ток (экстраток замыкания), который препятствует этому возрастанию. Поэтому ток в цепи достигает своего постоянного значения не сразу, а лишь через некоторое время, зависящее от величины индуктивности. Наоборот, при размыкании цепи ток исчезает не сразу, так как некоторое время течет экстраток размыкания, направленный так же, как и первичный ток. Отметим, что при резком размыкании цепи при определенных условиях величины ЭДС самоиндукции и экстратока размыкания могут быть велики, и превышать ЭДС источника величину тока, текущего до размыкания цепи. Поэтому на предприятиях для того, чтобы не повредить электрооборудованиеие, напряжение отключают не сразу, а понижают до нуля постепенно.

Теперь рассмотрим количественную оценку этого явления. Цепь, состоящая из источника постоянного тока с ЭДС , катушки с индуктивностью и сопротивления, представлена на рис. 3.20. Полное сопротивление цепи (с учетом сопротивления обмотки катушки, внутреннего сопротивления источника) обозначим. При замыкании ключаК в первый момент помимо ЭДС  в цепи действует также ЭДС самоиндукции _s. По закону Ома сила тока .

Учитывая формулу (3.26, а), получаем дифференциальное уравнение относительно функции :

.

Общее решение этого уравнения имеет вид

.

Величина константы С определяется из начального условия, показываю­щего, что в момент замыкания (при ) ток равен нулю. В итоге получим, что, и сила тока:

, (3.27)

где  постоянная, имеющая размерность времени и называемая временем установления тока. Из формулы (3.27) видно, что полный ток состоит из двух слагаемых. Слагаемое пред­став­ляет собой экстраток замыкания. По прошествии достаточно большого времени экстраток замыкания становится очень малым, т.е. приостается лишь второе слагаемое, представляющее собой величину постоянного установившегося тока. Итак, ток в цепи устанавливается постепенно. Время установления определяется величиной, зависящей от индуктивности и сопротивления цепи. Величинапо сути представляет собой время, за которое экстраток замыкания уменьшается враз. В качестве упражнения предоставляем читателям самостоятельно построить графики зависимостейпо формулам (3.27), (3.29).

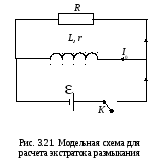
Исследуем процесс размыкания цепи, представленной на рис. 3.21. Общий ток в цепи распределяется между катушкой с сопротивлением и индуктивностью ии сопро­тив­ле­ни­ем. Сопротивление источника тока будем считать очень малым. При замкнутом ключе ток, текущий через катушку. При размыкании клю­ча ток в замкнутом контуре катушки и сопротивления падает до нуля не сразу, поскольку в контуре начинает действовать поддержи­ваю­щая ток ЭДС самоин­дук­ции. Согласно закону Ома ве­ли­чи­на тока в контуре. Применяя формулу (3.26,а), получим:

. (3.28)

Отсюда следует дифференциальное уравнение

,

которое решается с учетом начального условия (при сила тока). В момент перед размыканием ключа через катушку идет ток, а через сопротивлениеидет ток. Но поскольку резисторобладает пренебрежимо малой индуктивностью, можно считать, что начальный ток в замкнутом контуре после размыкания ключа равен току через катушку. С учетом этого решение дифференциального уравнения имеет вид

, (3.29)

где . Решение (3.29) представляет собой экстраток размыкания. При. Величинапредставляет собой время, за которое сила тока в контуре убывает в е раз.

Дифференцируя выражение (3.28), найдем значение ЭДС самоиндукции:

.

Видно, что при условии в начальный момент времени после размыкания цепи величина ЭДС самоиндукции во много раз может превзойти значение. Это можно показать на опыте, заменив сопротивлениелампочкой и соответствующим образом подобрать параметры цепи. Например, еслиВ, можно взять лампочку, рассчитанную на 10 В. При замкнутом ключе лампочка будет гореть тускло. При размыкании ключа она на мгновение ярко вспыхивает. А если ЭДС индукции во много раз превысит значение ЭДС батареи, лампочка может даже перегореть.

Рассмотрим теперь явление размыкания цепи (рис. 3.21) с точки зрения закона сохранения энергии. Будем предполагать, что вместо резистора в цепь включена лампочка. Откуда же берется энергия, затраченная на вспышку лампочки? Источник тока уже отключен и не отдает энергию в контур. Следовательно, запасом энергии обладает катушка с током. Эту энергию она получила от аккумулятора, когда ключ был замкнут. В процессе самоиндукции при исчезновении тока в катушке её энергия и переходит в энергию вспышки.

Что собой представляет энергия катушки с током? В начальный момент времени по катушке идет ток , который создает магнитное поле. Исчезновение тока в катушке означает исчезновение магнитного поля. Значит, по сути, энергия катушки с током – это энергия её магнитного поля. Таким образом, при размыкании цепи в процессе самоиндукции именно энергия магнитного поля катушки переходит в энергию вспышки.Магнитное поле – форма материи, обладающая энергией.

Рассчитаем энергию магнитного поля катушки с током. Преобразуем формулу (3.28): . Помножим обе части последнего уравнения на:

. (3.30)

По закону Джоуля-Ленца левая часть (3.30) представляет собой количество теплоты , выделившееся в резистореза время. Значит уравнение (3.30) можно переписать в виде:

. (3.30,а)

Проинтегрируем обе части уравнения (3.30,а), учитывая, что начальный ток равен , а конечный ток равен нулю:

.

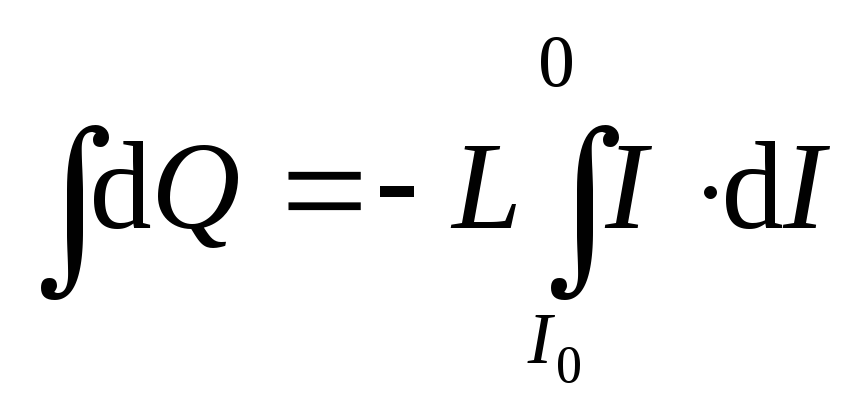
Поскольку на сопротивлении тепло выделяется за счет энергии магнитного поля катушки, правая часть полученного уравнения должна представлять собой энергию катушки. Таким образом, энергия магнитного поля катушки с током:

(3.31)

Формула (3.31) остается справедливой и для энергии магнитного поля произвольного контура с индуктивностью и током.

В дальнейшем будет выведено выражение для плотности энергии электромагнитного поля катушки с током (пример 3.17, стр.136).