2.4. Источники тока. Закон Ома для полной цепи

Для того чтобы поддерживать разность потенциалов на концах проводника и, следовательно, существование постоянного электрического тока в проводнике и постоянное тепловыделение, необходимы источники электрической энергии (электрического тока). В источниках такого рода происходит разделение зарядов разных знаков и на выходных клеммах появляется разность потенциалов.

Подключим какую-нибудь нагрузку (сопротивление) к источнику электрической энергии. Получим замкнутую цепь. Каким образом движутся заряды вне и внутри источника тока? Прежде всего, еще раз напомним, что мы рассматриваем только стационарные токи, т.е. заряды нигде не накапливаются, а просто циркулируют по замкнутой цепи. Вне источника (во внешней цепи) ток идет от «плюса» к «минусу» (клемма «плюс» – клемма с большим потенциалом, клемма «минус» – клемма с меньшим потенциалом). Таким образом, во внешней цепи заряды движутся в направлении, в котором на них действует электрическое поле внутри проводника: положительные по полю, отрицательные против поля. Внутри источника электрической энергии (во внутренней цепи) ток идет от «минуса» к «плюсу», т.е. заряды движутся в направлении, противоположном тому, в котором на них действует электрическое поле. Значит, внутри источника перемещение зарядов вызывается не электрическим полем, а какими-то иными причинами. Эти причины (химические, механические, световые, магнитные и т. д.) зависят от природы источника тока.

Силы, действующие внутри источника электрической энергии, заставляющие заряды двигаться против действия электрического поля, называются сторонними силами. При этом часто при решении каких-то задач природа этих сил значения не имеет и не конкретизируется. Сторонние силы при упорядоченном движении зарядов совершают работу, за счет которой, например, нагреваются сопротивления. Очевидно, что полный запас энергии источника тока равен работе, которую могут совершить сторонние силы.

К идее о необходимости действия в замкнутой цепи сторонних сил полезно прийти и иным образом. Представим себе, что на свободные заряды в замкнутой цепи действовали бы одни электрические силы. Известно, что цепь при прохождении по ней тока нагревается. Выделившееся тепло тогда можно было бы рассматривать только как результат работы электрических сил (электрического поля). Но работа электрического поля по перемещению зарядов по замкнутой траектории (в данном случае замкнутой цепи) равна нулю (этот факт подробно обсуждался в п.1.12). А значит, не могла бы нагреваться и цепь, что явно противоречит опыту. Следовательно, где-то в замкнутой цепи обязательно должны действовать силы не электростатического происхождения, работа которых отлична от нуля, т.е. сторонние силы. Место действия сторонних сил в замкнутой цепи и можно назвать источником электрической энергии или источником тока.

Важнейшей характеристикой источника тока является электродвижущая сила (ЭДС). Можно дать два эквивалентных определения ЭДС.

1) ЭДС – разность потенциалов на выходных клеммах источника тока при разомкнутой внешней цепи (или когда ток через источник не идет). Далее мы покажем, что в случае разрядки или зарядки источника тока разность потенциалов на его выходных клеммах соответственно меньше ЭДС и больше ЭДС.

2) ЭДС – работа сторонних сил (источника) по разделению единичного заряда (или просто при прохождении через источник единичного заряда):

. (2.12)

Из (2.12) следует, что, зная ЭДС источника, силу тока и время его протекания, можно определить работу, совершенную сторонними силами:

. (2.13)

Обсудим вторую характеристику источника – внутреннее сопротивление. Представим себе, что мы замкнули клеммы источника проводником с исчезающе малым сопротивлением , другими словами, сделали короткое замыкание источника. Тогда, если бы источник был идеальным, т.е. на его выходных клеммах разность потенциалов была бы всегда равна ЭДС, то по закону Ома мы получили бы, т.е. источник давал бы бесконечный ток и в единицу времени совершал бы бесконечно большую работу (см. (2.13)), что невозможно. Таким образом, при работе любого источника обязательно должны существовать какие-либо внутренние механизмы ограничения максимального тока. Эти механизмы могут быть различными в зависимости от природы источника тока. Однако все они могут быть смоделированы, если ввести вторую характеристику источника – внутреннее сопротивление. В этом случае при коротком замыкании за счет конечного внутреннего сопротивления источника мы получим конечный ток в цепи, называемый током короткого замыкания:. Это максимальный ток, который может давать источник. Итак, внутреннее сопротивление источника– это характеристика, определяющая ток короткого замыкания или максимальные ток и мощность, которые может давать источник.

Можно сделать вывод, что какова бы ни была сложная природа источника тока, его можно охарактеризовать всего двумя параметрами – электродвижущей силой (ЭДС) и внутренним сопротивлением. Любой источник тока можно представлять себе как «черный ящик», состоящий из идеального источника ЭДС , разность потенциалов на клеммах которого всегда равна, и после­до­вательно соединенного с ним сопротивленияr, ко­то­рое называется внутрен­ним сопротив­ле­нием источника тока. Такая модель источника тока показана на рис. 2.9.

На этом же рис. 2.9 к клеммам источника подключено некоторое, отличное от нуля сопротивление R. Поскольку внутреннее и внешнее сопротивления соединены последовательно, полное сопротивление цепи будет , и по цепи потечет ток:

. (2.14)

Последнее равенство называется законом Ома для полной цепи.

Уравнение (2.14) легко преобразуется к виду: . Правая часть этого равенства (а значит и левая) есть напряжение на внешнем сопротивленииR. Это напряжение суть напряжение на выходных клеммах источника тока, так как сопротивление R непосредственно к этим клеммам подключено. Таким образом, при разрядке источника током I напряжение на его клеммах:

. (2.15)

Это напряжение тем ближе к ЭДС, чем меньше внутреннее сопротивление и ток разрядки. При в соответствии с данным выше первым определением ЭДС из (2.15) получим.

Пример 2.7. В схеме на рис. 2.9 В,Ом,Ом.

1. Определить силу тока в цепи. По закону Ома для полной цепи (2.14) получим: А.

2. Определить напряжение на клеммах источника тока. Напряжение на клеммах источника суть напряжение на нагрузке R: 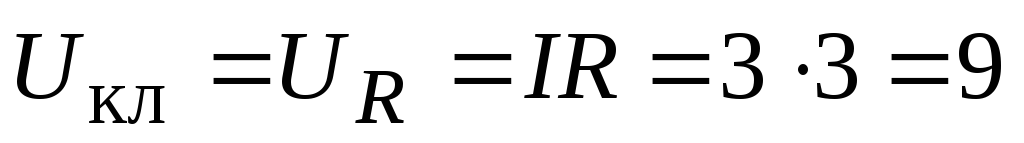В. Естественно то же самое получается и по формуле (2.15).

3. Определить мощность, выделяющуюся во внешней цепи. Мощность, выделяющаяся во внешней цепи, есть мощность, выделяющаяся на нагрузке R, поэтому: 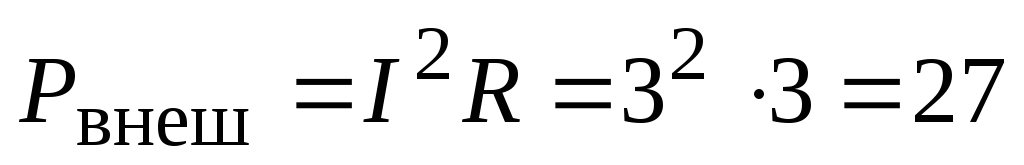Вт.

4. Определить мощность, выделяющуюся во внутренней цепи. Конечно, при работе источника тока нагревается не только внешняя нагрузка, но и сам источник, поскольку он обладает внутренним сопротивлением. Мощность, выделяющаяся во внутренней цепи, есть мощность, выделяющаяся на сопротивлении r: Вт.

5. Определить мощность источника тока (мощность, развиваемую сторонними силами). Работа источника тока расходуется на нагревание как внешней нагрузки, так и самого источника тока, поэтому: Вт. Можно рассуждать и по-другому, опираясь на уравнение (2.13):Вт.

6. Определить КПД схемы. Полезной следует считать часть мощности источника, которая выделяется на внешнем сопротивлении, поэтому:

(или 75%).

7. Определить максимальный ток, который может давать заданный источник. Ток будет максимален при коротком замыкании источника (т.е. при ):

(А).

Пример 2.8. Каким должно быть сопротивление при заданных параметрах источника тока и r для того, чтобы во внешней цепи выделялась максимальная мощность? Чему равна эта максимальная мощность?

Решение. Пользуясь законом Ома для полной цепи (2.14) для мощности, выделяемой во внешней цепи, можно записать:

(2.16)

Р_внеш

R₁ R=r R₂ R

Рис. 2.10. Зависимость мощности, выделяемой во внешней цепи от сопротивления

График зависимости функции показан на рис. 2.10. Ясно, что эта функция должна иметь точку максимума (т.е. значение , при котором мощность во внешней цепи максимальна), поскольку из (2.16) следует, что ипри. Найдем точку максимума функции. Для этого продифференцируемпо сопро­тив­лениюи приравняем произ­вод­ную к нулю:

,

откуда получаем: . Таким образом, мощность, выделяемая во внешней цепи максимальна, когда внешнее сопротивление равно внутреннему сопротивлению источника (рис. 37).

По формуле (2.16) рассчитаем максимальное значение мощности, выделяемой во внешней цепи:

.

Отметим, что КПД схемы при этом равен всего на всего 50%, т.е. половина мощности выделяется во внешней цепи и половина – во внутренней:

.

Анализируя график на рис. 2.10, можно сделать вывод, что какое-то требуемое значение мощности, выделяемой во внешней цепи, можно получить двумя способами: подключая к источнику тока некоторые сопротивления и, причем, а. Какой вариант следует выбрать? Конечно, предпочтение следует отдать второму варианту (т.е. включить большее сопротивление), поскольку КПД схемы в этом случае будет больше (см. вопрос 6 примера 2.5). При подключении же сопротивленияКПД будет меньше 50%. Во внешней цепи мы тоже получим требуемую мощность, но при этом еще большая мощность будет бесполезно выделяться во внутренней цепи, т.е. расходоваться на нагрев самого источника. В результате источник быстрее израсходует свой ресурс.