
Гладков_Кулютникова Информатика
.pdf13 Гладков В.П., Кулютникова Е.А. Пособие по информатике для самообразования.
Перевести числа 73638, 12345678 в шестнадцатеричную систему счисления двумя способами.
_________________________________________________________________________
Проверьте себя: F7316, 5397716.
Выполнение арифметических операций в позиционных системах счисления
Арифметические операции выполняются во всех позиционных системах счисления одинаково по следующим правилам.
Сложение выполняется поразрядно для чисел, записанных друг под другом и выровненных вправо по разряду единиц. Если при сложении цифр в текущем разряде с учетом единицы переноса из младшего разряда сумма получилась больше основания системы счисления, то из нее вычитается основание системы счисления, результат записывается в текущем разряде и запоминается единица переноса в старший разряд. Если сумма получилась меньше основания системы счисления, то она записывается в данный разряд.
Пример.
|
|
+ |
11111 |
|
+ 7158 |
|
+ |
A13 |
||||
|
|
2 |
|
3738 |
|
16 |
|
|||||
|
|
|
10012 |
|
|
|
1CF16 |
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1010002 |
|
1310 |
8 |
|
|
BE 216 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Упражнение. Найдите сумму |
|
|
|
|
||||||||
1. |
101012 + 1012; |
110102 + 10112; |
101012 + 10112 |
|||||||||
2. |
5248 + 578; |
57318 + 13768; |
321,78 + 765,48 |
|||||||||
3. F0B16 + 1DA16; |
2EA16 + FCE16; |
A2F816 + FDA16. |
||||||||||
________________________________________________________________________
Проверьте себя: 110102, 1001012, 1000002; 6038, 73278, 1307,38; 10E516, 12B816, B2D216.
Вычитание выполняется поразрядно для чисел, записанных друг под другом и выровненных по разряду единиц. Если разряд уменьшаемого больше разряда вычитаемого, то их разность записывается в текущий разряд. В противном случае занимается единица из старшего разряда, которая равна p единицам младшего разряда (p - основание системы счисления), и производится вычитание.
Пример.
_ 1000112 |
|
_ 4368 |
|
|
_ DFA16 |
||||
|
|
1102 |
|
1378 |
|
|
1AE16 |
||
|
|
|
|
|
|
|
|
|
|
|
|
10112 |
|
2778 |
|
|
C4C16 |
||
Упражнение. Найдите разность: |
|
|
|
||||||
1. |
1010002 - 112; |
1000012 - 10012; |
1000102 - 1012 |
||||||
2. |
1378 - 72,18; |
7058 - 76,38; |
71358 - 7568 |
||||||
3. F0516 - AD,316; |
EA3516 - FC816; |
F1C516 - DEB16. |
|||||||
________________________________________________________________________
Проверьте себя: 1001012, 110002, 1111012; 44,78, 606,58, 61578; E57,D16, DA6D16, E3DA16.
14 Гладков В.П., Кулютникова Е.А. Пособие по информатике для самообразования.
Умножение осуществляется на основе таблицы умножения поразрядно справа налево. При перемножении текущих разрядов результат определяется по таблице умножения с учетом переноса из младшего разряда. Единицы переносятся в результат. Остальные разряды составляют перенос в следующий разряд. Промежуточные поразрядные произведения записываются друг под другом со сдвигом влево на один разряд, складываются, и получается результирующее произведение.
Пример. Найти произведение.
х 101012 |
х10012 |
__10112 |
____112 |
10101 |
+1001 |
+10101 |
1001 |
10101___ |
110112 |
111001112 |
|
Пример. Найти Х из условия: х268 - 1х38 = 34х10. Пример. Найдите x из условия x268-1x38=34x10.
Представим все числа в форме многочлена:
2 2 2
x· 8 + 2· 8 + 6 - (1· 8 + x· 8 + 3) = 3· 10 + 4· 10 + x.
Приведем подобные члены и получим уравнение: 55х - 385 = 0. Решение этого уравнения х =7.
Поскольку 7 может быть цифрой восьмеричной или десятичной систем счисления, то ее можно рассматривать в качестве ответа.
Правильность найденного решения нужно проверить непосредственной его подстановкой в заданное условие:
7268 = 7· 82 + 2· 81 + 6· 80 = 47010 1738 = 1· 82 + 7· 81 + 3· 80 = 12310 47010 - 12310 = 34710
34710 = 34710
Ответ: х = 7.
Упражнения.
1. Определите основание системы счисления, исходя из равенства:
а) 202х - 121х = 224х - (х10 + 1)2. б) 121х + B16 = (х10 + 102)2.
в) 135x+250x=1x110.
г) 3232x·45x-1353x-2=5133x. д) 12.2x+6.62x=13.2510.
е) (500x+1-21x+23x):112x=30x. ж) 833x:22x=51.62x+2.
з) 132x·2x6=2040x+2.
и) xx2x=130.5x·22x+220.5x. к) 112·21x+1020.5x=126x-1.
л) 20x(x10+102·57x)-510x=2430x.
2.Опишите способ перевода числа, записанного в троичной системе счисления, в девятеричную, минуя десятичную систему счисления.
3.Даны числа, записанные в различных системах счисления. Найдите для каждого их них предыдущее и последующее:
21223, 7778, 10012, 3445, 11012, 2203.
15Гладков В.П., Кулютникова Е.А. Пособие по информатике для самообразования.
4.Переведите в двоичную, шестеричную, восьмеричную и шестнадцатеричную системы счисления 87,1710.
________________________________________________________________________
Проверьте себя:
1. а) - 4, б) – 6, в) – 6, г) – 3, д) – 4, е) – 6, ж) - -5, з) – 5, и) – 8, к) – 8, л) –8.
2. Поскольку девять – это квадрат тройки, то нужно разбить число от разряда единиц влево по две цифры и каждую пару троичных цифр заменить цифрой девятеричной системы счисления в соответствии с таблицей:
Троичная с/с |
Девятеричная с/с |
00 |
0 |
01 |
1 |
02 |
2 |
10 |
3 |
11 |
4 |
12 |
5 |
20 |
6 |
21 |
7 |
22 |
8 |
3. Сверьте результаты: |
|
|
|
|
|
|
|
|
предыдущее |
21213 |
7768 |
10002 |
3435 |
11002 |
2123 |
|
исходное |
21223 |
7778 |
10012 |
3445 |
11012 |
2203 |
|
следующее |
22003 |
10008 |
10102 |
4005 |
11102 |
2213 |
4. |
1010111.001010111000010100011112 |
|
|
|
|||
|
223.1(004153)6 |
|
|
|
|
|
|
127.127024368 57.(2B851E)16.
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
В основе математической логики лежат высказывания, которыми может быть любое утверждение (или повествовательное предложение), о котором можно сказать истинно (true) оно или ложно (false). Истину и ложь будем обозначать соответственно 1 и 0.
Для составления сложных высказываний используют простые высказывания, соединяя их знаками логических операций: “ не” ( логическое отрицание или инверсия), “ и” (логическое умножение или конъюнкция), “ или” ( логическое сложение или дизъюнкция).
Правила выполнения логических операций задаются с помощью специальных таблиц, которые называются таблицами истинности.
Таблица истинности отрицания:
А |
|
¬А |
Высказывание: “ Мы любим оперу”, отрицание этого высказывания: |
|
1 |
|
0 |
“ Мы не любим оперу”. |
|
0 |
|
1 |
Высказывание: x ³ y, отрицание: x < y. |
|
|
Таблица истинности конъюнкции: |
|||
A |
|
B |
A Ù B |
Конъюнкция дает истину, когда оба операнда истинные, в |
0 |
|
0 |
0 |
остальных случаях - ложь. |
0 |
|
1 |
0 |
Высказывание: “ А и В сидели на трубе” истинно, когда и А |
1 |
|
0 |
0 |
и В одновременно сидят на трубе. Если одного из них или |
1 |
|
1 |
1 |
обоих сразу нет, то все высказывание становится ложным. |

16 Гладков В.П., Кулютникова Е.А. Пособие по информатике для самообразования.
Таблица истинности дизъюнкции:
A |
B |
A B |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
Дизъюнкция дает ложь только в том случае, когда оба операнда ложны, в остальных случаях - истина. Высказывание: ” Мы пойдем купаться сегодня или завтра” ложно в том случае, если мы пошли купаться послезавтра. Но истинно, если пошли купаться сегодня, завтра, а также и сегодня и завтра.
Введем еще две логические операции: импликация ( ) и эквивалентность ( ).
A |
B |
A B |
Из истины не может следовать ложь. |
0 |
0 |
1 |
Из лжи может следовать все, что угодно. |
0 |
1 |
1 |
Примеры. Если 2 х 2 = 4, то Волга впадает в Каспийское море. |
1 |
0 |
0 |
Когда рак на горе свистнет, будет получено молоко от козла. |
1 |
1 |
1 |
Бузина в огороде влечет за собой дядьку в Киеве. |
|
|
|
|
A |
B |
A B |
Если высказывания А и В одинаковы, то операция дает ис- |
0 |
0 |
1 |
тинный результат. |
0 |
1 |
0 |
Примеры. Число простое, если оно делится на 1 и на само себя. |
1 |
0 |
0 |
Я поеду в Москву тогда и только тогда, когда ты поедешь в Киев. |
1 |
1 |
1 |
sin 30° равен 0.5 |
Логические законы
Два высказывания являются равносильными (≡), если на одинаковых наборах данных они принимают одинаковые значения, т.е. для доказательства логических законов необходимо установить какие значения принимают обе части высказывания на всевозможных значениях переменных, входящих в высказывание. Такой подход возможен благодаря небольшому количеству исходных данных.
1. коммутативные (перестановочные) законы
A B ≡ B A A B ≡ B A .
Пример. “ А и В сидели на трубе” равносильно “ В и А сидели на трубе”.
2. ассоциативные (сочетательные) законы
( A B) C ≡ A ( B C) ( A B) C ≡ A ( B C)
Пример. “ Мы с подружкой Юлей дружим с Сашей” равносильно “ Я дружу с Юлей и Сашей”.
3. дистрибутивные (распределительные) законы
A ( B C) ≡ ( A B) ( A C) A ( B C) ≡ ( A B) ( A C)
Пример. “ Я дружу с Алексеем или Васей и Петей” эквивалентно “ Я дружу с Алексеем или Васей и дружу с Алексеем или Петей”.
4. закон двойного отрицания
A ≡ A
Пример. “ Неверно, что умный в гору пойдет” эквивалентно “ Умный в гору не пойдет”. “ Неверно, что курица не птица” эквивалентно “ Курица - птица”.

17 Гладков В.П., Кулютникова Е.А. Пособие по информатике для самообразования.
5. законы де Моргана
A B ≡ A B ; A B ≡ A B
Пример. Отрицание фразы “ Наша служба опасна и трудна” может иметь две формы: а). неверно, что наша служба и опасна и трудна (левая часть закона).
б). наша служба или не опасна или не трудна (правая часть закона).
Для фразы “ Была прочна палатка или был не страшен путь” есть два варианта отрицания:
а) неверно, что была прочна палатка или был не страшен путь (левая часть закона); б) была не прочна палатка и был страшен путь (правая часть закона).
6. |
законы идемпотентности |
|
|
A A ≡ A |
A A ≡ A |
7. |
закон исключающего третьего |
|
A A ≡ 1
Пример. У меня есть компьютер или у меня нет компьютера, третьего не дано.
8. закон непротиворечивости
A A ≡ 0
Одновременно не могут быть истинными высказывание и его отрицание.
Пример. Я не Рафаэль и я - Рафаэль, т.е. одновременно нельзя быть и не быть Рафаэлем.
9. законы, определяющие действия с логическими константами 0 и 1.
|
1 A ≡ 1 |
1 A ≡ A |
0 A ≡ A |
0 A ≡ 0 |
||||
10. |
законы поглощения |
|
|
|
|
|||
|
A ( A B) ≡ A |
A ( A B) ≡ A |
||||||
11. |
закон склеивания |
|
|
|
(A B) (A |
|
)≡ A |
|
|
|
|
|
|
||||
|
( A B) ( A |
|
) ≡ A |
B |
||||
|
B |
|||||||
Пример. Фрекен Бок рассуждала следующим образом: “ У меня жужжит в правом ухе и в левом или у меня жужжит в правом ухе, но не жужжит в левом”. Используя данный закон, можно было бы сказать, что у фрекен Бок жужжало только в правом ухе.
Рассмотрим доказательство закона дистрибутивности конъюнкции относительно дизъюнкции: A (B C) ≡ (A B) (A C).
A B C B C A (B C) A B A C (A B) (A C)
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |

18 Гладков В.П., Кулютникова Е.А. Пособие по информатике для самообразования.
Столбики 5 и 8 полностью совпали, следовательно, закон доказали.
Упражнения.
1. Докажите тождества: 1). X X (Y Y) ≡1
2). A Ù B Ù C Ú A Ú B Ú C º 1
2.Докажите ассоциативные законы и законы де Моргана.
3.Сформулируйте на русском языке отрицание фраз:
·летом мы пойдем в лес и не встретим волка;
·или кошка поймает мышку, или мышка обманет кошку;
·он ел одну лишь травку и с мухами дружил;
·это мы не проходили и это нам не задавали;
·это мы не проходили или это нам не задавали;
·скатертью дальний путь стелется и упирается прямо в небосклон;
·никогда не разрешайте ставить градусник себе, и таблеток не глотайте, и не ешьте порошков.
4. Определите значение истинности следующих высказываний:
*если 2 х 2 = 5, то лучший друг Чебурашки - крокодил Гена;
*если 2 х 2 = 5, то лучший друг Чебурашки - старуха Шапокляк;
*Шерлок Холмс и доктор Ватсон - знаменитые сыщики тогда и только тогда, когда лиса Алиса и кот Базилио - знаменитые плутишки;
*4 - простое число или Белоснежка знакома с 7 гномами;
*Колобок ушел от волка и от лисы;
*Мойдодыр - герой сказки Пушкина, а Балда - герой сказки Чуковского;
*Мойдодыр - герой сказки Чуковского или Балда - герой сказки Чуковского;
*Мойдодыр - герой сказки Чуковского, а Балда - герой сказки Пушкина;
*Карл у Клары украл кораллы, а Клара у Карла украла кларнет или ехал Грека через реку, но не увидел в реке рака;
5. Нарисуйте на плоскости X, Y область, в которой и только в которой выполняется
следующее условие: (x ³ y) Ù (x + y ³ 0) Ù (y £ 1).
АЛГОРИТМ И ЕГО СВОЙСТВА
Понятие алгоритма относится к числу основных, самых общих понятий информатики, также как понятия точки, линии, плоскости в геометрии. Поэтому определяется это понятие с помощью описания.
Алгоритм - это последовательность действий, ведущих от исходных данных к нужному результату, удовлетворяющая трем основным свойствам:
1)определенности (детерминированности);
2)массовости;
3)конечности.
Прежде всего, определение подчеркивает то, что алгоритм носит дискретный характер (последовательность действий). Свойство детерминированности состоит в понятности каждого действия алгоритма его исполнителю. Если это не так, то при исполнении алгоритма возникает АВОСТ (аварийная остановка), потому что исполнитель не может или не умеет исполнять непонятное действие.
Свойство массовости состоит в способности алгоритма решать не одну задачу, а целый класс подобных, отличающихся конкретными значениями исходных данных задач.
19 Гладков В.П., Кулютникова Е.А. Пособие по информатике для самообразования.
Свойство конечности гарантирует получение результата за конечное время. При этом не нужно прилагать интеллектуальных усилий, достаточно только точно и аккуратно выполнять все действия, указанные в алгоритме.
Примерами алгоритма являются правила выполнения арифметических операций в позиционной системе счисления, описание передвижения человека в городе от одной точки до другой, рецепт приготовления кулинарного блюда или лекарства, деления отрезка прямой или угла пополам.
Алгоритмами не являются процесс рисования картины художником или решения задачи, процесс воспитания человека. Для решения одной и той же задачи можно предложить несколько алгоритмов. Например, переместиться из одной точки города в другую можно несколькими способами.
Существуют задачи, для которых нельзя построить алгоритм. Такие задачи называются алгоритмически неразрешимыми. Примерами таких задач являются задача об удвоении куба (построить с помощью циркуля и линейки куб, объем которого в два раза больше объема данного куба), задача о разбиении угла на три равные части с помощью циркуля и линейки (трисекция угла) и т.п.
Алгоритмы используются при обработке данных на компьютере, при управлении космическими кораблями, для резервирования билетов на транспорт, для управления сложными объектами и т.п.
Пример. Алгоритм покраски забора:
1.Взять краску и кисть.
2.Подойти к первой доске забора.
3.Пока забор не закончился, повторять:
3.1.Покрасить доску.
3.2.Подойти к следующей доске.
4.Убрать на место краску и кисть.
5.Вымыть руки.
Свойство массовости этого алгоритма состоит в том, что, руководствуясь им, можно покрасить любой забор любой краской. Свойство конечности гарантирует, что, используя этот алгоритм, можно покрасить забор за конечное время.
Упражнение.
1.Приведите пример алгоритма. Покажите его свойства.
2.Приведите пример не алгоритма. Укажите, какие свойства в нем нарушены.
Существуют три формы представления алгоритма:
*на естественном языке;
*в виде блок-схемы;
*на алгоритмическом языке.
Пример. Описать алгоритм решения задачи: полторы кошки за полтора часа съедают полторы мышки. Сколько мышек съедят M кошек за N часов?
1.Алгоритм на естественном языке будет выглядеть следующим образом:
1.Ввести количество кошек М и часов N.
2.Одна кошка за полтора часа съест одну мышку, а за один час - 1/1,5 мышек.
3.Общее количество съеденных мышек определится по формуле: 1/1,5 * M * N.
2.Блок-схема алгоритма:
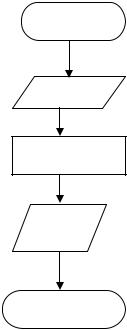
20 Гладков В.П., Кулютникова Е.А. Пособие по информатике для самообразования.
НАЧАЛО
N, M
k=1/1.5*M*N
k
КОНЕЦ
3. Программа на Паскале program task1;
var M, N: integer;
K : real; begin
write(‘Введите количество мышек и количество часов’); readln (M, N);
K := 1/1.5 * M * N;
writeln (‘будет съедено’, K:10:3, ‘мышек’);
end.
В зависимости от последовательности выполнения шагов алгоритма выделяют три типа вычислительных процессов:
*линейные;
*ветвящиеся;
*циклические.
Линейные алгоритмы представляют собой простые последовательности операторов, приводящие к получению результата без изменения порядка их следования. Эти алгоритмы характерны для расчетов по цепочке формул, когда результаты предыдущих вычислений используются последующими до получения искомых значений. Линейные алгоритмы также являются составным элементом циклического или ветвящегося алгоритма, их повторяющимся участком или ветвью. Задача о кошках-мышках представляет собой линейный алгоритм.
Ветвящийся (разветвляющийся) алгоритм - алгоритм, в котором в зависимости от результатов проверки некоторого условия выполняется одна из двух заранее предусмотренных ветвей. При движении по любой ветви может встретиться еще один логический блок, который образует еще две ветви и т.д. Но независимо от структуры, сложный или простой алгоритм, всегда имеется только один блок “ конец”.
Пример 2. Если кошка прячет нос, то будет холодно, иначе - тепло.
Пример 3. Если температура ниже -25°, то физкультура будет в зале, иначе - на улице.
21 Гладков В.П., Кулютникова Е.А. Пособие по информатике для самообразования.
program task2; var t: integer; begin
write (‘Какая сегодня температура?’); readln (t);
if t <= - 25 then writeln (‘физкультура будет в зале’) else writeln(‘физкультура будет на улице’);
end.
Циклический алгоритм - алгоритм, в котором выполнение некоторых операторов (групп операторов) повторяется многократно. Группа действий, повторяющихся в цикле, называется телом цикла. Однократное выполнение тела цикла - шаг. Для того чтобы цикл не стал бесконечным (не зациклился), им надо управлять. Для этого используется специальная величина - параметр (переменная) цикла - это такая величина, которая изменяется от шага к шагу и по значению которой определяется продолжать или закончить выполнение тела цикла.
Существуют циклы, для которых заранее известно количество раз выполнения тела.
Такие циклические алгоритмы называют арифметическими или циклами с параметром
(счетчиком).
Пример 4. Алгоритм покраски забора. От первой доски до десятой повторять:
1.покрасить доску;
2.сделать шаг вправо, перейти к следующей доске.
Это арифметический цикл с положительным шагом (номера досок увеличиваются). Пример 5. Алгоритм покраски забора.
От десятой доски до первой повторять:
1.покрасить доску;
2.сделать шаг влево, перейти к следующей доске.
Это арифметический цикл с отрицательным шагом (номера досок уменьшаются). Как правило, доски в заборах никто не считает, и логично было бы представить
рассмотренный выше алгоритм в следующем виде: Пока забор не закончился, повторять шаги 1 и 2. Или
Повторять шаги 1 и 2 до тех пор, пока забор не закончился.
Такие циклы называют итерационные, в первом случае - с предусловием, во втором - с постусловием. Для таких циклов заранее не известно количество раз выполнения тела, но существует только одна причина окончания.
Задача покраски забора может быть сформулирована еще и таким образом: красить забор до тех пор, пока не встретится покрашенная доска (для случая, если забор частично покрашен), т.е. повторяются действия:
если очередная доска не покрашена и это не конец забора, то красить доску и делать шаг вправо.
Такой цикл называют цикл поисковым. Он может быть завершен по двум причинам: 1) найдена покрашенная доска; 2) забор кончился, покрашенная доска не была найдена.
Упражнения.
1.Какие формы представления алгоритмов существуют? Приведите пример алгоритма во всех его формах.
2.В чем преимущества алгоритмического языка перед естественным для записи алгоритмов?
3.Приведите примеры
22 Гладков В.П., Кулютникова Е.А. Пособие по информатике для самообразования.
*цикла, для которого заранее известно количество повторений тела цикла;
*цикла, для которого неизвестно количество повторений тела цикла;
*цикл, который может завершиться по трем причинам.
4.Приведите пример алгоритма, содержащего цикл и ветвление во всех формах.
5.В чем сходство и различие алгоритма и программы? Приведите примеры не менее трех сходств и различий.
6.Представьте в виде алгоритмов решения задач:
*Имеется 12 литров жидкости. Нужно разделить ее поровну с помощью двух пустых сосудов емкостью 8 и 5 литров.
*Имеются две линейки. На одной отмечен отрезок длиной 7 см, на другой - 5 см. Как, пользуясь для измерений только данными линейками, нанести на них сантиметровые деления?
*Есть двое песочных часов: на 3 минуты и на 8 минут. Как с их помощью отмерить ровно 7 минут?
*Как, имея два сосуда, емкостью 5 и 9 литров, набрать из водоема ровно 3 л воды?
*Имеется 9 кг крупы и гири в 50 г и 200 г. Как отмерить в три приема на чашечных весах 2 кг крупы? Как называется такой алгоритм?
*Имеются три сосуда, емкостью 8, 5 и 3 литра. Первый из них наполнен водой. Как разлить воду в два из этих сосудов так, чтобы в каждом было по 4 литра?
*К владельцу бакалейного магазина пришли 10 покупателей, каждый из которых хотел купить двухфунтовый пакет сахара. Утром в магазин привезли двадцатифунтовый мешок сахара. Но бакалейщик еще не успел расфасовать его, потому что у него были только пяти- и девятифунтовые гирьки. Один из покупателей, потеряв терпение, показал бакалейщику самый быстрый способ расфасовки сахара с помощью этих 2 гирь. Как он это сделал?
*Идея устроить в замке костюмированный бал казалась очень романтичной - до тех пор, пока не был поднят мост и 11 дам и 2 кавалера не остались по ту сторону рва, заполненного водой и окружающего замок. Все остальные уже ушли, и некому было им помочь. Потом им удалось найти маленькую лодку, но она могла перевезти за 1 раз только 1 даму (а дамы были в пышных кринолинах) или 2 кавалеров. Как же им всем удалось пересечь ров и не промокнуть?
*Счастливчик Джим и два его приятеля очень спешили - приближалась погоня, а им надо было поделить 9 с виду одинаковых золотых слитков, которые они украли. Джим знал, что один из слитков тяжелее остальных. Достав маленькие весы с чашками, и взвесив слитки всего один раз, он сразу понял, какой это слиток. Как он это сделал?
*Для этой головоломки нужно 80 мелких предметов, например орешки. Вы с товарищем по очереди берете орешки. Выигрывает тот, кто берет последний орешек. За один раз вы можете взять любое количество орехов (от 1 до 9 включительно), причем это количество может меняться по вашему усмотрению. У этой головоломки есть такое решение, которое поможет вам всегда выиграть. Так какое же это решение?
ИСПОЛНИТЕЛИ. КОМПЬЮТЕР - УНИВЕРСАЛЬНЫЙ ИСПОЛНИТЕЛЬ
Исполнитель - это человек, организация или техническое устройство, умеющие исполнять набор команд и совершать ряд проверок.
Эти команды и проверки называются системой команд исполнителя (СКИ). Команда обычно состоит из указания данных, которые нужно обработать, и приказа,
как это сделать. Результатом выполнения команды являются обработанные данные, изменение состояния окружающей среды или изменение внутреннего состояния исполнителя. С помощью проверок определяют состояние окружающей среды или
