
-
Система 1, 2 называется совместимой, если она имеет хотябы одно решение. В противном случае она называется несовместимой.
-
Если решение единственно, то её называют определённой.
-
Если решений множество, то её называют неопределённой.
-
Теорема совместимости Кронекера – Капелли.
-
Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
-
1. Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А к А* не изменяют ранга.
-
-
-
-
Правило Крамера в матричной форме.
-
Пусть дана система
 вида
вида
-

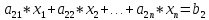




Если в системе 1
 ,
то есть матрица
,
то есть матрица
 ,
то система 1 имеет, и притом единственное,
решение.
,
то система 1 имеет, и притом единственное,
решение.
 ,
или в компонентной
записи:
,
или в компонентной
записи:
 ,
где
,
где
 определитель,
получаемый из определителя
определитель,
получаемый из определителя
 заменой
заменой
 столбца на столбец свободных членов.
столбца на столбец свободных членов.
-
Матричная форма:

Билет 28. Различные подходы к понятию определителя. Свойства определителя.
-
Методы вычисления определителя:
-
Общая формула:
-

Вычисление определителя идет по произвольной строке или столбцу.
-
Определитель второго порядка рассчитывается следующим образом: определитель есть разности произведений элементов главной и побочной диагоналей.
-
Определитель третьего порядка рассчитывается по общей формуле или по правилу треугольника.
-
Правило треугольника
-
Определитель равен алгебраической сумме произведений элементов, расположенных на главной и побочной диагоналях и в вершинах треугольников с основаниями параллельными диагоналям. Произведения элементов, расположенных на побочной диагонали и в вершинах треугольников с основаниями параллельными ей, берутся со знаком минус.
-
Свойства определителя:
-
Определитель не меняется при транспонировании. Это означает, что определитель матрицы равен определителю транспонированной матрицы (матрицы, в которой строки заменены соответствующими столбцами).
-
Если одна из строк (один из столбцов) определителя состоит из нулей, то определитель равен нулю.
-
От перестановки двух строк (столбцов) определитель меняет свой знак.
-
Определитель, содержащий две одинаковые строки(два одинаковых столбцы), равен нулю.
-
Если все элементы некоторой строки (некоторого столбца) умножить на некое число, то сам определитель умножится на это число.
-
Определитель, содержащий две пропорциональные строки (стоблца), равен нулю.
-
Если одна из строк (один из столбцов) определителя есть линейная комбинация его других строк (столбцов), то определить равен нулю.
-
Определитель не меняется, если к одной из его строк (столбцов) прибавляется любая линейная комбинация других строк (столбцов).
-
Если все элементы i-й строки (столбца) определителя n-го порядка представлен в виде суммы двух слагаемых:
 ,
то определитель равен сумме двух
определителей, у которых все строки
(столбцы), кроме i-й, - такие же, как и в
заданом определителе, а i-я строка
(столбец) в одном из слагаемых состоит
из элементов
,
то определитель равен сумме двух
определителей, у которых все строки
(столбцы), кроме i-й, - такие же, как и в
заданом определителе, а i-я строка
(столбец) в одном из слагаемых состоит
из элементов
 ,
в другом - из элементов
,
в другом - из элементов

Билет 29. Общая теория и теорема о структуре общего решения однородной системы. Линейное пространство решений и его размерность.
|| Однородная система – это система с нулевыми свободными членами.

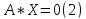
-
Теорема: система 1 и 2 имеет единственное нулевое решение
 тогда и только тогда, когда ранг матрицы
коэффициентов равен числу неизвестных.
тогда и только тогда, когда ранг матрицы
коэффициентов равен числу неизвестных. -
Вопрос о совместности системы не вызывает сомнения, если:
-
-
Доказать, что решение единственно
-

-
РАЗУЗНАТЬ!!!!!

-






Для
исследования
 докажем
следующую теорему.
докажем
следующую теорему.
-
Теорема о пространстве решений однородной системы:
Решение однородной
линейной системы 1,
2 образует линейное
пространство
 ,
являющееся подпространством
,
являющееся подпространством
 и его размерность равна
и его размерность равна
 ,
где
,
где
 - ранг матрицы коэффициентов системы.
- ранг матрицы коэффициентов системы.
-
Докажем замкнутость



-
УТОЧНИТЬ!!!!!!!!!!!! Для того, чтобы найти
 пространства, пусть
пространства, пусть





Билет 30. Теорема о структуре общего решения линейной неоднородной системы. Примеры.
-
Структура общего решения неоднородной линейной системы
-
AX=B (1)
-
AX=0 (2)
-
Разность любых двух решений системы 1 есть решение системы 2.

Общее решение неоднородной линейной системы.



-
Пример:

Билет 31. Собственные векторы и числа линейных преобразований, их свойства, преобразования простой структуры.
Собственные значения и собственные векторы линейного преобразования
-
|| Ненулевой вектор из
 называется собственным вектором
преобразования
называется собственным вектором
преобразования
 ,
если образ
,
если образ
 под действием
под действием

Примеры


-
Для поиска собственных векторов перейдём от преобразования к их матрицам


Для
того чтобы система 1 имела ненулевое
решение, требуется

-
Характеристическое уравнение:

Это уравнение называется
характеристическим уравнением, а его
левая часть – характеристическим
многочленом линейного преобразования

Характеристический многочлен не зависит от выбора базиса
-
Теорема: Для того, чтобы действительное число λ являлось собственным значением линейного оператора, необходимо и достаточно, чтобы оно было корнем характеристического уравнения этого оператора


-
Свойства. Пусть A — линейный оператор, действующий в n-мерном линейном пространстве, λi— собственное значение оператора A, а
 — соответствующий собственный вектор:
A(
— соответствующий собственный вектор:
A( )
=
)
= ,
,
 ≠ 0.
≠ 0.-
Если

-
Если

-
Собственные значения
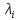 являются
корнями характеристического уравнения.
являются
корнями характеристического уравнения. -
Оператор
 имеет не более
имеет не более
 различных собственных значений
различных собственных значений -
Собственные значения матрицы
 совпадают
совпадают -
Если матрица
 обратима, то все её собственные значения
отличны от нуля
обратима, то все её собственные значения
отличны от нуля
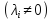 ;
при этом собственными значениями
обратной матрицы
;
при этом собственными значениями
обратной матрицы
 являются числа
являются числа ,
а соответствующие собственные векторы
совпадают.
,
а соответствующие собственные векторы
совпадают. -
Если число
 — собственное значение матрицы
— собственное значение матрицы
 ,
то собственным значением матрицы
,
то собственным значением матрицы
 является число
является число
 ,
а соответствующие собственные векторы
совпадают.
,
а соответствующие собственные векторы
совпадают. -
Собственный вектор, отвечающий собственному значению
 ,
является ненулевым решением линейной
однородной системы
,
является ненулевым решением линейной
однородной системы

-
Собственные векторы, отвечающие различным собственным значениям, линейно независимы.
-
Если линейный оператор
 имеет
имеет
 различных собственных значений, то
соответствующие собственные векторы
образуют базис пространства
различных собственных значений, то
соответствующие собственные векторы
образуют базис пространства
 ,
который называется собственным базисом
линейного оператора.
,
который называется собственным базисом
линейного оператора. -
Собственные векторы, отвечающие различным собственным значениям, ортогональны.
-
Билет 33. Квадратичные формы, их матрицы, привидение к каноническому виду.
Определение квадратичной формы.
-
|| квадратичная форма переменных


 .
.

 значения и
значения и
 ,
то квадратичная форма называется
действительной.
,
то квадратичная форма называется
действительной.
-
Матричная запись квадратичной формы

Её ранг равен рангу
квадратичной формы. Квадратичная форма
называется невырожденной, если

Главные миноры матрицы называются главными минорами квадратичной формы
-
в пространстве
 квадратичную форму можно записать в
виде
квадратичную форму можно записать в
виде
 координатный столбец вектора
координатный столбец вектора

-
в пространстве
 квадратичную форму можно представить
в виде
квадратичную форму можно представить
в виде
 линейный самосопряженный оператор,
матрица которого в некотором
ортонормированном базисе равна
линейный самосопряженный оператор,
матрица которого в некотором
ортонормированном базисе равна
 .
.
Квадратичная
форма называется канонической, если
все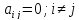 то
есть
то
есть
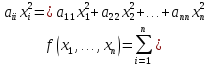
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.
-
Ортогональное преобразование пространства

 ,
где
,
где
 –
собственные значения матрицыА
–
собственные значения матрицыА
-
Метод Лагранжа - последовательное выделение полных квадратов. Например, если


Затем подобную процедуру
проделывают с квадратичной формой и
т. д. Если в квадратичной форме все
и
т. д. Если в квадратичной форме все ,
но есть
,
но есть
 то после предварительного преобразования
дело сводится к рассмотренной процедуре.
Так, если, например,
то после предварительного преобразования
дело сводится к рассмотренной процедуре.
Так, если, например,
 ,
то полагаем
,
то полагаем
 ;
;
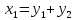 ;
;

-
Метод Якоби (в случае, когда все главные миноры
 квадратичной
формы отличны от нуля):
квадратичной
формы отличны от нуля):

Билет 34. Знакоопределение квадратичной формы, критерии знакоопределения.
-
Знакоопределение квадратичной формы

-
Знаконеопределена если существуют такие столбцы x и y, что:



-
Положительно (отрицательно) определена если :


-
Неотрицательна (не положительна) если:
 ,
для любого столбца х, причем существует
ненулевой столбец для которого
,
для любого столбца х, причем существует
ненулевой столбец для которого

-
Критерии знакоопределения:
Тип квадратичной формы зависит только от множества значений, которые она принимает, но не зависит от переменных, в которых она записана. Поэтому, представив квадратичную форму в каноническом виде, сразу получаем следующие критерии для типа квадратичной формы в зависимости от множества собственных значений ее матрицы.
|
Тип квадратичной формы |
Множество собственных значений |
|
Положительно определенная (Для всех
|
Все собственные значения положительны
|
|
Отрицательно определенная (Для всех
|
Все собственные значения отрицательны
|
|
Знакопеременная (Существуют x
и y
для которых: |
Есть собственные значения разных знаков Существуют
|
|
Вырожденная (Существуют
|
Есть нулевое собственное значение Существуют
|




 )
)
 )
)
 )
)
 для
которых
для
которых
 )
)