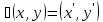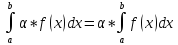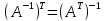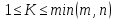• 

• Теорема:

  • 

• (если спросит) Замечание:

Изучать геометрические свойства, связанные с длинами и углами на самом простом пространстве

Билет 22. Линейные операторы. Примеры линейных операторов. Ранг. Ядро. Вырожденные и невырожденные операторы.

Роль функций на линейных пространствах отведена линейным операторам.

• Линейным оператором 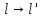называется такое отображение , что для , и выполняются следующие условия

  • 

• Примеры линейных операторов

  • Если

  • Если

  • Изоморфизм является линейным оператором

  • 

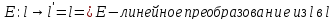
  • Пусть

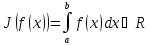
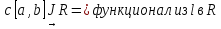
• Линейность следует из свойств определённого интеграла

  • 

  • 

• Та же фигня с производными

• Простейшие свойства линейных операторов

  • Образ нуля равен нулю

  • Образ линейной комбинации есть линейная комбинация образов

  • Линейный оператор сохраняет линейную зависимость и линейную независимость систем векторов.

• Понятие ранга и дефекта линейных операторов

  • || Назовём областью значений линейного оператора множество

• || Ядро линейного оператора представляет собой подмножество

  • 

• || Назовём размерность пространства образов рангом линейного оператора

Размерность ядра – дефект

• Пример. Тождественное линейное преобразование, действующее из

• Понятие невырожденных линейных преобразований.

  • || Назовем линейное преобразование называется невырожденным, если его ядро состоит только из нулевого элемента

    • Пример.

  • ! Если невырожденное, то дефект А равен нулю.

  • Свойство 1: для любого для невырожденного преобразования 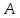существует единственный прообраз.

    • Докажем от противного

• Свойство 2: произведение конечного числа линейных невырожденных преобразований невырождено.

  • Докажем свойство 2 для двух сомножителей.

    • 

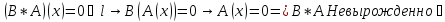
• ! Замечание: для суммы свойство 2 неверно

Билет 23. Матрицы линейных операторов. Действия с линейными операторами и их матрицами.

Покажем, что общим способом задания линейных операторов является задание с помощью матрицы.

• Пусть дано

• Вывод: Линейное преобразование задано выражением 3 однозначно и полностью описано матрицей

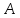
• (писать если спросит) Матричный смысл

  • 1.

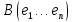
• 2.

• Операции над матрицами

  • Пусть дано отображение

  • Тогда введём новое отображение

  • Составим матрицу

    • Складывать по формуле 1 можно только однотипные матрицы

  • 

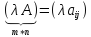
  • Однотипные матрицы будут образовывать линейные пространства по отношению к введённым операциям сложения и умножения на число

• Умножения матриц

  • Пусть даны

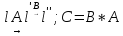
• Из определения умножения операторов следует то, что можно перемножить согласованные матрицы , чтобы у левой столбцов было столько, сколько строк во второй.

Билет 24. Обратные преобразования, обратные матрицы.

• Всякая невырожденная матрица имеет обратную.

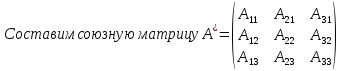
• Свойства обратной матрицы

  • 

  • 

  • 

• Обратное преобразование.

  • Свойство 1: для любого для невырожденного преобразования существует единственный прообраз.

    • Докажем от противного

Пусть

Тогда по свойству 1:

Для всех :

- обратное линейное преобразование A

Тогда:

Билет 26. Ранг матрицы и способы его нахождения. Теорема о базисном миноре.

• Ранг матрицы

• 

Рангом матрица A называют число R которое равно максимальному порядку ее минором отличных от 0.

Ранг нулевой матрицы равен 0. Для определения ранга используется следующие преобразования, называемые элементарными:

• Умножение столбца на число отличное от 0

• Сложение любых столбцов

• Перемещение любых двух столбцов

• Аналогичные преобразования для строк

! Элементарные преобразования не меняют ранга матрицы.

• Теорема о базисном миноре

Определитель, полученный из матрицы K*K называется минором матрицы.

Базисным называется минор матрицы отличной от 0, порядок которого равен рангу матрицы, тогда все строки и столбцы этого минора называются базисными.

• Теорема: Базисные столбцы линейно независимы, а любой столбец – линейная комбинация базисных.

! Аналогичная теорема и для строк.

Предположим, что базисным является левый угловой минор.

(1)

Докажем линейную независимость первых r столбцов от противного.

Пусть – линейно зависимы, тогда один из них есть линейная комбинация остальных. , что противоречит 1 → Столбцы линейно независимы.

• Докажем, что любой столбец – линейная комбинация первых r мтолбцов.

(2)

1. 

(3)

2. 

Возьмем произвольную i-ую строку и приведем ее вместе с j-тым

столбцом к следующему определению:

(4)

• Докажем, что

1. 

2. 

Для доказательства соотношения 2 разложим по строке:

(5)

– для всех одинаковы

(6)

Билет 27. Теорема о совместимости линейной системы. Правило Крамера в матричной форме.