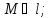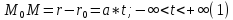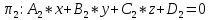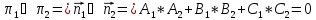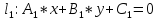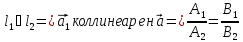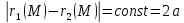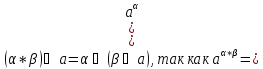Билет 1. Векторы. Линейные операции над векторами и их свойства.
-
||Вектор – это направленный отрезок.
-
||Коллинеарные векторы – это векторы, лежащие на одной или параллельных прямых.
-
а ↑↑b a ↑↓b
-
-
||Компланарные векторы – это три (или более) вектора, лежащие в одной плоскости
-
Операции:
-
Сложение (правила треугольника и параллелограмма)
-
Умножение на число
-
-
|| Пусть даны два вектора aи b. Поcтроим равные им векторы ABи BC. Тогда вектор ACназывается суммой векторов aи bи обозначается

-
Свойства сложения
-

-

-

-
 a
+ (-a) = 0
a
+ (-a) = 0
-
-
|| Произведением вектора aна вещественное число αназывается векторb, удовлетворяющий следующим условиям:
-
(Если же α=0, то из первого условия следует, что b=0.)
Произведение вектора а на число α обозначается α*a
-
Свойства умножения
-


-
Для любых векторов a, bиc и любых чисел
 выполненно:
выполненно: -
-
||Вектор (-1)*a обозначается –a. Разность векторов aи bназывается суммой векторов aи –b. Она обозначается a-b.
Билет 2. Базис, теорема разложения вектора по базису, координаты вектора.
-
|| Базисом в векторном пространстве называется упорядоченная линейно независимая система векторов такая, что любой вектор этого пространства по ней раскладывается.
-
В нулевом пространстве базиса не существует.
-
В одномерном пространстве (на прямой линии) базис состоит из одного ненулевого вектора
-
В двумерном пространстве (на плоскости) базис состоит из упорядоченной пары некомпланарных векторов.
-
В трёхмерном пространстве базис – упорядоченная тройка некомпланарных векторов.
-
-
||Система векторов называется линейно независимой, если нулевой вектор раскладывается по ней единственным образом.
-
|| Три (или более) вектора называются компланарными, если они лежат в одной плоскости.
-
Базис называется правым, если тройка правая, и наоборот.
-
|| Ортонормированным правым базисом называется базис, у которого
-
Векторы единичной длины
-
Попарно ортогональны (перпендикулярны)
-
-
ТЕОРЕМА О РАЗЛОЖЕНИИ ПО БАЗИСУ:
-
Всякий вектор однозначно разлагается по ортонормированному базису.
-
-
Разложение вектора по базису (Письменный с. 35).
-
||Так как векторы базиса линейно независимы, коэффициенты разложения по базису для каждого вектора пространства определены однозначно. Они называются компонентами или координатами вектора в этом базисе.
-
При умножении вектора на число все его компоненты увеличиваются на это число. При сложении векторов складываются их соответствующие компоненты
Билет 3. Действия над векторами в координатах, деление отрезка в заданном отношении.
Действия над векторами с заданными проекциями.
-
Пусть векторы
 заданы
своими проекциями на оси координат
заданы
своими проекциями на оси координат
 или, что тоже самое:
или, что тоже самое:
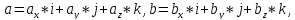
-
Линейные операции над векторами
-
Так как линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:
-
-
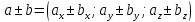
-
Доказательство:
Если
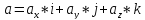 и
и
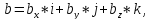 то
то

-
При умножении вектора на скаляр координаты вектора умножаются на этот скаляр
-
Доказательство:
Если
 ,
то
,
то

Деление отрезка в заданном отношении.
-
Если точка
 лежит на прямой, проходящей через две
данные точки
лежит на прямой, проходящей через две
данные точки
 ,
и дано отношение
,
и дано отношение
 ,
в котором точка М делит отрезок
,
в котором точка М делит отрезок
 ,
то координаты точки М определяются по
формулам:
,
то координаты точки М определяются по
формулам:

-
Доказательство:
Найдём координаты точки М на отрезке
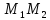 ,
которая делит этот отрезок:
,
которая делит этот отрезок:
 .
.
Это условие можно переписать в виде
 .
разложим обе части по базису:
.
разложим обе части по базису:


Билет 4. Скалярное произведение векторов, свойства, вычисление в прямоугольных декартовых координатах.
-
|| Скалярным произведением векторов называется число, равное произведению модулей этих векторов на косинус угла между ними. Обозначается символом ab
Скалярное произведение можно так же выразить формулой

-
ab>0 если
 –
острый
–
острый -
ab<0 если
 - тупой
- тупой -
ab=0 если векторы a и b перпендикулярны
Скалярное произведение aa
называется скалярным квадратом и
обозначается символом
 .
Из формулы
.
Из формулы
 следует, что каждый скалярный квадрат
вектора равен квадрату его модуля:
следует, что каждый скалярный квадрат
вектора равен квадрату его модуля:
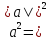 .
.
-
Свойства скалярного произведения:
-
-
Если векторы a и b заданы своими координатами:
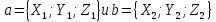
То их произведение высчитывается по формуле:
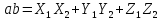
Угол
 находится из формулы
находится из формулы
 или
в координатах:
или
в координатах:
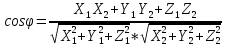
Билет 5. Векторное произведение векторов, свойства и вычисление в прямоугольных декартовых координатах
-
Векторным произведением
 называется такой третий вектор, который
называется такой третий вектор, который-
Имеет длину, равную произведению длин векторов на

-
Вектор направлен перпендикулярно обоим сомножителям
-
Направление вектора [ab] соответствует «правилу правой руки». Это означает, что если векторы a, b и [ab] приведены к общему началу, большой палец правой руки направлен по первому сомножителю, а указательный – по второму, то средний палец будет направлен по вектору [ab].
-
-
Геометрические свойства векторного произведения
-
Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
-
Модуль векторного произведения [ab] равняется площади параллелограмма, построенного на приведённых к общему началу векторах a и b.
-
-
Алгебраические свойства векторного произведения
-
-
Векторное произведение двух векторов удобнее всего находить по формуле
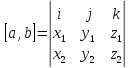
-
Доказательство:

Билет 6. Смешанное произведение векторов, свойства, вычисление в прямоугольных декартовых координатах.
Смешанным произведением трех векторов a,b,c называется число равное векторному произведению [ab], скалярно умноженное на вектор c. И обозначается [ab]c.

Смешанное произведение векторов a,b,c равно объему параллелепипеда, построенного на векторах а, b, с, взятому со знаком плюс, если тройка a,b,c правая, и со знаком минус, если эта тройка левая. Если векторы а, b, с компланарны (и только в этом случае), смешанное произведение abc равно нулю; иначе говоря, равенство

есть необходимое и достаточное условие компланарной векторов.
Свойства:
-
Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е.
 .
.
-
Смешанное произведение не меняется при перемене местами векторного и скалярного произведений, т.е.

-
Смешанное произведение меняет знак при перемене местами любых двух сомножителей, т.е.
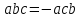
-
Смешанное произведение равно нулю только тогда когда векторы компланарны.
Вычисление в прямоугольных декартовых координатах:
Пусть заданы векторы
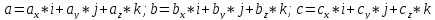 .
Найдем их смешанное произведение,
используя выражения в координатах для
векторного и скалярного произведений.
.
Найдем их смешанное произведение,
используя выражения в координатах для
векторного и скалярного произведений.

Полученную формулу можно записать короче:

Билет 7. Уравнения линий на плоскости и поверхностей в пространстве. Теорема о геометрическом смысле уравнении первой степени с 2 и 3 неизвестными.
-
|| Уравнение
 называется уравнением линии L
(в заданной системе координат), если
этому уравнению удовлетворяют координаты
x
и y
любой точки, лежащей на линии L,
и не удовлетворяют координаты никакой
точки, не лежащей на этой линии.
называется уравнением линии L
(в заданной системе координат), если
этому уравнению удовлетворяют координаты
x
и y
любой точки, лежащей на линии L,
и не удовлетворяют координаты никакой
точки, не лежащей на этой линии. -
Из определения следует, что линия L представляет собой множество всех тех точек плоскости, координаты которых удовлетворяют уравнению
 .
Это уравнение задаёт линию L.
.
Это уравнение задаёт линию L. -
Линия L может определяться уравнением вида
 ,
где
,
где
 - полярные координаты точки.
- полярные координаты точки. -
|| Уравнение
 является уравнением поверхности S
в заданной системе координат, если ему
удовлетворяют координаты любой точки
является уравнением поверхности S
в заданной системе координат, если ему
удовлетворяют координаты любой точки
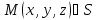 ,
и не удовлетворяют координаты никакой
точки, не лежащей на этой поверхности.
,
и не удовлетворяют координаты никакой
точки, не лежащей на этой поверхности. -
Линию в пространстве можно рассматривать как пересечение двух поверхностей, то есть как множество точек, находящихся одновременно на двух поверхностях, и соответственно этому определять линию заданием двух уравнений.

-
Теорема о геометрическом смысле линейного уравнения с тремя неизвестными.
-
Пусть давно уравнение

-
 - прямоугольные
декартовые координаты в трёхмерном
пространстве.
- прямоугольные
декартовые координаты в трёхмерном
пространстве.

Уравнение 1 с условием на коэффициенты при неизвестных 2 задаёт в прямоугольных декартовых координатах плоскость π.
-
Пусть
 ,
тогда
,
тогда

-

-


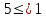
Выясним геометрический смысл 5




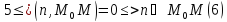



Вывод: все точки M,
координаты которых удовлетворяют 5,
принадлежат плоскости π,
которая перпендикулярна нормальному
вектору n
и содержит точку

Аналогично с двумя неизвестными
Билет 8. Различные типы уравнений прямой на плоскости и плоскости в пространстве.
-
Общее уравнение прямой
Рассмотрим уравнение первой степени
относительно x и y
в общем виде ,
где А, В, С – произвольные числа, причем
А и В не равны нулю одновременно. Покажем,
что приведенное выше уравнение –
уравнение прямой линии. Возможны 2
случая.
,
где А, В, С – произвольные числа, причем
А и В не равны нулю одновременно. Покажем,
что приведенное выше уравнение –
уравнение прямой линии. Возможны 2
случая.
-
Если
 ,
то уравнение имеет вид
,
то уравнение имеет вид
 ,
причем
,
причем
 ,
отсюда
,
отсюда
 .
Это есть уравнение прямой, параллельной
оси Oy и проходящей через
точку
.
Это есть уравнение прямой, параллельной
оси Oy и проходящей через
точку

-
Если
 ,
то
,
то
 .
Это уравнение прямой с угловым
коэффициентом
.
Это уравнение прямой с угловым
коэффициентом
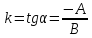
-
Частные случаи уравнения прямой:
-
Если
 ,
то
,
то
 .
Прямая параллельна оси Оx
.
Прямая параллельна оси Оx -
ЕслиВ = 0, то
 .
Прямая параллельна оси Oy
.
Прямая параллельна оси Oy -
Если
 ,
то получаем
,
то получаем
 ,
прямая проходит через начало координат.
,
прямая проходит через начало координат.
-
-
Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая проходит через точку М и ее направление характеризуется угловым
коэффициентом к. Уравнение этой прямой
можно записать в виде
и ее направление характеризуется угловым
коэффициентом к. Уравнение этой прямой
можно записать в виде
 ,
где b – пока неизвестная
величина. Так как прямая проходит через
точку М
,
где b – пока неизвестная
величина. Так как прямая проходит через
точку М ,
то координаты точки удовлетворяют
уравнению
,
то координаты точки удовлетворяют
уравнению
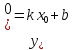 ,
отсюда
,
отсюда
 .
Подставив значение b в
уравнение
.
Подставив значение b в
уравнение
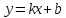 ,
получим искомое уравнение
,
получим искомое уравнение

-
Уравнение прямой, проходящей через 2 точки.
Пусть прямая проходит через точки
 .
Уравнение прямой проходящей через точку
.
Уравнение прямой проходящей через точку
 имеет вид
имеет вид
 ,
где к- пока неизвестный коэффициент.
Так как прямая проходит через точку
,
где к- пока неизвестный коэффициент.
Так как прямая проходит через точку
 ,
то координаты точки должны удовлетворять
уравнению
,
то координаты точки должны удовлетворять
уравнению
 .
Отсюда находим
.
Отсюда находим
 ,
подставляя k в уравнение
,
подставляя k в уравнение
 получим уравнение прямой проходящей
через точки
получим уравнение прямой проходящей
через точки
 .
.

Предполагается что
 .
Если
.
Если
 ,
то прямая параллельна оси ординат, если
же
,
то прямая параллельна оси ординат, если
же
 ,
то прямая параллельна оси абсцисс.
,
то прямая параллельна оси абсцисс.
-
Уравнение прямой в отрезках
Пусть прямая пересекает ось ОХ
в точке М1(a;0),
а ось ОУв точке М2(0;b).
В этом случае уравнение примет вид:
 ,
т.е.
,
т.е.
 .
Это уравнение называется уравнением
прямой в отрезках так как числа а и b
указывают, какие отрезки отсекает прямая
на осях координат.
.
Это уравнение называется уравнением
прямой в отрезках так как числа а и b
указывают, какие отрезки отсекает прямая
на осях координат.
-
Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору
Найдем уравнение прямой проходящей
через заданную точку М0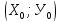 и перпендикулярно некоторому вектору
n(А;В). Возьмем на прямой
произвольную точку М(Х;У) и рассмотрим
вектор
и перпендикулярно некоторому вектору
n(А;В). Возьмем на прямой
произвольную точку М(Х;У) и рассмотрим
вектор
 поскольку векторы
поскольку векторы
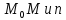 перпендикулярны их скалярное произведение
равно 0.
перпендикулярны их скалярное произведение
равно 0.
 .
.
-
Уравнение плоскости, проходящей через данную точку , перпендикулярно данному вектору
Пусть в пространстве OXYZ
плоскость Qзадана
точкой M0(X0;Y0;Z0)
и вектором n(A;B;C)
перпендикулярным к этой плоскости.
Возьмем на плоскости точку M(X;Y;Z).
Построим вектор M0M=(X-X0;Y-Y0;Z-Z0).
Вектора M0Mиn
перпендикулярны и их скалярное
произведение равно 0. .
.
-
Общее уравнение плоскости
Рассмотрим общее уравнение первой степени с тремя переменными xyz
 ,
предполагая, что один из коэффициентов
неравен 0. НапримерВ.
,
предполагая, что один из коэффициентов
неравен 0. НапримерВ.
Получим
-
Уравнение плоскости, проходящей через 3 точки
Найдем уравнение плоскости. Проходящей
через точки
 ,
, не лежащих на одной прямой. Возьмем на
плоскости точку M(X;Y;Z)
и соответственные вектора:
M1M=(X-X1;Y-Y1;Z-Z1),
M2M=(X-X2;Y-Y2;Z-Z2),
M3M=(X-X3;Y-Y3;Z-Z3)
из условия компланарной получаем:
M1M*M2M*M3M=0(смешанное
произведение равно 0).
не лежащих на одной прямой. Возьмем на
плоскости точку M(X;Y;Z)
и соответственные вектора:
M1M=(X-X1;Y-Y1;Z-Z1),
M2M=(X-X2;Y-Y2;Z-Z2),
M3M=(X-X3;Y-Y3;Z-Z3)
из условия компланарной получаем:
M1M*M2M*M3M=0(смешанное
произведение равно 0).

-
Уравнение плоскости в отрезках
Пусть плоскость отсекает на осях отрезки
a, b,
c и проходит через
точки A(a;0;0),
B(0;b;0),
C(0;0;c)
подставляем координаты точек в уравнение
и получаем:

Найдем определитель
 такое уравнение называетсяуравнением
плоскости в отрезках.
такое уравнение называетсяуравнением
плоскости в отрезках.
-
Нормальное уравнение плоскости
Положение плоскости Q
вполне определяется заданием единичного
вектора е, имеющего направление
перпендикуляра ОК, опущенного на
плоскость из начала координат, и длиной
p этого перпендикуляра.
Пусть ОК =р , аα,β,γ – углы, образованные
единичным вектором е с осямиОх,
Оу, Oz. Тогда
 .
Возьмем на плоскости произвольную точку
М(х; у; z) и
соединим её с началом координат. Получим
вектор
.
Возьмем на плоскости произвольную точку
М(х; у; z) и
соединим её с началом координат. Получим
вектор .
Проекция радиус вектора r
на направление вектора е равна
.
Проекция радиус вектора r
на направление вектора е равна
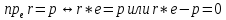 .
Это уравнение называется нормальным
уравнением плоскости в векторной форме.
Зная координаты r
и руравнение приобретает вид
.
Это уравнение называется нормальным
уравнением плоскости в векторной форме.
Зная координаты r
и руравнение приобретает вид
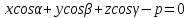 это
нормальное уравнение плоскости в
координатной форме.
это
нормальное уравнение плоскости в
координатной форме.
Билет 9. Различные типы уравнений прямой в пространстве, их взаимосвязь.
|
|
(Векторное параметрическое уравнение прямой)
|
-
Исключим из (2) t

(коэффициенты в знаменателе могут равняться нулю.)
-
Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей. Рассмотрим систему уравнений
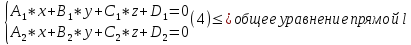
-
Каждое из уравнений этой системы определяет плоскость. Если плоскости не параллельны (координаты векторов
 не пропорциональны), то система 4
определяет прямую
не пропорциональны), то система 4
определяет прямую
 как геометрическое место точек
пространства, координаты которых
удовлетворяют каждому из уравнений
системы
как геометрическое место точек
пространства, координаты которых
удовлетворяют каждому из уравнений
системы -
От общих уравнений можно перейти к каноническим. Координаты точки
 получаем из системы уравнений 4,
придав одной из координат произвольное
значение (например, z=0).
получаем из системы уравнений 4,
придав одной из координат произвольное
значение (например, z=0). -
Так как прямая перпендикулярна векторам
 ,
то за направляющий вектор
,
то за направляющий вектор
 прямой
прямой
 можно принять векторное произведение
можно принять векторное произведение

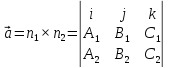


Замечание: все рассмотренные типы уравнений прямой переносятся на случай прямой на плоскости исключением третьих координат векторов.
Билет 10. Определение расстояния от точки до плоскости и до прямой на плоскости, до прямой в пространстве. Определение расстояния между скрещивающимися прямыми в пространстве.
-
Определение расстояния от точки до плоскости
-
Пусть задана точка
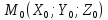 и плоскость Q своим
уравнением
и плоскость Q своим
уравнением
-
 .
Расстояние d от точки
до плоскости рассчитывается по формуле:
.
Расстояние d от точки
до плоскости рассчитывается по формуле:

-
Расстояние d равно
модулю проекции вектора
 ,
где
,
где
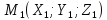 – произвольная точка плоскости Q,
направление нормального вектора
– произвольная точка плоскости Q,
направление нормального вектора
 .
Следовательно,
.
Следовательно,

А так как точка
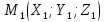 принадлежит плоскости Q,
то
принадлежит плоскости Q,
то
 отсюда
отсюда
 .
Поэтому
.
Поэтому

-
Если плоскость задана уравнением
 ,
то
,
то

-
Определение расстояния от точки до прямой на плоскости
Пусть заданы прямая L
уравнением
 и точка
и точка
 .
Расстояние d от
точки до прямой равно модулю проекции
вектора
.
Расстояние d от
точки до прямой равно модулю проекции
вектора
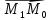 ,
где
,
где
 – произвольная точка на прямой,
направление нормального вектора
– произвольная точка на прямой,
направление нормального вектора
 .
Следовательно
.
Следовательно

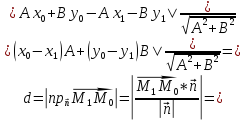
А так как точка
 принадлежит прямой L,
то
принадлежит прямой L,
то
 отсюда
отсюда
 .
Поэтому
.
Поэтому

-
Определение расстояния между скрещивающимися прямыми
Пусть
 – скрещивающиеся прямые. Натянем на
них параллелепипед, тогда расстояние
будет равно объему параллелепипеда
деленному на его основание и равно его
высоте:
– скрещивающиеся прямые. Натянем на
них параллелепипед, тогда расстояние
будет равно объему параллелепипеда
деленному на его основание и равно его
высоте:


Билет 11. Определение углов между плоскостями, между прямыми на плоскости и в пространстве, между прямой в пространстве и плоскостью. Условия параллельности и перпендикулярности прямых и плоскостей.
-
Вычисление углов между плоскостями.
-
Пусть заданы 2 плоскости
-
-

-

-
-
Условия параллельности и перпендикулярности плоскостей
-
-
Вычисление углов между прямыми на плоскости
-
Пусть заданы 2 прямые
-
-

-

-
-
Условия параллельности и перпендикулярности прямых на плоскости.
-
-
Вычисление угла между прямыми в пространстве
-
Пусть заданы две прямые
-
-

-

-
-
Условия параллельности и перпендикулярности прямых в пространстве.
-
-
Вычисление угла между прямой и плоскостью в пространстве
-
Пусть заданы прямая и плоскость
-
-

-

-

-
|
|
Билет 12. Кривые 2-го порядка как геометрические места точек на плоскости. Канонические уравнения кривых (вывод одного из них)
-
Линии, которые задаются уравнением вида:
 .
Коэффициенты уравнения – действительные
числа, но по крайней мере одно из чисел
A, B, или C
отлично от нуля. Данное уравнение
определяет на плоскости окружность,
эллипс, гиперболу и параболу.
.
Коэффициенты уравнения – действительные
числа, но по крайней мере одно из чисел
A, B, или C
отлично от нуля. Данное уравнение
определяет на плоскости окружность,
эллипс, гиперболу и параболу. -
Уравнения кривых второго порядка:
-
Окружность:

-
Эллипс:
Обозначим фокусы через расстояние между ними через 2с, а
сумму расстояний от произвольной точки
эллипса до фокусов – через 2а. по
определению:
расстояние между ними через 2с, а
сумму расстояний от произвольной точки
эллипса до фокусов – через 2а. по
определению:
 .
Для вывода уравнения эллипса выберем
систему координат Оху так, чтобы
фокусы лежали на оси Ох, а начало
координат совпадало с серединой отрезка
.
Для вывода уравнения эллипса выберем
систему координат Оху так, чтобы
фокусы лежали на оси Ох, а начало
координат совпадало с серединой отрезка
 .
Тогда фокусу будут иметь следующие
координаты
.
Тогда фокусу будут иметь следующие
координаты
 и
и
 .
Пусть M(x;
y) – произвольная
точка эллипса. Тогда, согласно определению
эллипса,
.
Пусть M(x;
y) – произвольная
точка эллипса. Тогда, согласно определению
эллипса,
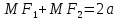 ,
т. е.
,
т. е.
 .
Это по сути и есть уравнение эллипса.
Преобразуем его к более простому виду:
.
Это по сути и есть уравнение эллипса.
Преобразуем его к более простому виду:


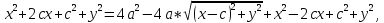



Так как
 ,
то
,
то
 .
Допустим, что
.
Допустим, что
 ,
тогда последнее уравнение примет вид
,
тогда последнее уравнение примет вид
 или
или
 это и есть каноническое уравнение
эллипса
это и есть каноническое уравнение
эллипса
-
Гипербола:

-
Парабола:

Билет 13. Исследование свойств кривых второго порядка по их каноническим уравнениям.
-
ЭЛЛИПС
-
Каноническое уравнение кривой
-
-
Исследование формы эллипса по его уравнению.
-
Параметры
 называются
полуосями эллипса (большой и малой
соответственно).
называются
полуосями эллипса (большой и малой
соответственно). -
Точки

-
Оси симметрии
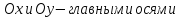
-
Центр симметрии

-
Точки
 ,
называются фокусами эллипса
,
называются фокусами эллипса -
Векторы

-
Числа
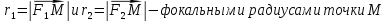 ,
принадлежащей эллипсу.
,
принадлежащей эллипсу. -
-
В частном случае
 фокусы
фокусы
 совпадают с центром, а каноническое
уравнение имеет вид:
совпадают с центром, а каноническое
уравнение имеет вид:

-
Эксцентриситет
-
Директрисы
-
-
-
-
ГИПЕРБОЛА
-
Каноническое уравнение кривой
-
-
Исследование формы гиперболы по её уравнению.
-
Параметры
 называются
полуосями гиперболы
называются
полуосями гиперболы -
Точки

-
Оси симметрии

-
Центр симметрии

-
Прямые
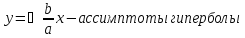
-
Точки

-
Векторы

-
Числа
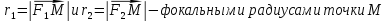 ,
принадлежащей гиперболе.
,
принадлежащей гиперболе. -
-
Эксцентриситет
-
Директрисы
-
-
В частном случае
 ,
гипербола
называется равносторонней; её
эксцентриситет равен
,
гипербола
называется равносторонней; её
эксцентриситет равен
 ,
а угол между асимптотами равен
,
а угол между асимптотами равен

-
-
-
ПАРАБОЛА
-
Каноническое уравнение кривой
-
-
Исследование формы параболы по её уравнению.
-
Число
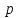 называется параметром параболы
называется параметром параболы -
Точка
 вершина параболы
вершина параболы -
Ось

-
Точка

-
Вектор

-
Число
 - фокальный радиус точки
- фокальный радиус точки
 параболы
параболы -
Директриса
-
-
Билет 14. Директрисы и эксцентриситет кривых второго порядка. Фокальные свойства и общий подход к заданию уравнений кривых второго порядка в полярной системе координат.
-
Директрисы и эксцентриситет
-
Эллипс
-
Эксцентриситет – мера сплюснутости. Если эксцентриситет равен 0, то эллипс = окружность.
 ,
,

-
Директрисы – прямые параллельные главной оси и проходящие на расстоянии
 от центра
от центра
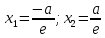
-
-

-
Сумма расстояний от произвольной точки эллипса до фокусов равна 2а
-
Гипербола
-
Эксцентриситет – мера сплюснутости. Если
 ,
то гипербола равносторонняя.
,
то гипербола равносторонняя.
 ,
,
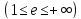
-
Директрисы – прямые перпендикулярные действительной оси и проходящие на расстоянии
 от ее центра
от ее центра
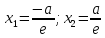
-

-
Модуль разности расстояний от точек гиперболы до фокусов равен 2а
-
Парабола
-
Директриса – прямая перпендикулярная оси и проходящие на расстоянии
 от вершины параболы
от вершины параболы

-
-
Общий подход к заданию уравнений кривых второго порядка в полярной системе координат
Говорят, что на плоскости введена
полярная система координат
 ,
если заданы:
,
если заданы:
-
некоторая точка О, называемая полюсом;
-
некоторый луч и, исходящий из точки О и называемый полярной осью
Полярными координатами точки
 называются два числа: полярный
радиус
называются два числа: полярный
радиус
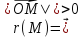 и полярный угол
и полярный угол
 )
— угол, на который следует повернуть
ось u для того,
чтобы ее направление совпало с направлением
вектора
)
— угол, на который следует повернуть
ось u для того,
чтобы ее направление совпало с направлением
вектора
 (при этом, как обычно,
(при этом, как обычно,
 ,
если поворот осуществляется против
часовой стрелки, и
,
если поворот осуществляется против
часовой стрелки, и
 в противном случае). Запись
в противном случае). Запись
 означает, что точка М
имеет полярные координаты r
и φ.
означает, что точка М
имеет полярные координаты r
и φ.
Полярный угол
 имеет бесконечно много возможных
значений (отличающихся друг от друга
на величину вида
имеет бесконечно много возможных
значений (отличающихся друг от друга
на величину вида
 ).
Значение полярного угла, удовлетворяющее
условию
).
Значение полярного угла, удовлетворяющее
условию
 ,
называется главным.
В некоторых случаях главным
значением полярного угла называют
значение φ,
удовлетворяющее условию
,
называется главным.
В некоторых случаях главным
значением полярного угла называют
значение φ,
удовлетворяющее условию

Пусть на плоскости введены правая
декартова прямоугольная система
координат Оху
(т.е. такая, что кратчайший поворот
от оси Ох к
оси Оу происходит
против часовой стрелки) и полярная
система (О;u),
причем полярная ось совпадает с
положительной полуосью абсцисс. Тогда
связь между декартовыми прямоугольными
и полярными координатами произвольной
точки
 дается формулами
дается формулами
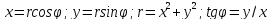
Уравнение кривой в полярных координатах
имеет вид
 или
или
 .
Оно может быть получено либо непосредственно,
исходя из геометрических свойств кривой,
либо переходом к полярным координатам
в уравнении этой кривой, заданном в
декартовых прямоугольных координатах.
.
Оно может быть получено либо непосредственно,
исходя из геометрических свойств кривой,
либо переходом к полярным координатам
в уравнении этой кривой, заданном в
декартовых прямоугольных координатах.
Билет 15. Линейные пространства и подпространства, примеры линейных пространств и подпространств.
Будем строить теорию линейных пространств, не заботясь о природе их элементов, а задавая только операции над ними, да и то не конкретно, а с помощью их свойств (св-в операций).
-
Определение линейного пространства
-
|| линейным пространством называется множество
 с элементами
с элементами
 произвольной природы, для которого:
произвольной природы, для которого:-
Определена операция сложения
-

-
-
Эти операции предполагаются удовлетворяющими следующим 8 аксиомам:
-
 +
+ -

-

-

-
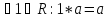
-

-

-
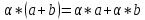
-
-
-
Примеры линейных пространств
-
Для выяснения, является ли конкретное множество с заданными на нём операциями сложения и умножения на число линейным пространством, нужно проверить возможность ввести операции «+» и «*» и справедливость всех 8 аксиом
-
Примеры
-
Множество действительных чисел

-
Множество

-
Множество многочленов в степени, не превышающей n
-
-
-

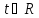

-
Матрицы
-

Билет 16. Линейная зависимость, свойства линейно зависимых и независимых систем векторов в линейном пространстве.
-
 – линейная комбинация в L
(1)
– линейная комбинация в L
(1)-
Назовем 1 тривиальной комбинацией если все коэффициенты обращаются в 0
-
Назовем 1 нетривиальной комбинацией если

-
-
Система векторов линейного пространства называется линейно зависима если существует её нетривиальная комбинация равная нуль-вектору.
-
Система векторов линейного пространства называется линейно независимой если любая из ее линейных комбинаций равна 0 и является тривиальной.
-
Простейшие свойства
-
Теорема 1. Критерий линейной зависимости.
-
Система векторов линейно зависима тогда когда хоть один из ее векторов является линейной комбинацией остальных.
 линейно зависима, тогда:
линейно зависима, тогда:
 ;
(2)
;
(2)

-
Теорема 2. Если подсистема линейно зависима, то и вся система линейно зависима
 -
линейно зависима
-
линейно зависима
 ,
тогда
,
тогда
 (3)
(3)
Из 3 следует, что система линейно
зависима.
-
Теорема 3. Если любая подсистема линейно независима, то и вся система линейно независима.
 -
линейно независима
-
линейно независима
 ,
тогда
,
тогда
 – линейно независима, но тогда вся
система линейно независима
– линейно независима, но тогда вся
система линейно независима
-
Геометрические свойства линейной зависимости
-
Теорема 4. Тройка компланарных векторов
 в
в
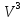 линейно
зависима
линейно
зависима
-
 предположим,
что
предположим,
что
 противном случае для
противном случае для
 ,
тогда пара векторов будет линейно
зависима, а значит и вся система будет
линейно зависима.
,
тогда пара векторов будет линейно
зависима, а значит и вся система будет
линейно зависима.
Если не компланарна, то по теореме о разложении по базису
 и тогда система будет линейно зависима.
и тогда система будет линейно зависима.
-
Теорема 5. Любые 4 вектора в
 линейно
зависимы.
линейно
зависимы.
 Как и в Т.4 предположим, что
Как и в Т.4 предположим, что
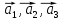 некомпланарные вектора, иначе система
будет линейно зависима. Но тогда
некомпланарные вектора, иначе система
будет линейно зависима. Но тогда
 – базис
– базис
 ,
то есть любой четвертый вектор будет
линейной комбинацией трех других, значит
вся система линейно зависима.
,
то есть любой четвертый вектор будет
линейной комбинацией трех других, значит
вся система линейно зависима.
Билет 17. Базис и размерность линейного пространства, теорема о разложении по базису.

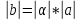







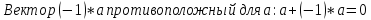












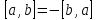
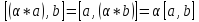


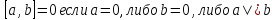
 – направляющий вектор,
то есть
– направляющий вектор,
то есть