4. Вращательное движение тела.

   1. Общие сведения и понятия.

Движение твёрдого тела, при котором какие-либо две точки тела остаются неподвижными, называется вращательным движением тела.

Пусть точки А и В тела неподвижны: . Возьмём любую точку С тела: .

Т.к. , то точка С может двигаться только по окружности радиуса ОС с центром на прямой АВ. Плоскость окружности прямой АВ.

Будем приближать точку С к прямой АВ. Радиус окружности будет уменьшаться и, когда точка С попадёт на прямую АВ, обратится в 0, т.е. точка С остановится. Следовательно, вся прямая АВ состоит из неподвижных точек тела.

Если в твёрдом теле есть две неподвижные точки, то в нём существует целое множество неподвижных точек, образующих прямую, проходящую через две неподвижных точки. Эта прямая называется осью вращения тела.

В силу указанного свойства вращательного движения положение всех точек тела можно найти, если будет указан угол поворота тела вокруг оси вращения. Этот угол вводится следующим образом.

С началом в произвольной точке оси вращения выбираем неподвижную систему координат Oxyz: оси Ox и Oy оси, а ось Oz – вдоль оси вращения. С началом в этой же точке строим подвижную систему 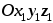: оси оси вращения, а

ось – вдоль оси (совпадает с осью Oz). Эти оси прикреплены к точкам тела и движутся вместе с телом. При вращении тела подвижные оси поворачиваются относительно неподвижных Ox и Oy, образуя с ними угол . Это и есть угол поворота тела.

Зная этот угол, можно определить положение всех точек тела в пространстве.

Если задать этот угол как функцию от времени t, то получим закон (или уравнение) вращательного движения тела:

2222\* MERGEFORMAT ()

Угол поворота тела должен измеряться в радианах: .

2. Угловая скорость и угловое ускорение тела.

Если задан закон (22), то можно найти

Эти величины (омега) и (эпсилон) называются, соответственно, угловой скоростью и угловым ускорением тела при вращательном движении. Таким образом:

2323\* MERGEFORMAT ()

2424\* MERGEFORMAT ()

Равенства (23) и (24) определяют величины угловой скорости и углового ускорения. Для того, чтобы можно было определить не только скорость изменения угла и угловой скорости, но и направление, в котором это изменение происходит (угол возрастает, или уменьшается; угловая скорость возрастет, или уменьшается) вводятся векторы угловой скорости и углового ускорения тела.

Вектор угловой скорости тела направляют вдоль оси вращения от произвольной точки оси в ту сторону, с которой вращение тела выглядит происходящим против хода часовой стрелки.

Вектор углового ускорения тела также направлен вдоль оси вращения: в одну сторону с вектором угловой скорости, если модуль угловой скорости возрастает; в противоположную сторону – если модуль угловой скорости уменьшается.

При практических расчётах положительное направление угла поворота задаётся:

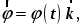2525\* MERGEFORMAT ()

где – орт оси вращения z (как правило – в ту сторону, откуда вращение видно происходящим против часовой стрелки). Тогда формулы (23), (24) определяют проекции угловой скорости и углового ускорения тела на ось вращения:

2626\* MERGEFORMAT ()

2727\* MERGEFORMAT ()

Если , то вектор направляют в положительную сторону оси вращения (так же, как и ), а если , то – в отрицательную сторону оси вращения (противоположно к ).

Если , то векторы и направлены одинаково; если же , то – противоположно!

3. Определение скорости и ускорения произвольной точки вращающегося тела.

Пусть задано уравнение (22) вращательного движения тела и теле выбрана произвольная точка М. Требуется найти её векторы скорости и ускорения в любой момент времени.

Т.к. закон вращения известен, то по формулам (26) и (27) можно найти векторы угловой скорости и углового ускорения тела. Положение точки в теле зададим её расстоянием от оси вращения R (радиус окружности, по которой движется точка).

Изобразим вид тела сверху (с положительного направления оси вращения) и перейдём к естественному способу задания движения точки тела: . Тогда

Таким образом, окончательно получаем.

Проекция скорости точки вращающегося тела на касательную к окружности

2828\* MERGEFORMAT ()

модуль скорости точки тела

2929\* MERGEFORMAT ()

касательное ускорение точки вращающегося тела

3030\* MERGEFORMAT ()

нормальное ускорение точки тела

3131\* MERGEFORMAT ()

модуль ускорения точки тела

3232\* MERGEFORMAT ()

Получим векторные формулы для скорости и ускорения точки вращающегося тела.

Рассмотрим векторное произведение

Его модуль равен

что полностью совпадает с выражением для модуля скорости точки. Как легко видеть, совпадают и направления. Поэтому

3333\* MERGEFORMAT ()

Равенство (33) называется формулой Эйлера для вектора скорости точки вращающегося тела.

Из выражения (33) получаем

Далее

Поэтому

3434\* MERGEFORMAT ()

или

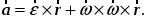3535\* MERGEFORMAT ()

Сравнивая с ранее полученной формулой для ускорения точки, получаем

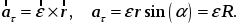3636\* MERGEFORMAT ()

3737\* MERGEFORMAT ()

Согласно равенствам (29), (30) и (31) модули скорости, касательного и нормального ускорений точек тела в данный момент времени пропорциональны их расстояниям до оси вращения. Поэтому при удалении от оси вращения все указанные величины линейно возрастают.