
тер мех решения
.docxЗАДАНИЕ С1–30

Дано: P= 25 кН, М= 100 кН∙м, F1= 10 кН, F4= 40 кН, а= 0,5 м
Найти: Реакции связей в т. А и В
РЕШЕНИЕ:
Рассмотрим равновесие жесткой рамы. На
раму действуют: силы
 и
и
 ,
пара сил с моментом М, натяжение
троса
,
пара сил с моментом М, натяжение
троса
 (
( )
и реакции связей
)
и реакции связей
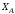 ,
,
 ,
,
 .
.
Неизвестны реакции связей
 ,
,
 ,
,
 .
.
Для полученной плоской системы сил составим три уравнения равновесия:
 ,
,
 (1)
(1)
 ,
,
 (2)
(2)
 ,
,
 (3)
(3)
Из уравнения (3):

 84,98 (кН)
84,98 (кН)
Из уравнения (2):
 -68,95 (кН)
-68,95 (кН)
Из уравнения (1):
 13,83 (кН)
13,83 (кН)
Реакции, полученные со знаком «минус», в действительности имеют направление противоположное принятому на рисунке.
Проверка:



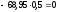

Ответ: ХА = 13,83 кН, YA = -68,95 кH, RB = 84,98 кH
ЗАДАНИЕ С3–30
Дано: Р=5 кН, М=6 кНм, l=0,8 м, F3=8 кН, F1=4 кН.
Найти: реакции связей А, В и стержня.
РЕШЕНИЕ:
Рассмотрим равновесие плиты. На нее действуют сила тяжести Р, силы F1, F3, пара сил с моментом М и реакции связей А(ХА, YА, ZА), В(ХВ, ZВ) и стержня N (считаем его растянутым).
Составляем уравнения равновесия пространственной системы сил:
 ;
;
 (1)
(1)
 ;
;
 (2)
(2)
 ;
;
 (3)
(3)
 ;
;
 (4)
(4)
 ;
;
 (5)
(5)
 ;
;
 (6)
(6)
Из (5):
 =
= =
2,9 (кН)
=
2,9 (кН)
Из
(4):
 =
= =
0
=
0
Из (6):
 =
= =
–9,3 (кН)
=
–9,3 (кН)
Из (1):
 =
= =
5,83 (кН)
=
5,83 (кН)
Из (2):
 =
= =
–8,55 (кН)
=
–8,55 (кН)
Из (3):
 =
= =
2,5 (кН)
=
2,5 (кН)
Реакции, полученные со знаком «минус», в действительности имеют направление противоположное принятому на рисунке.
|
XA |
YA |
ZA |
ХB |
ZB |
N |
|
кН |
|||||
|
5,83 |
–8,55 |
2,5 |
–9,3 |
0 |
2,9 |
ЗАДАНИЕ К1-30
к1а
Дано:
уравнения движения точки в плоскости
ху:
 ,
,
 ;
;
 1
с.
1
с.
Найти:
уравнение траектории точки; скорость
и ускорение, касательное и нормальное
ускорение и радиус кривизны траектории
в момент
 .
.
РЕШЕНИЕ:
1. Уравнение траектории. Для определения
уравнения траектории точки исключим
время
 из заданных уравнений движения.
из заданных уравнений движения.
Тогда,
 и
и
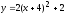 – это парабола.
– это парабола.
2. Скорость точки. Скорость найдем
по ее проекциям на координатные оси:
 ,
где
,
где
 ,
,
 .
При
.
При
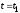 =1
с
=1
с
 (см/с),
(см/с),
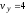 (см/с),
(см/с),
 =
4,12 (см/с).
=
4,12 (см/с).
3. Ускорение точки. Находим аналогично:
 ,
,
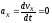 ,
,
 и при
и при
 =1
с
=1
с  (см/с2),
(см/с2),
 (см/с2),
(см/с2),
 (см/с2).
(см/с2).
4. Касательное ускорение. Найдем,
дифференцируя равенство
 .
Получим
.
Получим
 ,
откуда
,
откуда
 и при
и при
 =1
с
=1
с
 (см/с2).
(см/с2).
5. Нормальное ускорение.
 (см/с2).
(см/с2).
6.
Радиус кривизны траектории.
 (см).
(см).
|
v |
a |
a |
an |
|
|
см/с |
см/с2 |
см |
||
|
4,12 |
4 |
3,88 |
0,96 |
17,7 |
к1б
Дано:
Точка движется по дуге окружности
радиуса
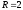 м
по закону
м
по закону
 ;
;
 1
с.
1
с.
Найти:
скорость и ускорение точки в момент
 .
.
РЕШЕНИЕ:
Скорость точки
 ,
при
,
при
 =1
с
=1
с
 =
–1,05(м/с).
=
–1,05(м/с).
Ускорение находим по касательной и
нормальной составляющим:
 (м/с2);
(м/с2);
 (м/с2);
(м/с2);
 =
1,10(м/с2).
=
1,10(м/с2).
ЗАДАНИЕ К2–30
Дано: r1=
2 см, R1= 4 см, r2= 6 см, R2=
8 см, r3= 12 см, R3= 16 см,
 ,
t1=2 c.
,
t1=2 c.
Найти: скорости
 ,
,
 ,
ускорения
,
ускорения
 ,
,
 ,
,
 .
.
РЕШЕНИЕ:
Скорости точек, лежащих на ободах колес
радиуса
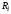 ,
обозначим через
,
обозначим через
 ,
а точек, лежащих на ободах колес радиуса
,
а точек, лежащих на ободах колес радиуса
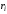 ,
через
,
через
 .
.
Угловые скорости всех колес.
 Т.к.
Т.к.
 ,
то
,
то
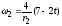 .
.
Т.к. колеса 3 и 2 связаны ременной передачей,
то
 или
или
 и
и
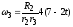 .
Колеса 1 и 3 находятся в зацеплении,
следовательно,
.
Колеса 1 и 3 находятся в зацеплении,
следовательно,
 ,
то есть
,
то есть
 и отсюда
и отсюда
 .
.
Скорости
 ,
,
 .
.
 ,
,
 .
.
При t1=2 c
 =
16 (см/с),
=
16 (см/с),
 =
21,3 (см/с).
=
21,3 (см/с).
Угловое ускорение
 .
.
 ,
следовательно
,
следовательно
 =
= =
–1,33(1/с2).
=
–1,33(1/с2).
Ускорение
 .
Для т.А
.
Для т.А
 ,
где
,
где
 ,
,
 .
Угловое ускорение
.
Угловое ускорение
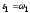 =
= =
= =
–3,56 (1/с2). Таким образом при t1=2
c
=
–3,56 (1/с2). Таким образом при t1=2
c
касательная составляющая
 (см/с2),
(см/с2),
нормальная составляющая
 =
= =
3,6 (см/с2),
=
3,6 (см/с2),
полное ускорение
 =
= =
7,9 (см/с2).
=
7,9 (см/с2).
Ускорение
 .
Т.к. груз 5 совершает поступательное
движение, то
.
Т.к. груз 5 совершает поступательное
движение, то
 .
= –7,1 (см/с2).
.
= –7,1 (см/с2).
|
vВ |
vС |
2 |
aА |
a5 |
||
|
см/с |
1/с2 |
см/с2 |
||||
|
16 |
21,3 |
–1,33 |
7,9 |
–7,1 |
||
ЗАДАНИЕ Д1-30
Дано:
 =2
кг,
=2
кг,
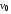 =20
м/с, Q=6 Н, R=
=20
м/с, Q=6 Н, R= Н,
Н,
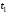 =2,5
с,
=2,5
с,
 Н,
Н,
 =0,2.
=0,2.
Найти:
 - закон движения груза на участке ВС
- закон движения груза на участке ВС
РЕШЕНИЕ:
1) Рассмотрим движение груза на участке
АВ, считая груз материальной точкой. На
груз действуют сила тяжести
 ,
реакция стенки
,
реакция стенки
 постоянная сила
постоянная сила
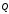 и сила сопротивления
и сила сопротивления
 .
Проведем ось
.
Проведем ось
 вдоль АВ. Составим дифференциальное
уравнение движение в проекции на эту
ось:
вдоль АВ. Составим дифференциальное
уравнение движение в проекции на эту
ось:
 или
или
 .
.

Перепишем это уравнение с учетом того,
что
 :
:
 .
Обозначим
.
Обозначим
 и
и
 .
Тогда
.
Тогда
 ,
интегрируем:
,
интегрируем:
 .
.
Постоянную С1 находим по начальным
условиям: при

 ,
что дает
,
что дает
 .
Следовательно
.
Следовательно
 .
Отсюда получаем
.
Отсюда получаем
 .
.
При перемещении
груза в точку В
 =2,5
с,
=2,5
с,
 .
Тогда
.
Тогда
 =18,03
(м/с).
=18,03
(м/с).
2).
При рассмотрении движения груза на
участке ВС найденная скорость будет
для движения на этом участке начальной
скоростью. Составим дифференциальные
уравнения движения груза в проекции на
оси
 и
и
 .
.
 и
и
 .
Тогда
.
Тогда
 и
и
 .
.
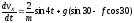 .
Обозначим
.
Обозначим
 и
и
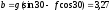 .
Разделяя переменные и интегрируя
получим
.
Разделяя переменные и интегрируя
получим
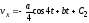 ;
при начальных условиях при
;
при начальных условиях при
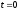
 и
и
 .
То есть
.
То есть
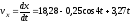 .
.
После
интегрирования:  .
Т.к. при
.
Т.к. при

 то
то
 и окончательно искомый закон движения
груза на участке ВС будет
и окончательно искомый закон движения
груза на участке ВС будет

ЗАДАНИЕ Д3–30
Дано: R=
1,2 м,
 24 кг,
24 кг,
 8 кг,
8 кг,
 10
с-1, ОС= R,
10
с-1, ОС= R,
 м,
м,
 Нм
Нм
Найти:
 – закон изменения угловой скорости
платформы
– закон изменения угловой скорости
платформы
РЕШЕНИЕ: 
Рассмотрим механическую систему,
состоящую из платформы и груза D. Для
определения
 применим теорему об изменении кинетического
момента системы относительно оси z:
применим теорему об изменении кинетического
момента системы относительно оси z:
 .
.
На систему действуют внешние силы: силы
тяжести платформы и груза
 и
и
 ,
реакции
,
реакции
 и и момент М. Т.к. силы
и и момент М. Т.к. силы
 и
и
 параллельны оси z, а реакции
параллельны оси z, а реакции
 и
и
 пересекают ее, то их моменты относительно
этой оси равны нулю. Тогда
пересекают ее, то их моменты относительно
этой оси равны нулю. Тогда
 и
и  .
После интегрирования
.
После интегрирования
 . (1)
. (1)
Для рассматриваемой механической
системы  ,
где
,
где
 и
и
 – кинетические моменты платформы и
груза соответственно.
– кинетические моменты платформы и
груза соответственно.
Платформа вращается вокруг оси z,
следовательно
 .
По теореме Гюйгенса
.
По теореме Гюйгенса
 (
( –
момент инерции относительно оси
параллельной оси z и проходящей
через центр платформы. Но
–
момент инерции относительно оси
параллельной оси z и проходящей
через центр платформы. Но
 .
Тогда
.
Тогда
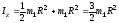 .
.
Следовательно
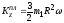 .
.
Для определения
 рассмотрим движение груза D
как сложное, считая его движение по
платформе относительным, а вращение
самой платформы – переносным движением.
Тогда
рассмотрим движение груза D
как сложное, считая его движение по
платформе относительным, а вращение
самой платформы – переносным движением.
Тогда
 .
.
Т.к.
 ,
то
,
то
 .
.
 .
Тогда, по теореме Вариньона,
.
Тогда, по теореме Вариньона,
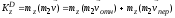 =
= =
=
=
Из рисунка:
 =
= (м),
(м),
 =
= =
= =
= =
=
=
= =
= .
.
Тогда,
 и
и
 .
После подстановки
.
После подстановки
 =
= .
.
Тогда уравнение (1) примет вид
 .
.
Постоянную
интегрирования определим по начальным
условиям: при
 ,
,
 .
Получим
.
Получим
 .
.
Следовательно, искомая зависимость будет иметь вид:

ЗАДАНИЕ Д5–30
Дано:
r=0,6R,
 ,
,
 ,
,
 ,
=30о, =60о.
,
=30о, =60о.
Найти:
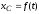 – закон движения центра масс,
– закон движения центра масс,
 – наименьший коэффициент трения, при
котором возможно качение без скольжения.
– наименьший коэффициент трения, при
котором возможно качение без скольжения.
РЕШЕНИЕ:
Барабан совершает плоскопараллельное
движение под действием сил
 ,
,
 ,
,
 ,
,
 (направление
(направление
 произвольно). Составим диф. уравнения
плоскопараллельного движения:
произвольно). Составим диф. уравнения
плоскопараллельного движения:
 ;
;
 (1)
(1)
 ;
;
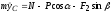 (2)
(2)
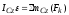 ;
;
 (3)
(3)
(положительное направление моментов в направлении вращения барабана при его движении от т.О).
1) Определение
 .
В нашей задаче
.
В нашей задаче
 и
и
 .
Учтем, что
.
Учтем, что
 и при качении без скольжения в т. В
находится мгновенный центр скоростей.
Тогда
и при качении без скольжения в т. В
находится мгновенный центр скоростей.
Тогда
 ,
,
 или
или  . (4)
. (4)
Тогда из уравнения (3)  ,
(5)
,
(5)
Сложив его почленно с (1) получим
 =
= =
=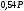 .
.
Отсюда, т.к.
 ,
,
 .
.
Интегрируем:
 и
и  .
.
По начальным условиям при
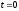
 и
и
 получаем
получаем
 .
Окончательно закон движения центра
масс принимает вид
.
Окончательно закон движения центра
масс принимает вид
 .
.
2) Определение
 .
При качении без скольжения сила трения
должна удовлетворять неравенству
.
При качении без скольжения сила трения
должна удовлетворять неравенству
 . (6)
. (6)
Из уравнения (2), учитывая, что
 ,
,
 =
= =
=
Из уравнения (5), учитывая, что

 .
Отсюда, т.к.
.
Отсюда, т.к.


Подставим значения
 и
и
 в неравенство (6)
в неравенство (6)
 ,
откуда
,
откуда
 .
Таким образом, наименьший коэффициент
трения, при котором возможно качение
барабана без скольжения
.
Таким образом, наименьший коэффициент
трения, при котором возможно качение
барабана без скольжения
 .
.
Крупнейшая в интернете база решений из сборников заданий для курсовых работ Тарга С.М. (1982, 1983, 1988, 1989 гг.) находится по адресу www.targ.stig85.ru
