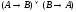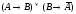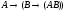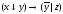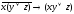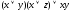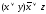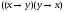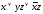Контрольная работа «Математическая логика и теория алгоритмов» База заданий
-
Логика и исчисление высказываний
-
Записать высказывания в виде формул логики высказываний.
-
Сегодня мы пойдем в кино или поедем кататься на лыжах.
-
Если будет хорошая погода, то мы пойдем гулять.
-
Если х=5 и у=3, то х>y.
-
Людоед голоден только тогда, когда он давно не ел.
-
Иванов сдал экзамен и получил 5 неравнозначно тому, что Иванов сдал экзамен и получил 5
-
Если он бегает по лужайке и у него длинные уши, то он или заяц или осел
-
-
Построить таблицы истинности для формул
-
-
Доказать, что формулы являются тавтологиями
-
-
Доказать полноту (неполноту) систем булевых функций
-
{⊕, ~}
-
{|}
-
{↓}
-
{⌐,&}
-
{⌐,}
-
{⌐,→}
-
{→,0}
-
{⊕,⋁,1}
-
{&, ⋁,→}
-
{→, ⊕}
-
{→, ~}
-
{~, ⊕}
-
-
Получить СДНФ для формул, а затем перейти к СКНФ:
-
-
Получить СКНФ, а затем перейти к СДНФ
-
-
Получить МДНФ для формул
-
-
Логика и исчисление предикатов. Автоматическое доказательство теорем
-
Записать на языке предикатов
-
все студенты учатся;
-
некоторые студенты отличники;
-
Детям до 16 лет и роботам входить запрещено;
-
всем детям до 16 лет и роботам надлежит получить справки;
-
для любого числа можно найти большее число;
-
x+y=z;
-
каждый студент выполнил, по крайней мере, одну лабораторную работу.
-
всякий предмет обладает свойством А;
-
нечто обладает свойством В;
-
если студент отлично учится, не имеет нарушений и занимается общественной работой, то он получает повышенную стипендию;
-
не всегда из того, что x лучше y, а y лучше z следует, что x лучше z;
-
каждое рациональное число есть действительное число;
-
некоторые действительные числа являются рациональными;
-
«Все счастливые семьи похожи друг на друга, каждая несчастливая семья несчастлива по-своему»
-
всякое N, делящееся на 12 делится на 2, 4 и 6.
-
-
Получить множество дизъюнктов.
-
xy, z, v(R(x, y, z, v)&L(y, z))
-
x, y, z (P(x)&Q(x, y)R(z))
-
x, y, z (P(x)Q(x, y)R(z)M(y))
-
x P(x)&x Q(x) x(R(x)P(x))
-
x(y P(x, y)z(Q(x, z)R(z)))
-
(x P(x) y Q(y))&(x, y R(x, y)y L(y))
-
x P(x) y R(y)
-
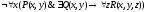
-

-

-
-
Преобразовать теоремы в вопросы и получить ответы с помощью метода резолюции.
-
А1: Все, что обладает свойством P, имеет свойство R.
-
А2: Все, что обладает свойством R, имеет свойство Q.
Вопрос: Существует ли нечто, что не обладает свойством P или обладает свойством Q?
-
А1: Если х есть часть у и у есть часть z, то х есть часть z.
А2: Палец есть часть руки.
А3: Кисть есть часть руки.
Вопрос: Частью кого является рука?
-
А1: Кто ходит в гости по утрам, тот поступает мудро.
А2: Если у кого угодно есть воздушный шарик, тот ходит в гости по утрам.
А3: У Пяточка есть воздушный шарик.
Вопрос: Кто поступает мудро?
-
А1: Если робот обработал деталь, то ее забирает штабелер.
А2: Если деталь поступила на обработку, то ее обработает робот.
А3: Если человеку нужна деталь, то она поступит на обработку.
А4: Человеку нужна втулка.
Вопрос: Что заберет штабелер?
-
A1: Некоторые пациенты любят своих докторов.
А2: Ни один пациент не любит знахаря.
Теорема: Никакой доктор не является знахарем.
-
Для заданной системы аксиом доказать теорему.
-
А1:
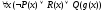
-
А2:
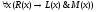
А2:

А4:

Т:

-
А1:

Т:

-
А1:
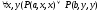
Т:

Т:

-
А1:
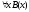
А2:

А3:

А4:

Т: