Контрольная работа на тему: «Задачи целочисленного программирования»

Задача.Задачу решить методом ветвей и границ. Корневую задачу решить симплекс-методом, остальные – графически. Построить дерево решений.

Вариант № 4.

L= 6x₁+ 9x₂→max5x₁+ 7x₂≤ 35 4x₁+ 9x₂≤ 36x₁,x₂≥ 0, цел

Решение:

Решим задачу симплекс-методом. Для этого приведём исходные данные к каноническому виду.

Составим симплекс-таблицу.

L	x1	x2	x3	x4	Решение	Базис	Остаток
0	5	7	1	0	35	x3	35/7 = 5
0	4	9	0	1	36	x4	36/9 = 4
1	-6	-9	0	0	0	L

Вводим x₂в базис вместоx₄.

L	x1	x2	x3	x4	Решение
0	5	7	1	0	35
0	4/9	1	0	1/9	4
1	-6	-9	0	0	0

L	x1	x2	x3	x4	Решение	Базис	Остаток
0	17/9	0	1	-7/9	7	x3	7 : 17/9 = 63/17
0	4/9	1	0	1/9	4	x2	4 : 4/9 = 9
1	-2	0	0	1	36	L

Вводим x₁в базис вместоx₃.

L	x1	x2	x3	x4	Решение
0	1	0	9/17	-7/17	63/17
0	4/9	1	0	1/9	4
1	-2	0	0	1	36

L	x1	x2	x3	x4	Решение	Базис
0	1	0	9/17	-7/17	63/17	x1
0	0	1	-4/17	5/17	40/17	x2
1	0	0	18/17	3/17	738/17	L

x₁ = 63/17, x₂ = 40/17, L = 738/17

Обозначим данную задачу как ЛП0

Так как решение не удовлетворяет условиям целых чисел x₁иx₂, то изменим пространство решений задачи. Разделим задачу ЛП0 на ЛП1 с условиемx₁≤ 3 и ЛП2 с условиемx₁≥ 4.

Наиболее оптимальное решение ЛП1: x₁= 3,x₂= 2,L= 42.

Наиболее оптимальное решение ЛП2: x₁= 4,x₂= 2,L= 43.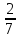

Из данных двух задач наиболее оптимальным является ЛП2. Но ЛП2 не удовлетворяет условиям задачи, т.к. x₂не целое число. Разделим ЛП2 на ЛП3 и ЛП4 с условиямиx₂≤ 2 иx₂≥ 3 соответственно.

Для ЛП4 решений нет. Наиболее оптимальное решение ЛП3: x₁= 4,x₂= 2,L= 43.

Задача ЛП3 не удовлетворяет условию целых чисел x₁. Разделим ЛП3 на две задачи ЛП5 с условиемx₁≤ 4 и ЛП6 с условиемx₁≥ 5.

Оптимальное решение ЛП5: x₁= 4,x₂= 2,L= 42.

Оптимальное решение ЛП6: x₁= 5,x₂= 1,L= 42.

Задача ЛП5 удовлетворяет всем условиям корневой задачи, но у ЛП6 наиболее оптимальное решение. Так как ЛП6 не удовлетворяет целочисленным значениям переменных, разделим её на задачи ЛП7 и ЛП8 с условиями x₂≤ 1 иx₂≥ 2 соответственно.

У задачи ЛП7 решений нет. Оптимальное решение ЛП8: x₁= 5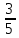,x₂= 1,L= 42. Решение ЛП8 не удовлетворяет условию целочисленных значений переменных, но она наиболее оптимальное решение, чем ЛП5. Поэтому продолжим искать решение задачи. Разделим ЛП8 на две задачи ЛП9 и ЛП10 с условиямиx₁≤ 5 иx₁≥ 6 соответственно.

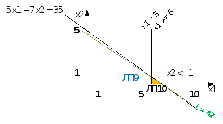
Оптимальное решение ЛП9: x₁= 5,x₂= 1,L= 39.

Оптимальное решение ЛП10: x₁= 7,x₂= 0,L= 42.

Отсюда следует, что задачи ЛП5 и ЛП10 оба удовлетворяют всем условиям корневой задачи и оба являются оптимальными решениями.