
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Пермский национальный исследовательский политехнический университет»
Кафедра ИТАС ЭТФ
Контрольные работы
|
по дисциплине «Исследование операций и МОС» |
|
|
Выполнил студент гр. |
РИС-13бзу | |
|
Габитов М.Т. | |||
|
(Фамилия И.О.) | |||
|
13-ЭТФз-396 | |||
|
(номер зачетной книжки) | |||
|
| |||
|
(дата, подпись) | |||
|
Проверил |
профессор | ||
|
|
(должность) | ||
|
Гольдштейн А.Л. | |||
|
(Фамилия И.О.) | |||
|
| |||
|
(оценка) | |||
|
| |||
|
(дата, подпись) | |||
Пермь 2015 г.
Контрольная работа на тему: «Игровые задачи».
Задача.Найти решение игры двух лиц с нулевой суммой графическим методом. Для сокращения числа стратегий использовать отношение доминирования. В приведенных ниже вариантах платежных матриц строки соответствуют стратегиям 1-го игрока, а столбцы – стратегиям 2-го игрока. Платежи имеют смысл Выигрыша (В) или проигрыша (П) для 1-го игрока, как указано ниже в скобках.
Вариант № 4.
|
(В) |
|
|
|
|
1 |
3 |
0 |
4 |
|
-5 |
1 |
-6 |
2 |
|
3 |
-2 |
3 |
-1 |
|
5 |
3 |
4 |
3 |
|
2 |
5 |
2 |
6 |
Решение:
Принцип гарантированного результата будут применять оба игрока: каждый оценивает свои стратегии по наихудшему результату, показанному в добавленных строке и столбце.
|
|
B1 |
B2 |
B3 |
B4 |
min |
|
A1 |
1 |
3 |
0 |
4 |
0 |
|
A2 |
-5 |
1 |
-6 |
2 |
-6 |
|
A3 |
3 |
-2 |
3 |
-1 |
-2 |
|
A4 |
5 |
3 |
4 |
3 |
3 |
|
A5 |
2 |
5 |
2 |
6 |
2 |
|
max |
5 |
5 |
4 |
6 |
|
Из этих оценок определяем:
maxi minj(платежей) =vн= 3 – нижняя цена игры,
minjmaxi(платежей) =vв= 4 – верхняя цена игры.
Верхняя и нижняя границы не равны => решение находится в области смешанных стратегий => седловой точки нет => игроки будут применять более одной стратегии.
Для решения графическим способом нужно стратегии одного из игроков уменьшить до двух. Уберем стратегии, которые ведут к худшему результату для игрока А. В результате сравнения А1 и А2 видим, что стратегия А2 менее эффективна на всех стратегиях игрока В.
При сравнении А1 и А5 стратегия А1 менее эффективна. При сравнении А3 и А4 стратегия А3 менее эффективна.
В результате получим следующую матрицу:
|
|
B1 |
B2 |
B3 |
B4 |
|
A4 |
5 |
3 |
4 |
3 |
|
A5 |
2 |
5 |
2 |
6 |
Построим графическое решение для игрока А:
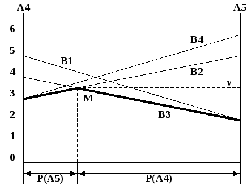
Гарантированные выигрыши игрока А лежат на нижней грани, выделенной жирной линией. Найдём координаты точки М:
уравнение прямой, характеризующей выигрыши игрока А при фиксированной стратегии В2: y= 2x+ 3;
уравнение прямой, соответствующей В3: y= -2x+ 4;
находим пересечение этих прямых: 2x+ 3 = -2x+ 4;
отсюда x= 0,25 – это вероятность применения стратегии А5, (1-x) = 0,75 – вероятность применения стратегии А4;y= 2 * 0,25 + 3 = 3,5 – это цена игры –v.
Найдём решение для игрока В:
При сравнении стратегии В1 и В3 стратегия В1 худшая. При сравнении стратегии В2 и В4 стратегия В4 худшая.
|
|
B2 |
B3 |
|
A4 |
3 |
4 |
|
A5 |
5 |
2 |

Найдём координаты точки М:
уравнение прямой стратегии А4: y=x+ 3;
уравнение прямой стратегии А5: y= -3x+ 5;
находим пересечение прямых: x+ 3 = -3x+ 5,
следовательно, x = 0,5 – вероятность В3, (1-x) = 0,5 – вероятность В2;
y= 0,5 + 3 = 3,5 – цена игрыv.
Ответ:оптимальное решение игрока А состоит в применении стратегии А4 с вероятностью 0,75 и стратегии А5 с вероятностью 0,25. Средняя цена выигрыша = 3,5. Оптимальное решение игрока В состоит в применении стратегий В2 и В3 с вероятностью 0,5 каждый. Средняя цена проигрыша 3,5.
