Formuly_sokrashchennogo_umnozhenija_shpargalka

Формулы сокращенного умножения

Разность квадратов: ;

Квадрат суммы: ;

Квадрат разности: ;

Сумма кубов: ;

Разность кубов: ;

Куб суммы: ;

Куб разности: ;

Квадрат трехчлена: .

Замечание: Формулы в прямом прочтении дают сокращенное умножение многочленов или возведение их в степень. В обратном прочтении – разложение многочлена на множители.

Формула разложения квадратного трехчлена на множители

Следует помнить, что квадратный многочлен можно разложить на множители, если у него есть действительные корни, т. е. . При этом надо обратить особое внимание, что если , то формула будет иметь вид:

,

и Вы скорее всего не заметили формулу полного квадрата двучлена (квадрат суммы или квадрат разности).

Стоит так же помнить, что если , то квадратный трехчлен на множители не раскладывается. Так, например, не стоит пытаться разложить на множители неполный квадрат суммы или разности (второй множитель формул суммы и разности кубов): .

Формулы корней квадратного уравнения

Общий вид квадратного уравнения: .

Дискриминант квадратного уравнения: .

Если , то квадратное уравнение действительных корней не имеет.

Если , то квадратное уравнение имеет одни действительный корень кратности два, который находится по формуле: .

Если , то квадратное уравнение имеет два действительных корня, которые находятся по формулам: .

Формулы корней квадратного уравнения с четным вторым коэффициентом.

Общий вид уравнения: .

Дискриминант: .

Условия существования корней прежние, т. е. .

Корни: .

Теорема Виета.

Квадратное уравнение называется приведенным, если его старший коэффициент равен 1. Любое квадратное уравнение можно привести, разделив обе его части на старший коэффициент.

Общий вид приведенного квадратного уравнения: .

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение равно свободному члену.

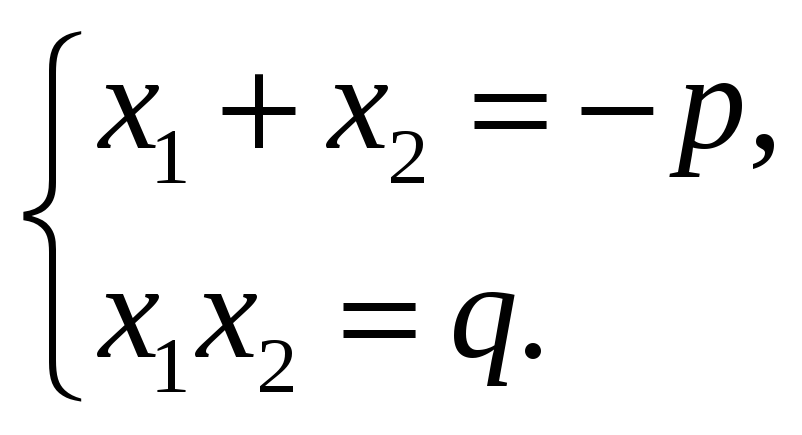
Верна и обратная теорема.