3.2. Изменение моментов инерции при параллельном переносе осей

Если оси х, у параллельны центральным осям х_с, у_с (рис. 3.2), то справедливы следующие соотношения:

;

;

. (3.7)

Здесь a и b – координаты точки 0 (с учетом знаков), т.е. нового начала координат в старой системе координат х_c, у_c.

Первые слагаемые в правых частях равенств (3.7) являются собственными моментами инерции фигуры, а вторые слагаемые переносными моментами инерции. Моменты инерции относительно осей, параллельных центральным, всегда увеличиваются по отношению к центральным на величину, равную произведению площади сечения на квадрат расстояния между рассматриваемыми осями.

Для сложных сечений моменты инерции связаны следующими соотношениями:

; ;. (3.8)

3.3. Изменение моментов инерции при повороте осей координат

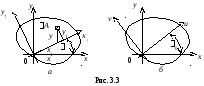
При повороте осей (х₁; у₁) на какой-либо угол  по отношению к исходным (рис. 3.3, а) моменты инерции изменяются:

,

,

. (3.9)

Эти зависимости справедливы только для осей с общим началом координат. Положительный угол  отсчитывается от оси х в направлении кратчайшего поворота ее до совмещения с осью у.

Определение положения главных осей и главных моментов инерции

Положение главных осей находится по формуле

, (3.10)

где ₀ – угол, на который нужно повернуть оси х и у, чтобы получить положение главных осей. При ₀ > 0 поворот оси х до совмещения с главной осью производится против часовой стрелки (рис. 3.3, б).

Главные моменты инерции вычисляются по формуле (3.9), если в них положить  = ₀, или по формулам:

Рис. 3.4

Р

ис. 3.4. Окончание

,

. (3.11)

В формулах (3.11) верхние знаки следует брать при , а нижние – при.

Правило инварианта: . При повороте осей сумма осевых моментов инерции относительно перпендикулярных осей остается величиной постоянной.

3.4. Понятие о радиусе инерции

Момент инерции фигуры относительно какой-либо оси можно записать в виде произведения площади фигуры и квадрата некоторой величины, которую называют радиусом инерции:

, (3.12)

где i_x – радиус инерции относительно оси х.

Тогда

, . (3.13)

Относительно главных осей будут равны соответственно

, . (3.14)

3.5. Методика определения положения главных осей и вычисления главных моментов инерции, радиусов инерции

1. Любая сложная фигура разбивается на простейшие (прямоугольник, квадрат, треугольник, полуокружность, четверть окружности и т.д.), геометрические характеристики которых известны (рис. 3.4).

2. Проводится произвольная система прямоугольных координат (вспомогательные оси), относительно которых положение центров тяжести любой простейшей фигуры является величиной известной.

3. По формулам (3.3) определяется центр тяжести всей фигуры и проводятся центральные оси х_с и у_с, которые параллельны центральным осям простейших фигур.

4. Используя зависимость изменения моментов инерции при параллельном переносе осей (формулы (3.7), (3.8)), определяют моменты инерции и центробежный момент инерции всей фигуры относительно центральных осей.

5. По формуле (3.10) вычисляют положение главных осей инерции (угол ₀).

6. Определяют по формулам (3.11) главные моменты инерции.

7. По формулам (3.14) вычисляют главные радиусы инерции.