Пример 3

Подобрать из условия прочности поперечные сечения стальных стержней кронштейна, нагруженного силой F = 200 кН, и определить горизонтальное, вертикальное и полное перемещение узла С (рис. 2.6).

Стержень АС двутаврового поперечного сечения, стержень ВС круглого поперечного сечения. Допускаемое напряжение для материала стержней [] = 160 МПа, модуль упругости Е = 210⁵ МПа.

Решение

1. Составим уравнения равновесия и определим усилия в стержнях. Для этого мысленно вырежем узелС. В местах разрезов приложим неизвестные пока усилия в направлении, вызывающем растяжение стержней (рис. 2.7).

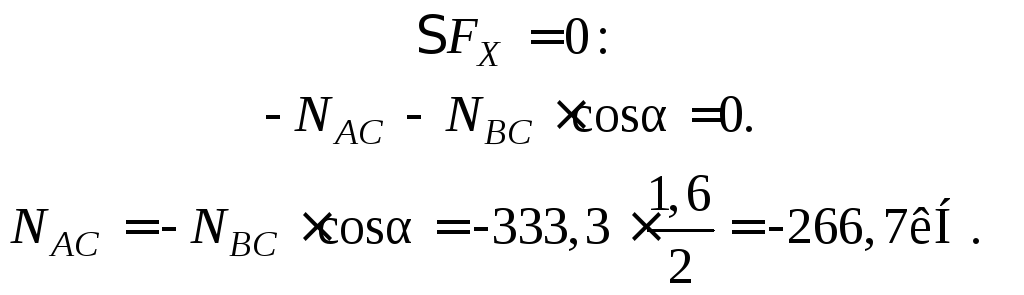
Отрицательное значение усилия N_АС указывает на то, что стержень испытывает сжатие.

2. Подбираем из условия прочности размеры стержней.

а) для стержня ВС , причем. Тогда.

Принимаем в соответствии с таблицей нормальных размеров d = 52 мм. Уточненная площадь стержня ВС см²;

б) для стержня АС А_AС см².

В соответствии с сортаментом на двутавровые балки по ГОСТ 8239–72 принимаем двутавр № 14 с F = 17,4 см².

3. Находим изменение длины каждого стержня.

а) удлинение стержня ВС

б) укорочение стержня АС

ммм

4. Определяем перемещение узловой точки С.

План перемещения представлен на рис. 2.8.

Для определения перемещения узлаС положим, что стержни в узле С не соединены между собой. Тогда стержень ВС удлинится на величину l_ВС, и стержень АС укоротится на величину l_АС. Новое положение узла С (точка С₁) определится как точка пересечения перпендикуляров к стержням ВС и АС, проведенных из конца стержней ВС + l_ВС и АС  l_АС(вместо дуг радиусов ВС + l_ВС и АС  l_АС). Из схемы видно, что горизонтальное перемещение точки С равно _Г = |l_АС| =  = 1,2 мм. Для нахождения второй координаты точки С₁  _В проведем из точки D перпендикуляр на продолжение стержня ВС. Тогда удлинение l_ВС можно представить как разность отрезков или, откуда

.

Полное перемещение узла С определяется как геометрическая сумма мм.

Контрольная работа № 1. Расчеты на прочность статически определимых систем растяжения-сжатия

Задача 1. Проверить прочность и определить перемещение свободного конца стержня. Материал стержня – сталь ([] = 160 МПа, Е = 210⁵ МПа). Расчетная схема и числовые данные выбираются в соответствии с шифром по рис. 2.9 и табл. 2.1.

Таблица 2.1

Номер строки	Цифра шифра
	1	2	3	4	5	6
	схема	а, м	F1, кН	F2, кН	F3, кН	A1, см2
1	1	0,30	15	60	100	10
2	2	0,35	20	70	110	11
3	3	0,40	45	80	122	12
4	4	0,45	50	75	130	14
5	5	0,50	35	90	125	12,5
6	6	0,55	30	65	120	15
7	7	0,60	40	75	115	20
8	8	0,65	25	50	110	16
9	9	0,70	30	85	90	14
0	10	0,75	55	77	140	13

Примечание: А₂ = 1,6А₁.