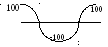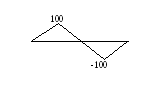лаб.чис.мед
.docЗадание
Получить распределение температуры в стержне единичной длины.
Определяющие соотношения приведены ниже. Использовать консервативную разностную схему для двух вариантов граничных условий, приведенных в таблице. Использовать для решения систем линейных алгебраических уравнений прямой метод прогонки и итерационный - метод Гаусса-Зейделя. Сравнить результаты расчета по явной и неявной схемам, для последней провести сравнение двух методов решения систем уравнений. Представить результаты (поля температур) в пяти различных моментах времени.
![]()
![]()
|
№ п/п |
НУ |
ГУ 1 T1;T2
|
ГУ 2 q
Вт/ |
|
1 |
|
0;100 |
q=0;100 |
|
2 |
|
0;150 |
q=0;150 |
|
3 |
100
100 |
0;250 |
q=0;250 |
|
4 |
|
20;100 |
q=0;100 |
|
5 |
|
20;150 |
q=0;150 |
|
6 |
100
|
20;250 |
q=0;250 |
|
7 |
|
50;150 |
q=0;150 |
|
8 |
|
50;250 |
q=0;250 |
|
9 |
|
30;150 |
q=0;150 |
|
10 |
|
30;200 |
q=0;200 |
|
11 |
|
30;250 |
q=0;250 |
|
12 |
|
10;100 |
q=0;100 |
|
13 |
|
10;150 |
q=0;150 |
|
14 |
|
10;200 |
q=0;200 |
|
15 |
|
10;250 |
q=0;250 |
|
16 |
|
40;100 |
q=0;100 |
|
17 |
|
40;150 |
q=0;150 |
|
18 |
|
40;200 |
q=0;200 |
|
19 |
|
40;250 |
q=0;250 |
|
20 |
|
0;250 |
q=0;250 |
Задание
Получить распределение температуры в стержне единичной длины.
Определяющие соотношения приведены ниже. Использовать явную и неявную разностные схемы для двух вариантов граничных условий, приведенных в таблице. Использовать для решения систем линейных алгебраических уравнений прямой метод прогонки и итерационный - метод Гаусса-Зейделя. Сравнить результаты расчета по явной и неявной схемам, для последней провести сравнение двух методов решения систем уравнений. Представить результаты (поля температур) в пяти различных моментах времени.
![]()
![]()
Задание
Получить распределение температуры в стержне единичной длины.
Определяющие соотношения приведены ниже. Использовать явную и неявную разностные схемы для двух вариантов граничных условий, приведенных в таблице. Использовать для решения систем линейных алгебраических уравнений прямой метод прогонки и итерационный - метод Гаусса-Зейделя. Сравнить результаты расчета по явной и неявной схемам, для последней провести сравнение двух методов решения систем уравнений. Представить результаты (поля температур) в пяти различных моментах времени.
![]()
![]()