
- •Федеральное государственное бюджетное образовательное учреждение
- •Тема 1. Предмет, метод и задачи статистики
- •Тема 2. Статистическое измерение и наблюдение
- •Тема 3. Сводка и группировка материалов статистического наблюдения
- •Тема 4. Абсолютные и относительные величины
- •Тема 5. Средние величины
- •Структурные средние
- •Определение моды по дискретному ряду распределения
- •Определение моды и медианы по интервальным вариационным рядам
- •Тема 6. Показатели вариации
- •Относительные показатели вариации
- •Дисперсия альтернативного признака
- •Виды дисперсий
- •Тема 7. Статистическое изучение динамики социально-экономических явлений
- •Аналитические показатели ряда динамики
- •Средние показатели в рядах динамики
- •Методы анализа основной тенденции (тренда) в рядах динамики
- •Выравнивание по уравнению прямой
- •Методы выявления сезонной компоненты
- •Основы прогнозирования
- •Тема 8. Экономические индексы
- •Тема 9. Выборочное наблюдение
- •Тема 10. Статистическое изучение взаимосвязи социально-экономических явлений
- •Парная регрессия на основе метода наименьших квадратов
- •Параметрические методы изучения связи
- •Принятие решений на основе уравнений регрессии
- •Методы изучения связи качественных признаков
- •Ранговые коэффициенты связи
- •Рекомендуемая литература
Тема 9. Выборочное наблюдение
Под выборочным наблюдением понимается такое несплошное наблюдение, при котором статистическому наблюдению подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу — по обследуемой части дать характеристику всей (генеральной) совокупности единиц. Совокупность отобранных для обследования единиц называют выборочной, а совокупность единиц, из которых производится отбор, — генеральной.
Отбор единиц в выборочную совокупность может быть повторным или бесповторным.
При повторном отборе попавшая в выборку единица подвергается обследованию, т. е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения.
При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.
Выборочное наблюдение всегда связано с определенными ошибками получаемых характеристик. Эти ошибки называются ошибками репрезентативности (представительности).
Ошибки репрезентативностиобусловлены тем обстоятельством, что выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Получаемые расхождения или ошибки репрезентативности позволяют заключить, в какой степени попавшие в выборку единицы могут представлять всю генеральную совокупность. При этом следует различать систематические и случайные ошибки репрезентативности.
Систематические ошибкирепрезентативности обусловлены нарушением принципа случайности отбора (тенденциозный отбор) и являются однонаправленными ошибками. Их можно устранить правильной процедурой отбора единиц в выборку.
Случайные ошибкирепрезентативности обусловлены действием случайных факторов, не содержащих каких-либо элементов системности. Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка ошибок выборочного наблюдения основана на теоремах теории вероятностей.
Выборка характеризуется следующими показателями:
средняя ошибка выборки(повторный отбор):
![]()
средняя ошибка выборки(бесповторный отбор):
![]()
предельная ошибка выборки— ошибка, исчисленная с заданной степенью вероятности:
![]()
где 2— выборочная дисперсия (значения признака или доли),
n— объем выборочной совокупности;
N— объем (число единиц) генеральной совокупности;
![]() – выборочная
дисперсия значения признака (х);
– выборочная
дисперсия значения признака (х);
![]() –выборочная
дисперсия доли;
–выборочная
дисперсия доли;
ω— выборочная доля (![]() ),
т.е. доля единиц, обладающих определенным
вариантом или вариантами изучаемого
признака, в выборочной совокупности ;
),
т.е. доля единиц, обладающих определенным
вариантом или вариантами изучаемого
признака, в выборочной совокупности ;
![]() —выборочная
средняя;
—выборочная
средняя;
t— коэффициент доверия (табличное значение).
Предельная ошибка выборки дает возможность выяснить, в каких пределах находится величина генеральной средней с учетом заданной вероятности;
На величину вероятности указывает множитель t. Обычно используются нормированные (табличные) значенияt, для определенных значений вероятности Ф(t):
|
t=1 |
Ф(t)= 0,683 |
|
t=2 |
Ф(t)= 0,954 |
|
t=3 |
Ф(t)= 0,997 |
Зная выборочную
среднюю величину признака (![]() )
и предельную ошибку выборки (x),
можно определить границы (пределы), в
которых заключена генеральная средняя
(
)
и предельную ошибку выборки (x),
можно определить границы (пределы), в
которых заключена генеральная средняя
(![]() ):
):
![]() или
или
![]()
Зная выборочную
долю признака (![]() )
и предельную ошибку выборки (
)
и предельную ошибку выборки (![]() ),
можно определить границы, в которых
заключена генеральная доля (р):
),
можно определить границы, в которых
заключена генеральная доля (р):
![]()
Для типической
выборки при расчете средней ошибки ()
используют не общую дисперсию, а среднюю
из внутригрупповых дисперсий (![]() ),
при серийной выборке — межгрупповую
дисперсию (2).
),
при серийной выборке — межгрупповую
дисперсию (2).
Для определения необходимой численности выборки исследователь должен задать уровень точности (предельную ошибку) выборочной совокупности с определенной вероятностью.
Численность случайной повторной выборкиопределяется по формуле:
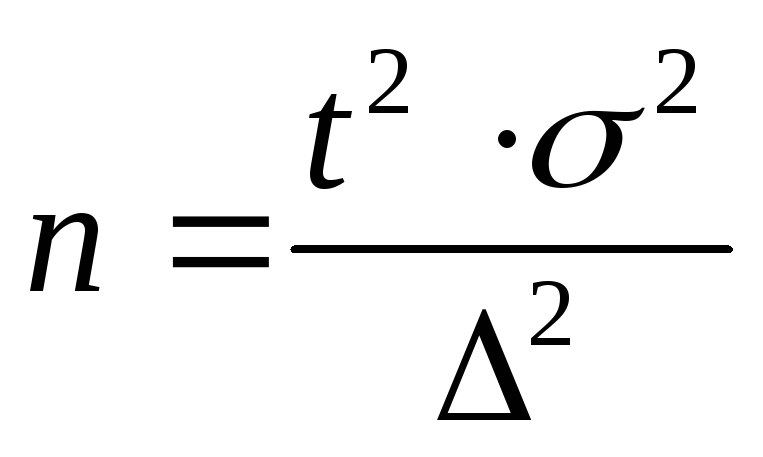 ,
или
,
или

бесповторной:
 .
.
где ![]() или
или![]() — относительная
ошибка выборки
— относительная
ошибка выборки
![]() —коэффициент
вариации
—коэффициент
вариации
Если расчет
проводится по качественному альтернативному
признаку и не известна его доля в
генеральной совокупности, её принимают
равной 0,5, так как дисперсия доли достигает
максимума:
![]() = 0,25 приω= 0,5.
= 0,25 приω= 0,5.
![]()
Пример 9.1.Для определения качества партии товара 5% от всего количества изделий были подвергнуты выборочному обследованию. Из 1000 проверенных изделий 150 были нестандартными. Определить с вероятностью 0,954 долю нестандартных изделий во всей партии.
Решение: По условию задачи дано:
|
|
Определим долю нестандартных изделий в выборочной совокупности: |
|
n = 1000 изд. |
ω
=
|
|
m = 150 изд. | |
|
t = 2 |
Из 1000 проверенных изделий |
|
w – ? Δw – ? |
15% – нестандартные изделия. |
Определим предельную ошибку выборочного наблюдения:
Δω
= t
![]()
или Δω
= 2
![]() = 0,022 или 2,2%.
= 0,022 или 2,2%.
Доверительные интервалы для доли будут равны:
p
= w![]() Δw
Δw
p
= 15%
![]() 2,2%, тогда 15% – 2,2%
2,2%, тогда 15% – 2,2%
![]() p
p![]() 15% + 2,2%.
15% + 2,2%.
Доля нестандартных изделий во всей партии будет находиться в пределах от 12,8 до 17,2% при вероятности 0,954.
Пример 9.2.Для определения среднего срока пользования краткосрочным кредитом в банке была произведена 10%-ная механическая выборка, в которую попало 200 счетов. В результате обследования установлено, что средний срок пользования краткосрочным кредитом – 30 дней при среднем квадратическом отклонении 9 дней. С вероятностью 0,997 определить пределы, в которых будет находиться средний срок пользования краткосрочным кредитом в генеральной совокупности.
Решение. Средний срок пользования кредитом в банке находится в пределах:
![]() –Δх
–Δх
![]()
![]()
![]()
![]() +
Δх .
+
Δх .
Так как выборка механическая, то ошибка выборочного наблюдения определяется по формуле:
Δх
= t
![]() ;
;
Δх
= 3
![]() =
1,81
=
1,81![]() 2
дня
2
дня
![]() =30
дн.
=30
дн.![]() 2
дн. или 30 дн.–2 дн.
2
дн. или 30 дн.–2 дн.![]()
![]()
![]() 30
дн.+2 дн.
30
дн.+2 дн.
С вероятностью 0,997 можно утверждать, что средний срок пользования краткосрочным кредитом в банке находится в пределах от 28 дней до 32 дней.
