
Тема 4. Интегральное исчисление функции одной переменной
Программный объем темы:
Первообразная, неопределенный интеграл и его основные свойства. Таблица простейших интегралов.
Непосредственное интегрирование функций. Интегрирование методами замены переменной и по частям.
Интегрирование рациональных дробей, тригонометрических выражений и иррациональностей.
Определенный интеграл, его основные свойства.
Связь между определенным и неопределенным интегралами. Формула Ньютона-Лейбница. Вычисление определенного интеграла с помощью замены переменной и интегрирования по частям.
Несобственные интегралы,
Приложения определенного интеграла: площадь плоской фигуры, длина дуги, объем тела.
Приближенное вычисление определенного интеграла.
4.1. Неопределенный интеграл
Пусть
функция
![]() является
производной для функции
является
производной для функции![]() ,
т.е.
,
т.е.
![]() .
Тогда
функция
.
Тогда
функция
![]() называетсяпервообразной
функцией
от
называетсяпервообразной
функцией
от
![]() (или для
(или для![]() ).
).
Например,
функция
![]() является
производной для
является
производной для
![]() ,
а
,
а![]() является
первообразной для
является
первообразной для![]() .
.
В курсе интегрального исчисления решается задача о нахождении первообразной для данной функции, т.е. о нахождении функции по заданной ее производной.
Первообразная
у
данной
функции не одна: например,
![]() и
и
![]() .
Если
функция
.
Если
функция![]() имеет первообразные
имеет первообразные![]() и
и![]() ,
то
,
то![]() и
и![]() ,т.е.
,т.е.![]() ,
,![]() ,
и значит,
,
и значит,![]() .
.
Таким образом, любые две первообразные к одной и той же функции отличаются друг от друга на постоянное слагаемое.
Чтобы получить все первообразные для данной функции, надо взять какую-нибудь одну из них и прибавить к ней произвольную постоянную.
Совокупность
всех первообразных к функции![]() называетсянеопределенным
интегралом
от
функции
называетсянеопределенным
интегралом
от
функции
![]() и обозначается
и обозначается![]() .Здесь
.Здесь![]() -
знак интеграла.
-
знак интеграла.
![]() -подынтегральная
функция;
-подынтегральная
функция;
![]() - подынтегральное
выражение.
- подынтегральное
выражение.
Таким
образом, если
![]() ,то
,то![]() ,
и наоборот.
,
и наоборот.
Например,
![]() .
.
Из определения неопределенного интеграла следует, что
![]()
![]() ,
,
т.е. знаки дифференциала и интеграла уничтожают друг друга. Результат вычисления неопределенного интеграла всегда можно проверить, найдя производную от ответа; при этом должна получиться подынтегральная функция.
Простейшие интегралы получаются обращением формул для производных основных элементарных функций.
Например,
из формулы
![]() получаем
получаем![]() .
.
Таким образом, создается таблица основных интегралов (т.и.):
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
| ||
Здесь
![]() -
дифференцируемая
функция.
-
дифференцируемая
функция.
Простейшие свойства неопределенного интеграла вытекают непосредственно из аналогичных свойств производной:
 -т.е.
«интеграл от суммы равен сумме
интегралов»;
-т.е.
«интеграл от суммы равен сумме
интегралов»; -т.е.
«постоянный множитель можно выносить
за знак интеграла».
-т.е.
«постоянный множитель можно выносить
за знак интеграла».
Применяя указанные свойства, некоторые интегралы удается вычислить, представив их в виде суммы табличных интегралов.
Например:
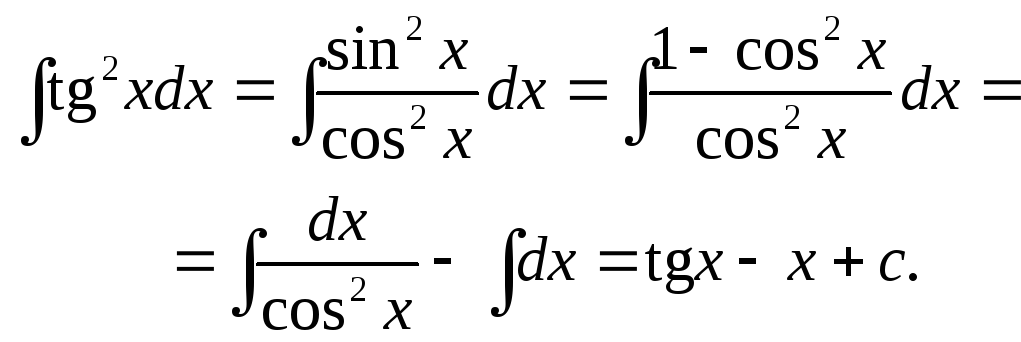
Существует два основных метода интегрирования: по частям и замены переменной.
Рассмотрим сначала метод замены переменной.
Пусть
![]() - некоторая
дифференцируемая функция, тогда формула
замены переменной
- некоторая
дифференцируемая функция, тогда формула
замены переменной
![]() .
.
Эту
формулу можно истолковать так: любая
формула интегрирования вида
![]() сохраняется,
если в подынтегральном выражении и в
правой части формулы сделать произвольную
замену переменной
сохраняется,
если в подынтегральном выражении и в
правой части формулы сделать произвольную
замену переменной
![]() .
В этом
смысле все табличные формулы инвариантны.
.
В этом
смысле все табличные формулы инвариантны.
Пример:
Вычислить интеграл
![]()
Так
как
![]() ,
то
,
то
![]() .
.
(здесь
использовали табличный интеграл
![]() ).
).
В некоторых случаях замена переменной (подстановка) сопровождается преобразованиями.
Пример:
![]()
Применим
подстановку
![]() .
Тогда
.
Тогда![]() ,
,![]() ,откуда
,откуда

![]()
![]()

Интегрирование по частям основано на использовании формулы
![]() .
.
При
применении этой формулы подынтегральная
функция разбивается на два множителя![]() ,
один из
которых интегрируется, а второй -
дифференцируется. При этом в правой
части формулы может получиться
табличный интеграл или интеграл более
простой, чем исходный.
,
один из
которых интегрируется, а второй -
дифференцируется. При этом в правой
части формулы может получиться
табличный интеграл или интеграл более
простой, чем исходный.
Пример:

![]()
![]()
Вообще метод интегрирования по частям применяют к интегралам вида
1.
![]()
2.
![]()
![]()
3.
![]()
За
![]() принимают
трансцендентную функцию, являющуюся
множителем при
принимают
трансцендентную функцию, являющуюся
множителем при![]() ,
,
Пример:

![]()
![]()
![]()
Пример:

![]()
![]()
Последний интеграл справа интегрируем по частям; полагая
![]()
Следовательно,
![]()
Таким образом,
![]()
Откуда
![]() ,
,
![]() .
.
Далее рассмотрим интегрирование некоторых классов функций, начиная с рациональных функций.
Интеграл
от дробно-рациональной функции
![]() ,(
,(![]() и
и![]() -
многочлены)
всегда может быть выражен через
элементарные функции. Среди всех
дробно-рациональных функций выделяют
4 типа простейших дробей:
-
многочлены)
всегда может быть выражен через
элементарные функции. Среди всех
дробно-рациональных функций выделяют
4 типа простейших дробей:



 .
.
Интегралы от простейших дробей существуют и выражаются через элементарные функции.
Рассмотрим
![]() .
.
Если
знаменатель
![]() правильной
рациональной дроби
правильной
рациональной дроби
![]() может
быть представлен в виде
может
быть представлен в виде
![]()
причем все множители, фигурирующие в разложении, различны, а квадратные трехчлены не имеют действительных корней, то
![]()
![]()
![]()
![]()
где
![]()
![]() -
действительные числа, которые нужно
найти. Для их определения обе части
последнего тождества приводят к целому
виду, а затем приравнивают коэффициенты
при одинаковых степенях переменной
-
действительные числа, которые нужно
найти. Для их определения обе части
последнего тождества приводят к целому
виду, а затем приравнивают коэффициенты
при одинаковых степенях переменной![]() ,
что дает систему линейных уравнений
относительно неизвестных коэффициентов.
,
что дает систему линейных уравнений
относительно неизвестных коэффициентов.
В
случае, когда рациональная дробь
![]() неправильная
(т.е. степень многочлена в числителе
больше или равна степени многочлена в
знаменателе), следует предварительно
выделить целую часть.
неправильная
(т.е. степень многочлена в числителе
больше или равна степени многочлена в
знаменателе), следует предварительно
выделить целую часть.
Пример:
![]() .
.
Подынтегральная функция - правильная рациональная дробь. Все корни знаменателя действительные и простые, поэтому подынтегральная функция представима в виде суммы трех простейших дробей первого типа:
![]() ,
,
где
![]() - неопределенные
коэффициенты, которые следует найти.
- неопределенные
коэффициенты, которые следует найти.
Приводя дроби к общему знаменателю и отбрасывая его, получим тождество
![]()
Сравнивая
коэффициенты при одинаковых степенях
![]() в
левой и правой частях тождества, получим
систему уравнений для определения
коэффициентов:
в
левой и правой частях тождества, получим
систему уравнений для определения
коэффициентов:

Решая
эту систему уравнений, найдем
![]() ,
,![]() ,
,![]() .
Следовательно,
.
Следовательно,
![]()
![]()
![]() .
.
Пример:
![]() .
.
Так как степень числителя выше степени знаменателя, т. е. дробь неправильная, то нужно выделить целую часть.
Разделим числитель на знаменатель:

Разложим знаменатель дроби на простейшие множители:
![]()
Следовательно,
![]() .
.
Разложим оставшуюся правильную дробь на сумму простейших дробей:
![]()
![]() .
.
Отсюда
![]() .
.
Найдем
коэффициенты
![]() и
и![]() :
:
![]() ,
,
![]()
![]()
Пример:
![]() .
.
Под знаком интеграла стоит правильная дробь, у которой знаменатель раскладывается на множители вида
![]() .
.
Следовательно, разложение на простейшие дроби имеет вид
![]()
![]() .
.
Отсюда получим тождество
![]() .
.
Приравнивая
коэффициенты при одинаковых степенях
![]() ,
получим систему для определения чисел
,
получим систему для определения чисел![]() ,
,
![]() и
и![]() .
.

Отсюда
![]()
![]()
![]() .
Таким образом,
.
Таким образом,
![]()
![]()
![]() .
.
Пример:
![]() ,
,
![]() ,
причем второй множитель не раскладывается
на линейные множители, т. к. его дискриминант
отрицателен. Подынтегральная функция
представима в виде
,
причем второй множитель не раскладывается
на линейные множители, т. к. его дискриминант
отрицателен. Подынтегральная функция
представима в виде
![]() .
.
Отсюда
![]() .
.
Приравниваем
коэффициенты при одинаковых степенях![]() :
:
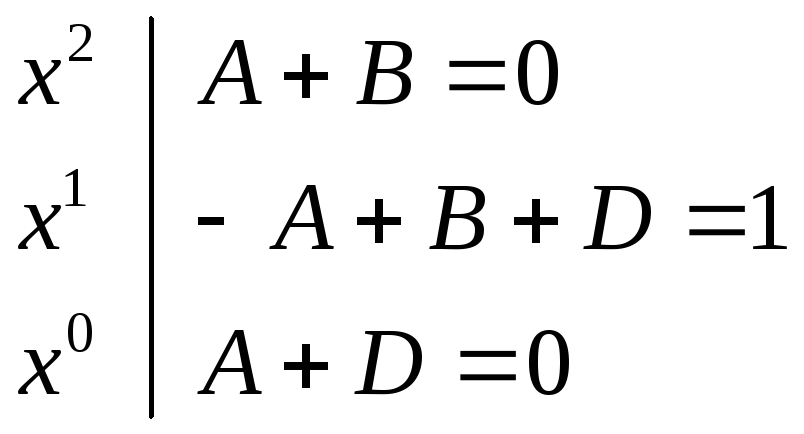
Решая полученную систему относительно неизвестных коэффициентов, получим
![]()
Таким образом,
![]()
Для вычисления интеграла
![]()
выделим в знаменателе полный квадрат:
![]()
и
сделаем подстановку
![]() .
.
Тогда


![]()
Возвращаясь
к переменной
![]() ,
получим
,
получим
![]()
Окончательно получаем
![]() Теперь
рассмотрим интегрирование простейших
иррациональностей.
Теперь
рассмотрим интегрирование простейших
иррациональностей.
1)
Интеграл от функции, рационально
зависящей от дробных степеней
независимой переменной![]() ,
т.е.
,
т.е.
![]() ,
,
сводится
к интегралу от дробно-рациональной
функции с помощью подстановки![]() ,
где
,
где
![]() есть
наименьшее общее кратное чисел
есть
наименьшее общее кратное чисел![]()
2)

вычисляется
с помощью подстановки
![]() ,
,
где
![]() .
.
Пример:
![]() .
.
Используем
подстановку![]() ,
так как
,
так как
![]() ;
;
![]() .
.
Откуда
![]()
![]() .
.
Возвращаясь
к исходной переменной![]() ,
получаем
,
получаем
![]() .
.
Пример:
![]() .
.
Подынтегральное
выражение есть рациональная функция
от
![]() ,
поэтому положим
,
поэтому положим![]() ,
отсюда
,
отсюда![]() ,
,
![]() .
.
Следовательно,
![]()
![]() .
.
Возвращаясь
к переменной![]() ,
получим
,
получим
![]()
![]() .
.
Перейдем к интегрированию некоторых тригонометрических функций.
Интегралы
вида
![]() ,
где
,
где![]() -
рациональная
функция от
-
рациональная
функция от![]() и
и![]() ,
приводятся к интегралам от дробно-рациональных
функций с помощью подстановки
,
приводятся к интегралам от дробно-рациональных
функций с помощью подстановки![]() .
.
Эта подстановка называется универсальной.
При этом
![]()
![]()
Универсальная подстановка часто приводит к слишком громоздким выкладкам. Иногда бывает выгоднее пользоваться более простыми подстановками:
а) если выполняется равенство
![]() ,
,
то
удобнее использовать подстановку
![]() ;
;
б) если выполняется равенство
![]() ,
,
то![]() ;
;
в) если выполняется равенство
![]() ,
,
то
![]() .
.
Пример:
![]() .
.
Положим![]() .
.
Тогда
![]()
![]()
![]()
Отсюда
![]()
Разложим
знаменатель подынтегральной функции
на простейшие множители:
![]() .
.
Разложим подынтегральную функцию на простейшие дроби:
![]()
![]() .
Перейдем
к равенству числителей:
.
Перейдем
к равенству числителей:
![]() .
.
Найдем коэффициенты
![]()
Следовательно,
![]()
![]()
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Пусть
на отрезке
![]() определена функция
определена функция![]() .
.
Интегральной суммой называется
![]() ,
,
где
![]() ,
,
![]() .
.
Определенным
интегралом
от функции
![]() на отрезке
на отрезке![]() называется предел интегральных сумм:
называется предел интегральных сумм:
![]()
при
![]() .
.
Если
этот предел существует, функция называется
интегрируемой на отрезке
![]() .
Всякая
непрерывная функция интегрируема на
конечном промежутке
.
Всякая
непрерывная функция интегрируема на
конечном промежутке![]() .
.
Формулой Ньютона-Лейбница называется формула
![]() ,
,
где
![]() -
одна из
первообразных для функции
-
одна из
первообразных для функции
![]() ,т.е.
,т.е.
![]() .
.
Если
функция
![]() удовлетворяет
следующим условиям:
удовлетворяет
следующим условиям:
1)
![]() -
непрерывно-дифференцируемая однозначная
функция, заданная на отрезке
-
непрерывно-дифференцируемая однозначная
функция, заданная на отрезке![]() ;
;
2)
значения
функции
![]() при
изменении
при
изменении![]() на отрезке
на отрезке![]() не выходят за пределы отрезка
не выходят за пределы отрезка![]() ;
;
3)
![]() ,то
для любой непрерывной на отрезке
,то
для любой непрерывной на отрезке![]() функции
функции
![]() справедлива
формула замены переменной в определенном
интеграле
справедлива
формула замены переменной в определенном
интеграле
![]() .
.
Если
![]() и
и
![]() -
функции от
-
функции от
![]() ,имеющие
непрерывные производные, то
,имеющие
непрерывные производные, то
![]() .
.
Или в более короткой записи:
![]() .
.
Это формулы интегрирования по частям в определенном интеграле.
Пример:
![]() .
.
Пример:
 ,
,
Применим
подстановку
![]() ,
,
откуда![]()
-
0
0

1
![]() .
.
Следовательно,

![]()
В
технических приложениях часто приходится
иметь дело с определенными интегралами,
вычислить которые с помощью формулы
Ньютона-Лейбница или искусственными
приемами практически невозможно. В этом
случае значение интеграла находят
приближенно. Вычислим, например, с
точностью до 0,001 интеграл
![]() .
Применим
для этого формулу Симпсона:
.
Применим
для этого формулу Симпсона:
![]()
![]() ,
,
где
![]() -
четное число;
-
четное число;![]() .
.
Можно показать, что погрешность этой формулы
![]() ,
,
где![]() -наибольшее
значение модуля четвертой производной
интегрируемой функции на отрезке
-наибольшее
значение модуля четвертой производной
интегрируемой функции на отрезке![]() .
Последовательно
дифференцируя четыре раза функцию
.
Последовательно
дифференцируя четыре раза функцию
![]() ,найдем
,найдем
![]() .
.
Легко
видеть, что
![]() и
и![]() .
Далее
очевидно, что производная
.
Далее
очевидно, что производная
![]() возрастает
при
возрастает
при![]() и, следовательно, принимает наибольшее
значение при
и, следовательно, принимает наибольшее
значение при![]() .Итак,
.Итак,
![]() .
.
При
![]() получим
получим
![]() .
.
Таким
образом, погрешность, получающаяся при
использовании формулы Симпсона
![]() для вычисления данного интеграла, не
превосходит 0,00012.
для вычисления данного интеграла, не
превосходит 0,00012.
Вычислим
интеграл по формуле Симпсона
![]() при
при![]() :
:
![]()
![]() .
.
Используя таблицу значений показательной функции (см., например: Бронштейн И.Н., Семендяев К.А.. Справочник по математике - М: Наука, 1980), находим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончательно
получаем![]() .
.
Как
было установлено, в результате применения
приближенной формулы Симпсона погрешность
не превышает 0,00012. Однако еще нельзя
утверждать, что найденное значение
интеграла удовлетворяет условию
задачи, т.е. отличается от истинного
менее чем на 0,001. Дело в том, что
использованные значения
![]() не
точные, а приближенные значения
соответствующих величин (значение
не
точные, а приближенные значения
соответствующих величин (значение![]() является
точным). Каждое из этих значений взято
с четырьмя десятичными знаками, т.е.
отличается от соответствующего истинного
значения
является
точным). Каждое из этих значений взято
с четырьмя десятичными знаками, т.е.
отличается от соответствующего истинного
значения![]() не более чем
на 0,00005. Поэтому погрешность суммы,
заключенной в квадратных скобках,
не превышает
не более чем
на 0,00005. Поэтому погрешность суммы,
заключенной в квадратных скобках,
не превышает
![]()
Перед
этой суммой стоит множитель![]() ,
поэтому погрешность, получающаяся в
результате округления чисел, включая
и погрешность из-за округления результата
деления числа 43,8805 на 30 (эта погрешность
не превышает 0,00033), не превосходит
величины
,
поэтому погрешность, получающаяся в
результате округления чисел, включая
и погрешность из-за округления результата
деления числа 43,8805 на 30 (эта погрешность
не превышает 0,00033), не превосходит
величины
![]()
Таким образом, найденное значение интеграла отличается от истинного его значения не более чем на величину
![]() .
.
Полученный результат удовлетворяет условию задачи.
Теперь перейдем к несобственным интегралам с бесконечными пределами (1 рода).
Пусть
функция
![]() определена для всех
определена для всех![]() и
интегрируема на любом отрезке
и
интегрируема на любом отрезке![]() .
Тогда
.
Тогда
![]() называетсянесобственным
интегралом
от
называетсянесобственным
интегралом
от
![]() в пределах от
в пределах от![]() до
до![]() и
обозначается
и
обозначается![]() .
Аналогично определяются интегралы
.
Аналогично определяются интегралы![]() и
и![]() .
.
Таким образом,
![]() ,
,
![]() ,
,
![]() .
.
Если эти пределы существуют и конечны, то соответствующие интегралы называются сходящимися. В противном случае интегралы называются расходящимися,
Пример. Вычислить несобственный интеграл
![]() .
.
Решение.
По определению
![]()
Пример.
Вычислить
![]() .
.
Решение.
По определению
![]()
(вместо
точки
![]() в
качестве промежуточного предела
интегрирования можно взять любую
другую конечную точку оси
в
качестве промежуточного предела
интегрирования можно взять любую
другую конечную точку оси![]() ).
Вычислим каждый из пределов, стоящих
в правой части написанного выше равенства:
).
Вычислим каждый из пределов, стоящих
в правой части написанного выше равенства:
![]()
![]()
![]() ;
;
![]()
![]() .
.
Следовательно,
![]() .
.
Далее рассмотрим несобственные интегралы от неограниченных функций (II рода).
Если
функция
![]() определена при
определена при![]() ,
интегрируема на любом отрезке
,
интегрируема на любом отрезке![]() и
не ограничена слева от точки
и
не ограничена слева от точки![]() ,
то по
определению полагают
,
то по
определению полагают
![]() .
.
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся. В противном случае интеграл называется расходящимся.
Аналогично,
если функция не ограничена справа от
точки![]() ,
то
,
то
![]()
И,
наконец, если функция
![]() в окрестности внутренней точки
в окрестности внутренней точки![]() не
ограничена, то по определению
не
ограничена, то по определению
![]()
![]() .
.
Пример.
Вычислить
![]() .
.
Решение.
Подынтегральная
функция
![]() не
ограничена в окрестности точки
не
ограничена в окрестности точки![]() .
На любом же отрезке
.
На любом же отрезке![]() она
интегрируема, так как является непрерывной
функцией. Поэтому
она
интегрируема, так как является непрерывной
функцией. Поэтому
![]()
![]() .
.
Пример.
Вычислить
![]() .
.
Решение.
Подынтегральная
функция не ограничена в окрестности
точек
![]() и
и![]() .
.
Поэтому по определению
![]() .
.
Вместо
точки
![]() можно
взять любую другую внутреннюю точку
отрезка
можно
взять любую другую внутреннюю точку
отрезка![]() .
.
Вычислим теперь каждое слагаемое в отдельности
![]()
![]()
![]() .
.
![]()
![]()
Следовательно
![]() .
.
Перейдем теперь к некоторым геометрическим приложениям определенного интеграла.
