
- •Тема 6. Дифференциальные уравнения
- •Однородные дифференциальные уравнения 1-го порядка
- •Линейные дифференциальные уравнения 1-го порядка. Уравнение Бернулли
- •«Дифференциальные уравнения»
- •Контрольные вопросы к экзамену
- •Список рекомендуемой литературы
- •Тема 1. Элементы линейной и векторной алгебры 5
Тема 6. Дифференциальные уравнения
Программный объем темы:
Дифференциальные уравнения 1-го порядка. Задача Коши. Теорема существования и единственности решения задачи Коши. Понятие об особых решениях дифференциальных уравнений. Основные классы уравнений, интегрируемых в квадратурах.
Дифференциальные уравнения высших порядков. Задача Коши. Понятие о краевых задачах для дифференциальных уравнений. Теорема существования и единственности решения задачи Коши. Уравнения, допускающие понижение порядка.
Линейные дифференциальные уравнения с постоянными коэффициентами (однородные и неоднородные). Понятие общего решения. Метод вариации произвольных постоянных.
Линейные дифференциальные уравнения с постоянными коэффициентами с правой частью специального вида.
Задача Коши для нормальной системы дифференциальных уравнений. Теорема существования и единственности решения задачи Коши. Метод исключения. Векторно-матричная запись нормальной системы. Структура общего решения.
Нормальные системы линейных дифференциальных уравнений с постоянными коэффициентами. Решение в случае простых корней характеристического уравнения.
Дифференциальное уравнение 1-го порядка - уравнение, связывающее независимую переменную, искомую функцию и ее первую производную
![]() .
.
Решением
дифференциальных уравнений называется
любая действительная функция![]() ,
определенная
на некотором интервале
,
определенная
на некотором интервале
![]() и обращающая данное уравнение в тождество.
и обращающая данное уравнение в тождество.
Если
функция, являющаяся решением
дифференциального уравнения,
определена в неявном виде:
![]() ,
то
,
то
![]() называется
интегралом данного дифференциального
уравнения.
называется
интегралом данного дифференциального
уравнения.
Рассмотрим некоторые типы дифференциальных уравнений 1-го порядка:
Уравнения с разделяющимися переменными
![]() ,
,
или
![]() .
.
Разделение переменных производится следующим образом:
![]() ,
,
которые интегрируются
![]() ;
;
![]() .
.
Пример. Найти общее решение дифференциального уравнения
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
общий интеграл уравнения.
-
общий интеграл уравнения.
Пример.
Найти частное решение дифференциального
уравнения.
![]() ,
удовлетворяющее начальному условию
,
удовлетворяющее начальному условию![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Общее решение.
Используем начальные условия, определим значение произвольной постоянной:
![]() ,
,
![]() ,
,
![]() .
.
Следовательно, частное решение:
![]() .
.
Однородные дифференциальные уравнения 1-го порядка
Уравнение
![]() называется
однородным, если
называется
однородным, если
![]() -
однородная функция нулевого измерения
относительно своих аргументов, т.е.
-
однородная функция нулевого измерения
относительно своих аргументов, т.е.
![]() .
.
Решение
выполняется с помощью замены
![]() .
.
![]()
и сводится к уравнению с разделяющимися переменными.
Пример.
![]() ,
,
![]() ,
,
замена
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() -
общее решение.
-
общее решение.
Найдем![]() ,
используя начальное условие
,
используя начальное условие
![]()
![]() -
частное решение.
-
частное решение.
Линейные дифференциальные уравнения 1-го порядка. Уравнение Бернулли
Уравнение
![]() ,
линейное относительно неизвестной
функции и ее производной
,
линейное относительно неизвестной
функции и ее производной![]() ,
называется
неоднородным линейным дифференциальным
уравнением первого порядка. Функции
,
называется
неоднородным линейным дифференциальным
уравнением первого порядка. Функции
![]() и
и![]() должны
быть непрерывными на отрезке
должны
быть непрерывными на отрезке![]() для того,
чтобы выполнились условия теоремы
Коши существования и единственности
решения.
для того,
чтобы выполнились условия теоремы
Коши существования и единственности
решения.
Для
решения выполняем замену
![]()
![]() ,
,
![]() ,
,
т.е. общее решение всегда можно записать в виде
![]()
Пример:
![]()
Ищем
решение в виде![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() .
.
Пример:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Уравнение Бернулли
![]() ,
,
замена
![]() приводит
его к линейному.
приводит
его к линейному.
Пример:
![]() или
или
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Пример решения задачи на составления дифференциальных уравнений.
З адача.
Записать уравнения кривой, проходящей
через т.
адача.
Записать уравнения кривой, проходящей
через т.
![]() и обладающей следующим свойством:
площадь треугольника, образованного
радиус-вектором любой точки кривой,
касательной в этой точке и осью абсцисс,
равна 2.
и обладающей следующим свойством:
площадь треугольника, образованного
радиус-вектором любой точки кривой,
касательной в этой точке и осью абсцисс,
равна 2.
Как
видно из рисунка,
![]() .
.
Из
![]() получаем
получаем
![]() ,
,
![]() ,
,
 ,
,
![]() ,
,
![]() .
.
Поставим
в это равенство выражение
![]() и
и![]() и
придем к дифференциальному уравнению
и
придем к дифференциальному уравнению
![]() ,
,
![]() ,
,
![]() -линейное
уравнение 1-го порядка. Решаем его с
помощью подстановки
-линейное
уравнение 1-го порядка. Решаем его с
помощью подстановки
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ответ:
![]() ,
искомая кривая проходит через точку
,
искомая кривая проходит через точку![]() поэтому
поэтому![]() ;
;![]() -данная
кривая гипербола.
-данная
кривая гипербола.
Перейдем теперь к дифференциальным уравнениям 2-го порядка, допускающим понижения порядка.
 -общее
решение такого вида находим методом
2-кратного интегрирования.
-общее
решение такого вида находим методом
2-кратного интегрирования.Пусть дифференциальное уравнение 2-го порядка не содержит искомой функции
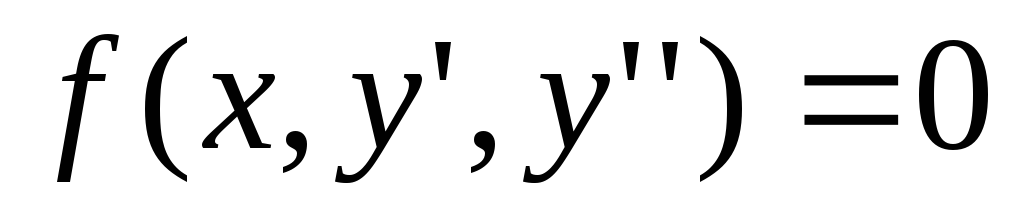 .
.
В
этом случае выполняется замена
![]() и
уравнение становиться уравнением
и
уравнение становиться уравнением![]() первого
порядка.
первого
порядка.
После
нахождения![]() находим
находим![]() .
.
Пример.![]() ,
,
![]() ,
,
![]() -уравнение
1-го порядка с разделяющимися переменными.
-уравнение
1-го порядка с разделяющимися переменными.
![]()
 ,
,
![]() ,
,
![]() .
.
Дифференциальное уравнение 2-го порядка не содержит независимую переменную
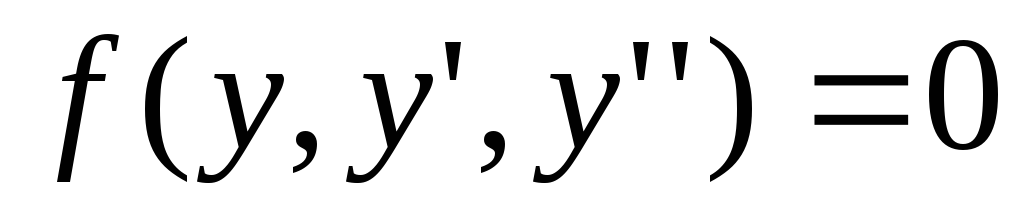 .
.
В этом случае выполняется замена
![]() ,
,
После чего уравнение сводится к уравнению 1-го порядка.
Пример:![]() ,
,
![]() ,
,
![]() .
.
Далее рассмотрим линейные дифференциальные уравнения с постоянными коэффициентами.
![]() -
не-однородное уравнение
-
не-однородное уравнение
![]() -го
порядка.
-го
порядка.
![]() -
однородное уравнение,
-
однородное уравнение,![]() .
.
Составляется характеристическое уравнение
![]() .
.
Пример:
![]()
Характеристическое
уравнение
![]() ,
,
Находятся
его корни:
![]() .
.
Корни характеристического уравнения могут быть:
различные действительные;
действительные равные;
комплексные сопряженные.
Пусть
![]() -
линейное однородное дифференциальное
уравнение 2-го порядка с постоянными
коэффициентами.
-
линейное однородное дифференциальное
уравнение 2-го порядка с постоянными
коэффициентами.
![]() -характеристическое
уравнение.
-характеристическое
уравнение.
1)![]() -действительные,
решение запишется в виде
-действительные,
решение запишется в виде
![]() .
.
2)
![]() -корни
равные, решение имеет вид
-корни
равные, решение имеет вид
![]() .
.
3)
![]() -
решение имеет вид
-
решение имеет вид
![]() .
.
Примеры:
1)![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2)![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3)![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
4)![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Если уравнение с постоянными коэффициентами неоднородное, то его решение состоит из суммы решений: общего решения однородного уравнения и частного решения неоднородного уравнения, которое ищем по виду правой части.
Пусть
![]()
![]() и
и![]() -сonst,
то
-сonst,
то
![]() ,
где
,
где![]() -общее
решение однородного уравнения,
-общее
решение однородного уравнения,![]() -частное решение, которое ищем в
зависимости от вида, а именно:
-частное решение, которое ищем в
зависимости от вида, а именно:
1)![]() ,
,
где
![]() -
число коней характеристического
уравнения, равных 0;
-
число коней характеристического
уравнения, равных 0;
2)
![]() ,
,
где
![]() -
число корней характеристического
уравнения, равных;
-
число корней характеристического
уравнения, равных;
3)![]() ,
,
где
![]() -
число корней характеристического
уравнения, равных
-
число корней характеристического
уравнения, равных![]() ;
;
4)
![]() ,
,
![]() ,
,
где
![]() - число корней характеристического
уравнения, равных
- число корней характеристического
уравнения, равных![]() .
.
![]() и
и![]() многочлены
степени
многочлены
степени![]() ,
где
,
где![]()
![]() .
.
Пример:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
так как
,
так как
![]() ;
;
![]() ,
так как
,
так как
![]() и корень характеристического уравнения
и корень характеристического уравнения![]() ,
то
,
то![]() ,
,
![]() .
.
![]() -решение,
подставляем его в уравнение и находим
неизвестные коэффициенты
-решение,
подставляем его в уравнение и находим
неизвестные коэффициенты
![]() и
и![]() :
:
![]()
![]()
![]() .
.
Подставив![]() ,
,![]() ,
,![]() в
исходное уравнение и приравнивая
коэффициенты в левой и правой частях
при одинаковой степени
в
исходное уравнение и приравнивая
коэффициенты в левой и правой частях
при одинаковой степени![]() ,
получаем систему для нахождения
,
получаем систему для нахождения![]() и
и![]() .
.
![]()
![]()
Записываем решение
![]() .
.
Общим решением уравнения будет
![]() ,т.е.
,т.е.
![]() .
.
Решение дифференциального уравнения методом вариаций
произвольных постоянных
![]() .
.
Решаем соответствующее однородное уравнение
![]() .
.
Общее решение однородного уравнения будет
![]() .
.
Считая,
что
![]() и
и![]() – функции, зависимые от
– функции, зависимые от![]() ,
,
![]() .
.
Определим
![]() и
и![]() из
системы
из
системы

которая для данного уравнения имеет вид

находим
![]() и
и![]() из
этой системы, а затем
из
этой системы, а затем![]() и
и![]() :
:

![]()
![]() ;
;
![]() .
.
Общее
решение будет выглядеть
![]() :
:
![]() .
.
Пример: решить систему дифференциальных уравнений:
 .
.
Продифференцируем
первое уравнение по
![]() :
:
![]() и
заменим
и
заменим![]() из
второго уравнения:
из
второго уравнения:
![]() .
.
Окончательно
![]() ,
,
![]() -однородное
линейное уравнение с постоянными
коэффициентами.
-однородное
линейное уравнение с постоянными
коэффициентами.
![]() .
.
Следовательно, решение
![]() ,
,
из
первого уравнения![]() ,
,
поэтому найдём
![]()
и подставим
![]()
![]() ,
,
![]() .
.
Контрольная работа №6 по теме
