
Домашнее задание МНК Пример выполнения
.doc
Вариант 0
В табл. 1 приведено 40 значений параметров
социологического опроса
![]() и
и
![]() .
Параметр опроса
.
Параметр опроса
![]() является зависимым от параметра
является зависимым от параметра
![]() (например,
(например,
![]() – заработная плата,
– заработная плата,
![]() – возраст опрашиваемого). Т.о. дано 40
точек на плоскости
– возраст опрашиваемого). Т.о. дано 40
точек на плоскости
![]() .
.
Таблица 1
|
|
1,483 |
9,840 |
5,603 |
5,126 |
1,251 |
5,734 |
4,794 |
2,288 |
0,087 |
4,958 |
|
|
20,35 |
-51,17 |
1,89 |
7,06 |
15,48 |
1,17 |
8,72 |
17,52 |
17,37 |
8,63 |
|
|
0,078 |
2,045 |
9,286 |
5,329 |
8,580 |
2,844 |
9,168 |
7,860 |
1,678 |
6,095 |
|
|
13,71 |
18,30 |
-47,14 |
4,68 |
-40,56 |
16,60 |
-52,52 |
-23,60 |
17,03 |
-2,18 |
|
|
3,265 |
5,180 |
3,923 |
3,088 |
2,919 |
4,962 |
0,980 |
9,550 |
8,304 |
5,498 |
|
|
19,74 |
4,69 |
11,21 |
18,91 |
17,60 |
6,29 |
20,69 |
-53,60 |
-30,86 |
3,48 |
|
|
9,634 |
4,086 |
0,930 |
4,642 |
4,336 |
9,326 |
8,580 |
3,658 |
2,281 |
1,886 |
|
|
-57,32 |
11,33 |
17,47 |
9,32 |
12,51 |
-42,70 |
-28,18 |
17,97 |
21,76 |
16,89 |
Необходимо:
1)
Перенесем данные табл. 1. в MS Excel.
2)
Произведем сортировку исходных данных. Для этого в MS Excel запишем их в виде двух строк. Отсортированные данные представим в виде табл. 1.1.
Таблица 1.1
|
|
0,078 |
0,087 |
0,93 |
0,98 |
1,251 |
1,483 |
1,678 |
1,886 |
2,045 |
2,281 |
|
|
13,71 |
17,37 |
17,47 |
20,69 |
15,48 |
20,35 |
17,03 |
16,89 |
18,3 |
21,76 |
|
|
2,288 |
2,844 |
2,919 |
3,088 |
3,265 |
3,658 |
3,923 |
4,086 |
4,336 |
4,642 |
|
|
17,52 |
16,6 |
17,6 |
18,91 |
19,74 |
17,97 |
11,21 |
11,33 |
12,51 |
9,32 |
|
|
4,794 |
4,958 |
4,962 |
5,126 |
5,18 |
5,329 |
5,498 |
5,603 |
5,734 |
6,095 |
|
|
8,72 |
8,63 |
6,29 |
7,06 |
4,69 |
4,68 |
3,48 |
1,89 |
1,17 |
-2,18 |
|
|
7,86 |
8,304 |
8,58 |
8,58 |
9,168 |
9,286 |
9,326 |
9,55 |
9,634 |
9,84 |
|
|
-23,6 |
-30,86 |
-40,56 |
-28,18 |
-52,52 |
-47,14 |
-42,7 |
-53,6 |
-57,32 |
-51,17 |
3)
Изобразим заданные точки на рис. 1. График строим по сортированным данным.
4)
Найдем наибольшее и наименьшее значения
аргумента
![]() и функции
и функции
![]() .
.
![]() ,
, ![]() ;
;
![]() ;
; ![]() .
.
5)
Определим средние арифметические аргумента и функции.
![]() ;
; ![]() .
.

Рис. 1.
6)
Найдем сумму всех значений аргумента всех значений функции:
 ;
;
 .
.
7)
Произведем разбивку исходных данных
на интервалы по значениям функции
![]() .
Шаг интервала определим по формуле:
.
Шаг интервала определим по формуле:
 .
.
Для удобства в качестве шага возьмем
значение
![]() .
Опять же для удобства нижнюю границу
первого интервала примем равной
.
Опять же для удобства нижнюю границу
первого интервала примем равной
![]() .
Получаем следующие интервалы по
.
Получаем следующие интервалы по
![]() :
:
интервал 1:
![]() ;
;
интервал 2:
![]() ;
;
интервал 3:
![]() ;
;
интервал 4:
![]() ;
;
интервал 5:
![]() ;
;
интервал 6:
![]() ;
;
интервал 7:
![]() .
.
Верхняя граница последнего интервала
превышаем максимальное значение функции
![]() ,
следовательно, разбивку на интервалы
прекращаем.
,
следовательно, разбивку на интервалы
прекращаем.
8)
Определим количество пар чисел
![]() и
и
![]() (точек), попадающее в каждый из рассмотренных
интервалов. Для этого используем в MS
Excel функцию ЧАСТОТА.
(точек), попадающее в каждый из рассмотренных
интервалов. Для этого используем в MS
Excel функцию ЧАСТОТА.
9)
Найдем суммарное значение функции
![]() для каждого интервала, а также среднее
арифметическое значение параметра
для каждого интервала, а также среднее
арифметическое значение параметра
![]() для каждого интервала (используя функцию
СУММЕСЛИ).
для каждого интервала (используя функцию
СУММЕСЛИ).
10)
Сведем все полученные для интервалов данные в табл. 2.
|
№ Интервала |
Интервал по
|
Число точек,
|
Сумма значений
|
Среднее
значение
|
|
1 |
от –57,5 до –46,0 |
5 |
–261,75 |
–52,35 |
|
2 |
от –46,0 до –34,5 |
2 |
–83,26 |
–41,63 |
|
3 |
от –34,5 до –23,0 |
3 |
–82,64 |
–27,55 |
|
4 |
от –23,0 до –11,5 |
0 |
0 |
0,00 |
|
5 |
от –11,5 до 0,0 |
1 |
–2,18 |
–2,18 |
|
6 |
от 0,0 до 11,5 |
12 |
78,47 |
6,54 |
|
7 |
от 11,5 до 23,0 |
17 |
299,9 |
17,64 |
|
Сумма |
40 |
–51,46 |
|
|
11)
Построим гистограмму и график по интервалам и количеству точек, заданным в табл. 2. Представим их на рис. 2.

Рис. 2.
12)
Произведем сглаживание данных табл. 1
методом наименьших квадратов по
уравнению:
![]() .
.
Составляем функцию
![]() для зависимости
для зависимости
![]() :
:
 ,
,
где
![]() – число точек.
– число точек.
Для нахождения экстремума данной функции составляем систему уравнений:

После преобразований получим:

По данным табл. 1. в виде двух строк вычисляем:
![]() ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
В итоге система имеет вид:

Решаем данную систему методом обратной матрицы:
Откуда
![]() ,
,
![]() ;
;
![]() .
.
Сглаживающая функция имеет вид
![]() .
.
13)
Подсчитаем значения
![]() для каждой точки
для каждой точки
![]() табл. 1. и найдем сумму всех
табл. 1. и найдем сумму всех
![]() –
–
![]() .
.
14)
Определим квадрат разницы значений
![]() табл.1. и сглаженных
табл.1. и сглаженных
![]() для каждой точки
для каждой точки
![]() .
.
15)
Найдем сумму всех квадратов разницы –
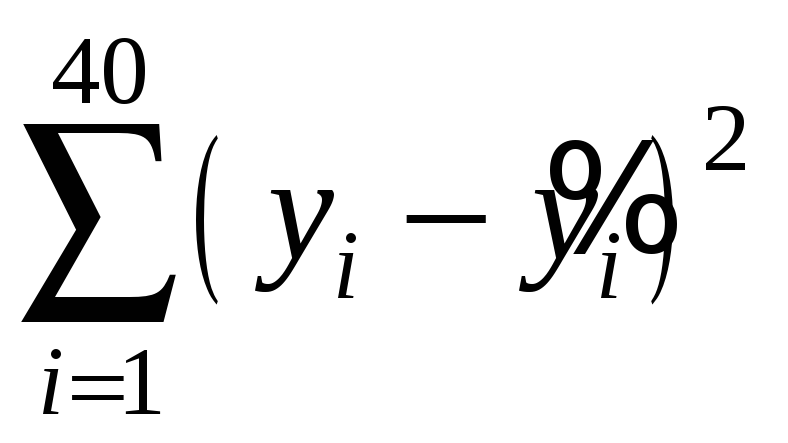 .
.
16)
На Диаграмме 1 изобразим график сглаженной
кривой
![]() и нанесем линию тренда в виде полиномиальной
функции 6-й степени с указанием ее
уравнения на Диаграмме. Все это представим
на рис. 2.
и нанесем линию тренда в виде полиномиальной
функции 6-й степени с указанием ее
уравнения на Диаграмме. Все это представим
на рис. 2.

Рис. 2.
