3. Основные формулы Электростатика. Электрический ток

1. Закон Кулона

,

где - сила, с которой зарядq₁ действует на заряд q₂; - равная ей и противоположно направленная сила;- радиус – вектор, направленный отq₁ к q₂, а r - модуль ;- диэлектрическая проницаемость среды;Е₀ – напряженность электростатического поля в вакууме; Е – напряженность электростатического поля внутри однородного диэлектрика; ₀ - электрическая постоянная.

2. Напряженность электрического поля и потенциал

где W_п - потенциальная энергия положительного точечного заряда q, находящегося в данной точке поля.

Сила, действующая на точечный заряд q, находящийся в электрическом поле, и потенциальная энергия этого заряда

; W_п = q.

3. Напряженность и потенциал поля, создаваемого точечным зарядом q

где r - расстояние от заряда q до точки, в которой определяются напряженность или потенциал.

4. Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции полей).

где _i , _i - напряженность и потенциал в данной точке поля, создаваемого i-м зарядом.

5. Напряженность и потенциал поля, создаваемого сферой радиусом R на расстоянии r от центра сферы:

а)

б)

в)

где q - заряд сферы.

6. Линейная плотность заряда: или  = q/l.

Поверхностная плотность заряда: или = q/S.

Объемная плотность заряда: или=q/V.

Связь заряда и плотностей: dq = dS = d l= dV.

7. Напряженность и потенциал поля, создаваемого распределенными зарядами. Если заряд равномерно распределен вдоль линии с линейной плотностью , то на линии выделяется малый участок длиной dl с зарядом dq = dl. Такой заряд можно рассматривать как точечный и применять формулы:

где - радиус-вектор, направленный от выделенного элементаdl к точке, в которой вычисляется напряженность, а r – его модуль.

Используя принцип суперпозиции электрических полей, находим интегрированием напряженность и потенциал поля, создаваемого распределенным зарядом:

Интегрирование ведется вдоль всей длины l заряженной линии.

8. Напряженность поля, создаваемого бесконечно прямой равномерно заряженной линией или бесконечно длинным цилиндром,

где r - расстояние от нити или оси цилиндра до точки, в которой определяется напряженность поля.

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью,

.

9. Электрическое смещение (электрическая индукция)

.

Теорема Гаусса:

или .

10. Связь потенциала с напряженностью:

а) илив общем случае, где,,- единичные векторы вдоль осей координат (орты);

б)в случае однородного поля;

в) в случае поля, обладающего центральной или осевой симметрией.

11. Электрический момент диполя

,

где q – заряд; l - плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).

12. Работа сил поля по перемещению заряда q из точки поля с потенциалом ₁, в точку с потенциалом ₂

.

13. Электроемкость уединенного тела и конденсатора

С = , С = ,

где  - потенциал проводника; U - разность потенциалов пластин конденсатора.

Следует помнить, что при изменении электрической емкости конденсатора, подключенного к источнику напряжения, меняется величина заряда на его пластинах, а разность потенциалов остается постоянной и равной э.д.с. источника тока. При изменении емкости конденсатора, отключенного от источника напряжения, меняется разность потенциалов на его пластинах, а величина заряда остается при этом неизменной.

Электроемкость плоского конденсатора

C = ,

где S - площадь одной пластины конденсатора; d - расстояние между пластинами.

Электроемкость батареи конденсаторов:

а) при последовательном соединении;

б) при параллельном соединении,

где N- число конденсаторов в батарее.

Энергия заряженного конденсатора:

W = qU/2 =CU²/2 = q²/(2C),

,

где V – объем конденсатора.

Объемная плотность энергии электрического поля:

.

14. Сила тока

где q - заряд, прошедший через поперечное сечение проводника за время t.

Плотность тока

j = I/S,

где S - площадь поперечного сечения проводника.

Связь плотности тока со средней скоростью упорядоченного движения заряженных частиц

,

где q - заряд частиц; n – их концентрация.

15. Закон Ома:

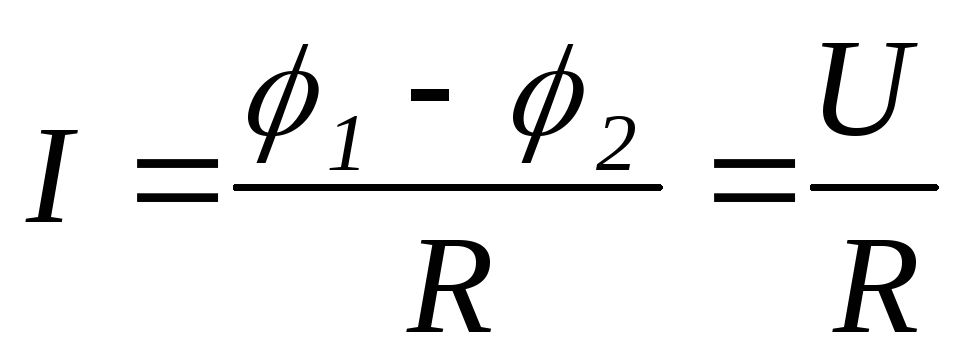1. для участка цепи, не содержащего э.д.с. (для однородного участка цепи), где ₁ - ₂ = U - разность потенциалов (напряжение) на концах участка цепи; R - сопротивление участка;

б) для участка цепи, содержащего э.д.с. (для неоднородного участка цепи), где - э.д.с. источника тока; R - полное сопротивление участка (сумма внешних и внутренних сопротивлений). Знаки «+» или «–» выбираются в зависимости от полярности включения источника.

в) для замкнутой (полной) цепи, гдеR - сопротивление внешней цепи, r - сопротивление внутреннее (сопротивление источника тока).

16. Правила Кирхгофа:

а) - первое правило;

б) - второе правило,

где - алгебраическая сумма сил токов, сходящихся в узле; - алгебраическая сумма произведений сил токов на сопротивления участков замкнутого контура;- алгебраическая сумма э.д.с. в замкнутом контуре.

17. Сопротивление R и проводимость G однородного проводника

R =, G =,

где  - удельное сопротивление;  - удельная проводимость; l - длина проводника; S - площадь поперечного сечения.

Зависимость удельного сопротивления от температуры

,

где α – температурный коэффициент сопротивления, t – температура по шкале Цельсия.

Сопротивление системы проводников;

а) - при последовательном соединении;

б) - при параллельном соединении,

где R_i - сопротивление i - го проводника.

18. Работа тока:

.

Закон Джоуля-Ленца (тепловое действие тока):

где dQ – количество теплоты, выделяющейся в проводнике, dt – промежуток времени, в течение которого выделялось тепло.

Мощность тока полной цепи:

P = I ε.

Мощность тока на внешнем участке цепи:

P = IU = I²R = U²/R.

Закон Ома в дифференциальной форме

.

Закон Джоуля-Ленца в дифференциальной форме

w = γ E²,

где w - объемная плотность тепловой мощности (количество тепла, выделяющегося в единице объема за единицу времени).