4. Определите электрическую емкость плоского конденсатора с двумя слоями диэлектриков: фарфора () толщиной и эбонита () толщиной , если площадь пластин .

Дано: Решение:

Слоистый конденсатор можно представить в виде двух последовательно 

соединенных конденсаторов  и  с расстояниями между обкладками

 и  и площадью обкладок  . Электроемкости этих конденсаторов равны

; , где - электрическая постоянная.

При последовательном соединении конденсаторов ёмкость определяется как:

;

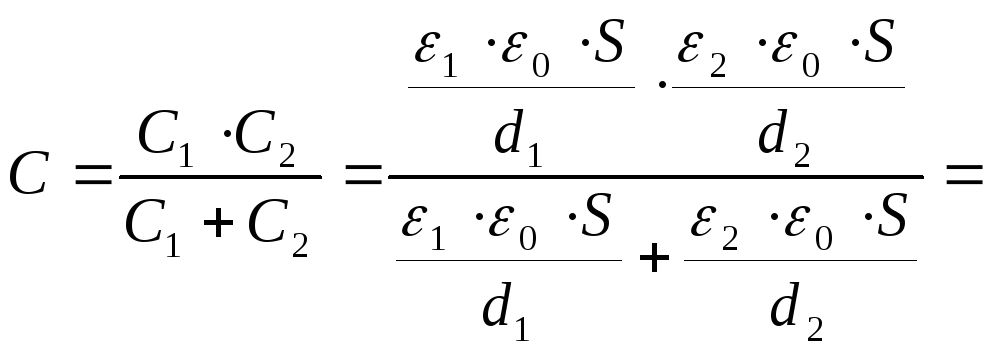
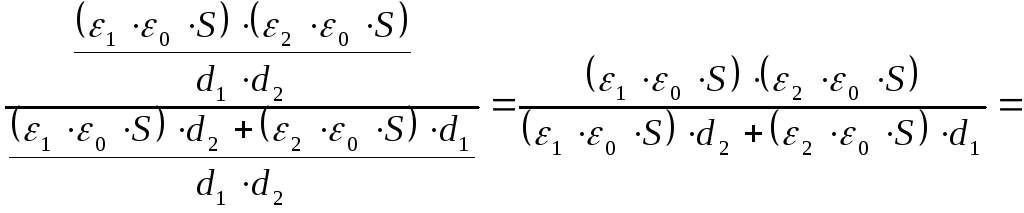
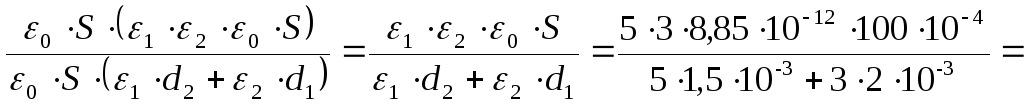
. Ответ: .

5. Определите внутреннее сопротивление источника тока, имеющего ЭДС 1,1 , если подключенный к его зажимам вольтметр показал 1 при сопротивлении внешней цепи в 2 .

Дано: Решение:

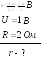По закону Ома для полной цепи: . По закону Ома для участка цепи:

; ; ; ;

; .

Ответ: .

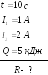
6. В проводнике за время при равномерном нарастании силы тока от до выделилось количество теплоты . Найдите сопротивление проводника.

Дано: Решение:

Количество теплоты, выделяющееся в проводнике при прохождении тока за

время по закону Джоуля-Ленца равно: . Зависимость тока от

времени выражается формулой: ; . Следовательно:

;

.

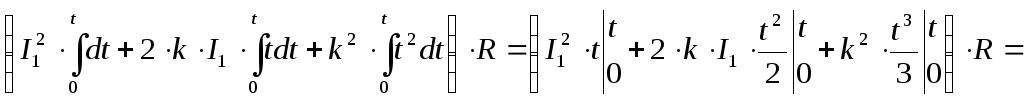
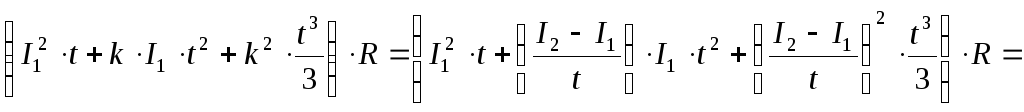
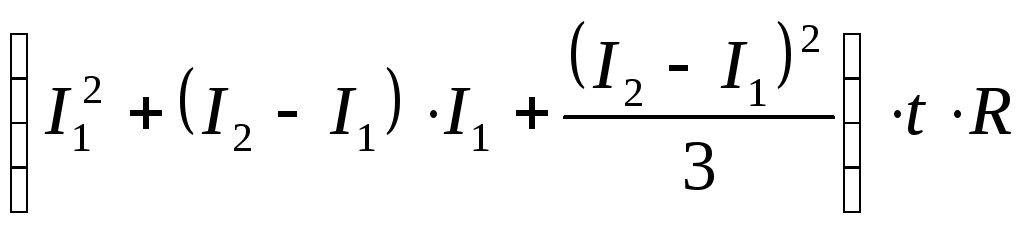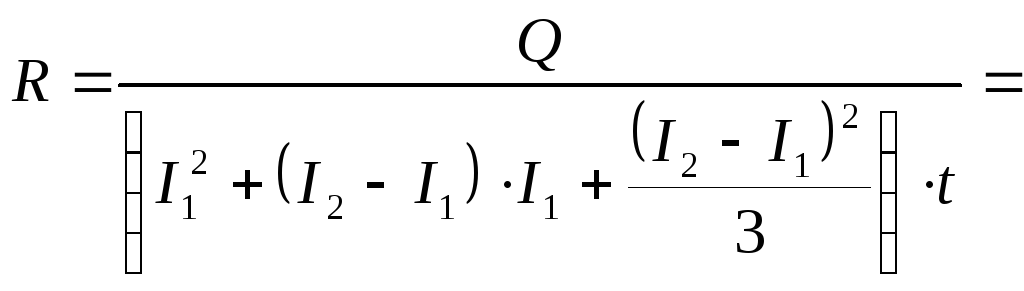
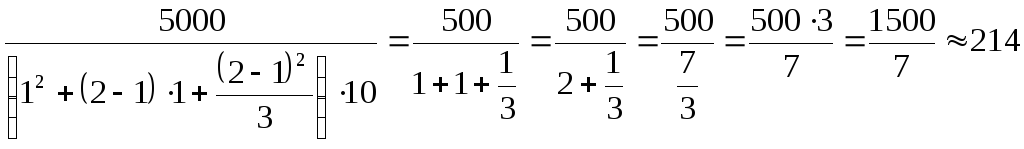
Ответ: .

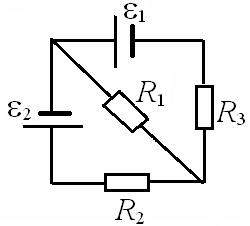
7. В схеме (см. рис.) , , , , . Найдите силу тока во всех участках цепи. Внутренним сопротивлением элементов пренебречь.

Дано: Решение:

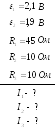
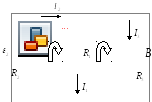
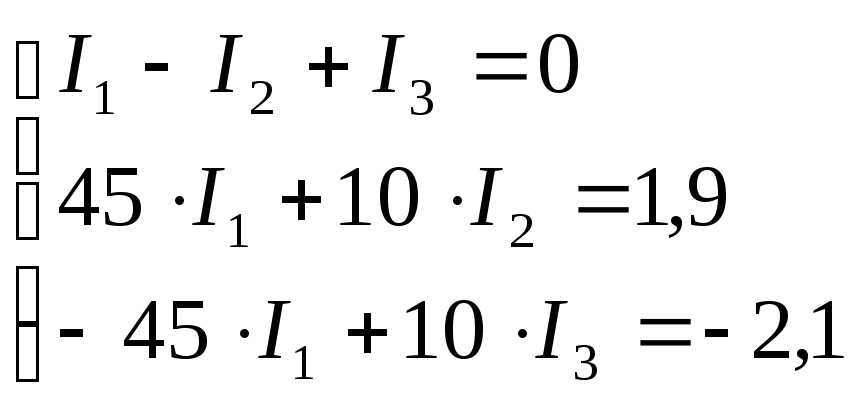. Решим систему методом Крамера:

;

;

;

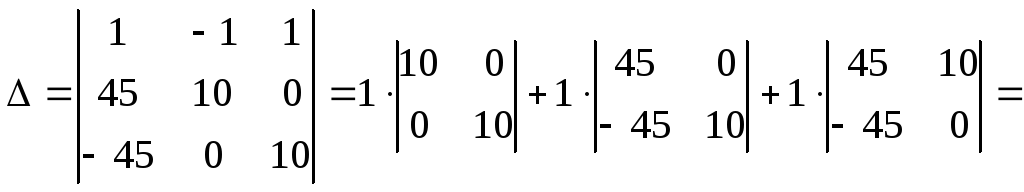
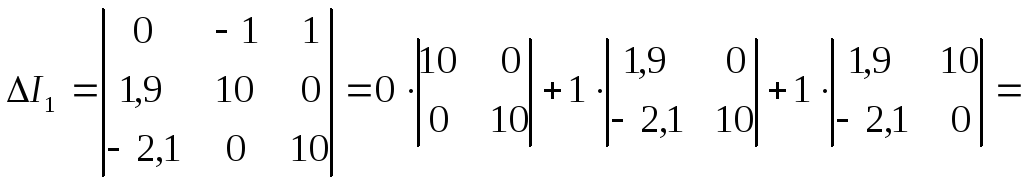
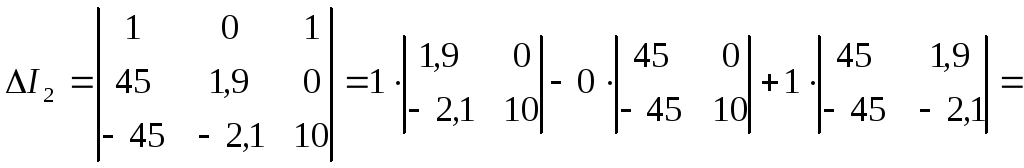
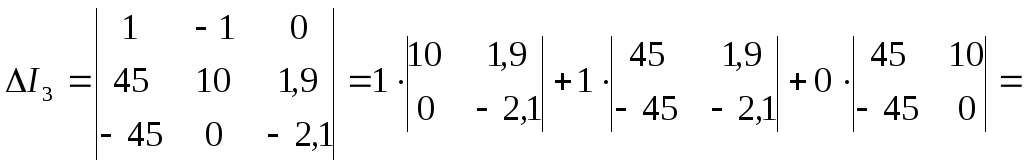
. Следовательно:

; ; .

Проверка:

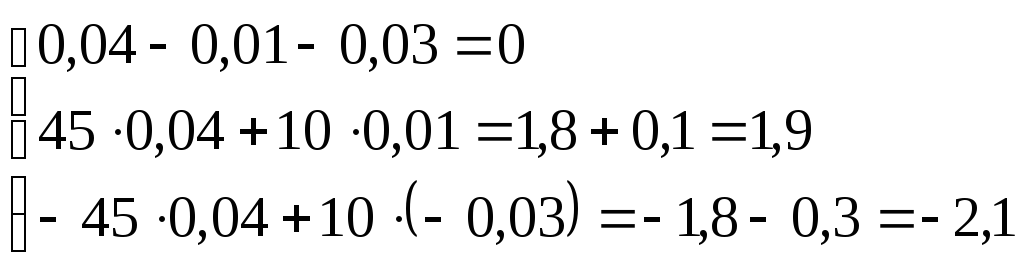
Согласно первому закону Кирхгофа сумма токов, входящих в узел равна нулю:

;. Ток течёт в противоположном направлении. Ответ: ; ; .

Контрольная работа № 3. Магнетизм. Волновая оптика

Вариант 3

1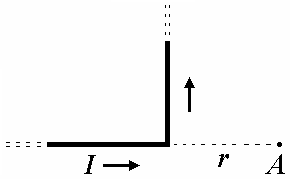. Бесконечно длинный провод согнут под прямым углом. По проводу течет ток (см. рис.). Какова магнитная индукция в точке , если ?

Дано: Решение:

Изогнутый провод с током, при определении параметров, создаваемого им

магнитного поля, целесообразно представить в виде двух проводников, концы

которых соединены в точке перегиба. Вектор магнитной индукции в заданной

точке определится в виде суммы векторов и полей, создаваемых

отрезками длинных проводников, составляющих угол  90.

Вектор магнитной индукции обусловленный током в горизонтальной части

проводника в соответствие с законом Био-Савара-Лапласа определится

соотношением , то есть его модуль равен нулю, так как

продолжение проводника пересекает заданную точку. Модуль магнитной

индукции определим по формуле: , где

  , , - магнитная постоянная. Следовательно:

. Ответ : .

2. На двух легких проводящих нитях горизонтально висит металлический стержень длиной 0,25 и массой 15 . Стержень находится в вертикальном однородном магнитном поле с индукцией 0,3 , силовые линии которого направлены вертикально вниз. Определите угол отклонения нитей, если по стержню пропустить ток 0,2 .

Дано: Решение:

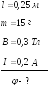
На проводник с током в магнитном поле действуют сила тяжести , сила

натяжения нити , и сила Ампера . Нить отклонилась на угол от

вертикали и находится в равновесии. Условие равновесия по первому закону

Ньютона имеет вид: . Спроектируем силы на оси и .

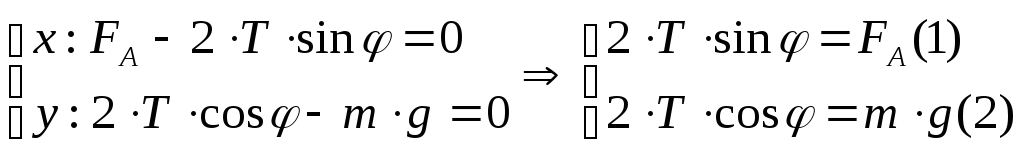. Разделим (1) на (2):

; . Сила Ампера равна: . Так как

стержень находится в вертикальном однородном магнитном поле, то

; ; ;

. Ответ: .

3. Квадратный контур со стороной , в котором течет ток , находится в магнитном поле () под углом к линиям индукции. Какую работу нужно совершить, чтобы при неизменной силе тока в контуре изменить его форму на окружность?

Д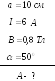ано: Решение:

Площадь квадратного контура со стороной равна: . Виток площадью

, по которому течёт ток обладает магнитным моментом: . В

магнитном поле магнитный момент обладает потенциальной энергией:

. Следовательно: . Периметр

квадратной рамки равен: . При изменении формы квадратного контура

на окружность, периметр стал равен: ; ;

радиус круга. Площадь круга равна: .

Магнитный момент такого контура равен: . В магнитном

поле магнитный момент обладает потенциальной энергией:

. Следовательно, совершенная работа

равна:

. Так как работа отрицательна, то её нужно совершать над контуром

Ответ: .

4. Очень короткая катушка содержит витков тонкого провода. Катушка имеет квадратное сечение со стороной . Найдите магнитный момент катушки при силе тока .

Д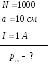ано: Решение:

Магнитный момент катушки равен: . Так как катушка имеет

квадратное сечение, то . Следовательно:

. Ответ: .

5. В проволочной рамке площадью 100 возбуждается ЭДС индукции с амплитудой . Число витков в рамке 200. Рамка вращается с постоянной частотой в однородном магнитном поле, индукция которого . В начальный момент времени плоскость рамки перпендикулярна вектору . Определите ЭДС индукции в рамке спустя 0,1 .

Д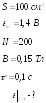ано: Решение:

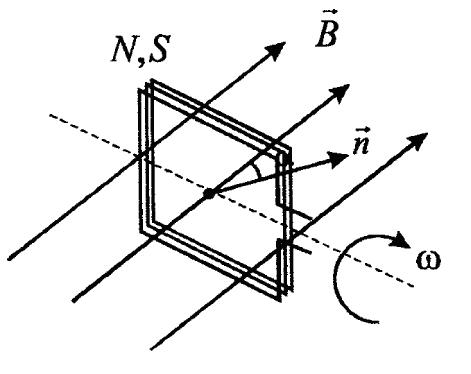
Рамка вращается с некоторой циклической частотой. Угол, составляющий

нормаль к рамке с вектором магнитной индукции со временем меняется по

закону: . Так как в начальный момент времени рамка

перпендикулярна вектору магнитной индукции , то ; .

Магнитный поток через один виток рамки меняется по закону:

. По закону электромагнитной индукции ЭДС одного витка

равна: .

ЭДС рамки равна: , где -

амплитуда ЭДС; ; . При :

.

Ответ: .

6. Катушка с железным сердечником имеет площадь поперечного сечения и число витков . Индуктивность катушки с сердечником при токе через обмотку . Найдите магнитную проницаемость железного сердечника.

Д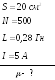ано: Решение:

Потокосцепление связано с током соотношением: . Для

многовитковой катушки потокосцепление равно: ; ;

. Магнитный поток, пронизывающий поперечное сечение катушки,

равен: ; .

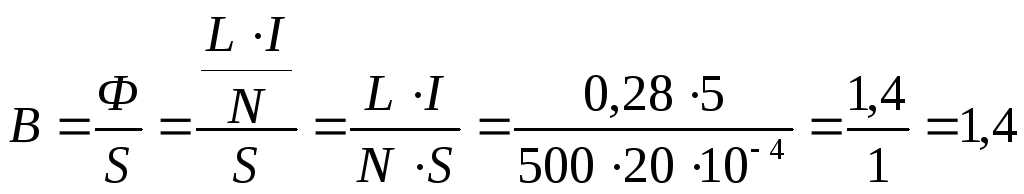
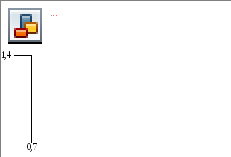
Рис.1. График зависимости индукции от напряженности магнитного поля

По графику зависимости индукции от напряженности магнитного поля

получаем: . Индукция магнитного поля связана с напряжённостью

соотношением: , где - магнитная постоянная.

Следовательно: .

Ответ: .

7. Под каким углом должен падать луч на поверхность стекла (), чтобы угол преломления был в 2 раза меньше угла падения?

Дано: Решение:

Углы падения и преломления связаны соотношением:

; ; ;

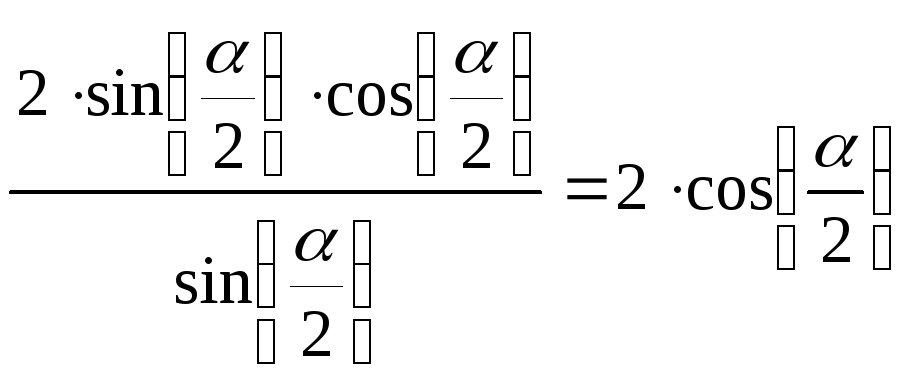. Ответ: .

8. Установка для получения колец Ньютона освещается белым светом, падающим нормально. Найдите радиус 4-го синего кольца (). Наблюдение производится в проходящем свете. Радиус кривизны линзы равен 5 .

Дано: Решение:

Радиус темного кольца в проходящем свете определяется по формуле:

, где - показатель преломления воздуха.

.

Ответ: .

9. Свет с интенсивностью падает на непрозрачный диск, перекрывающий одну зону Френеля. Найдите отношение интенсивности в центре дифракционной картины и .

Р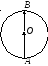ешение:

Из рис. радиус окружности равен амплитуде волны в точке наблюдения в отсутствии экрана. Обозначим этот радиус . Тогда: . Вектор, равный амплитуде колебания, приходящего в точку наблюдения от первой зоны

Френеля, заканчивается в точке . Величина этого вектора равна: . Интенсивность световой волны, приходящей в точку наблюдения от первой зоны: . Следовательно: . Ответ: .

10. Угол максимальной поляризации при отражении света от кристалла каменной соли равен . Определите скорость света в кристалле каменной соли.

Дано: Решение:

Угол падения, при котором отраженный луч полностью поляризован, называется

углом Брюстера и определяется соотношением: ; ; ;

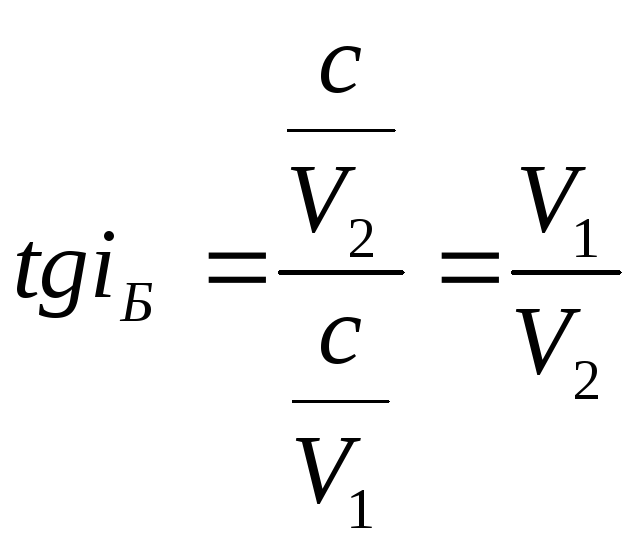. Так как первая среда воздух, то ; ; ;

. Ответ: .