Контрольная работа № 1. Механика и молекулярная физика
1. Какова была
скорость тела в начальный момент времени,
если, двигаясь с постоянным ускорением
2
,
за 3
тело прошло путь 60
?
Д
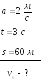ано:
Решение:
Перемещение тела при равноускоренном движении имеет вид:
;
;
.
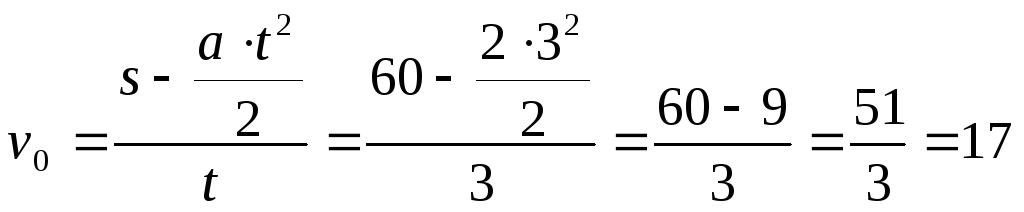
Ответ:
.
2. В лифте, опускающемся
с ускорением 3
,
находится человек массой 60
.
Найдите вес человека.
Д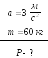
ано:
Решение:
Так как скорость лифта направлена в ту же сторону, что и ускорение, то вес
человека
уменьшается на величину
.
Следовательно:
.
Ответ:
.
3. Молот массой
падает
на поковку, масса которой вместе с
наковальней
.
Скорость молота в момент удара равна 2
.
Найдите энергию, затраченную на сотрясение
(движение) фундамента. Удар молота о
поковку считать неупругим.
Д
ано:
Решение:
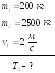1) В
момент удара кинетическая энергия
молота равна:
.
2) Найдём скорость системы «молот-поковка» с наковальней. Применим закон
сохранения импульса для неупругого удара двух тел:
,
где
-
скорость поковки вместе с наковальней
перед
ударом;
-
скорость молота и поковки вместе с
наковальней после удара.
Поковка
с наковальней до удара находилась в
состоянии покоя, то есть
.
Следовательно:
;
.
В результате сопротивления
фундамента
скорость
гасится. Кинетическая энергия системы
«молот-
поковка» с наковальней передаётся фундаменту. Эта энергия находится по
формуле:
.
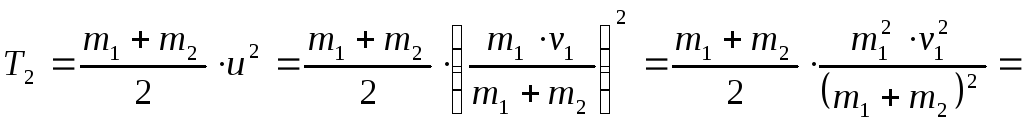
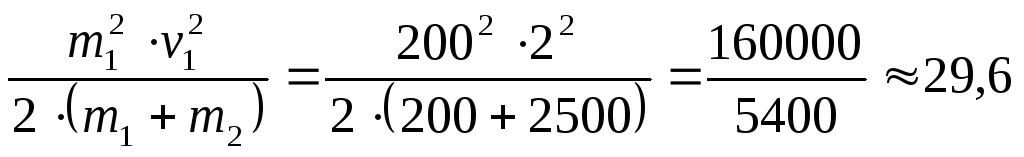
Ответ:
.
4. К ободу однородного
диска радиусом 0,8
и массой 10
приложена постоянная касательная сила
.
При вращении на диск действует момент
сил трения
.
Угловое ускорение, с которым вращается
диск
.
Определите силу
.
Д
ано:
Решение:
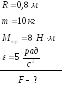Уравнение
движения диска в векторной форме имеет
вид:
,
где
-
момент силы,
- момент
инерции диска
относительно оси вращения. В проекции
на ось
:
;
;
.
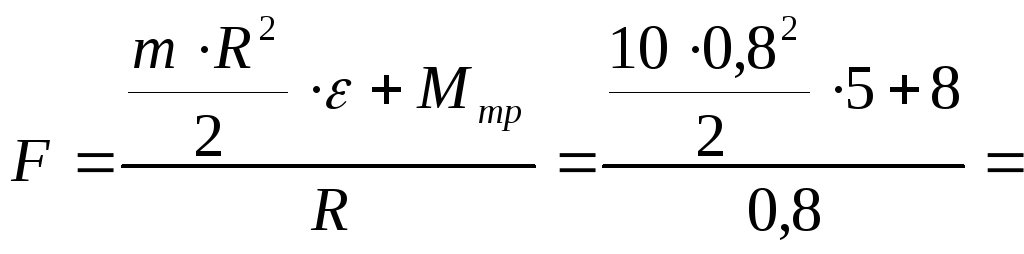
Ответ:
.
5. Диск массой 1
и диаметром 50
вращается вокруг оси, проходящей через
центр перпендикулярно его плоскости,
делая 20
.
Какую работу надо совершить, чтобы
остановить диск?
Д
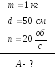ано:
Решение:
Работа сил торможения равна изменению кинетической энергии диска:
.
В момент торможения
;
.
Кинетическая энергия вращающегося
диска равна:
,
где
- момент инерции
диска относительно оси вращения. Угловая скорость связана с частотой
вращения
формулой:
;
.
Следовательно:
.
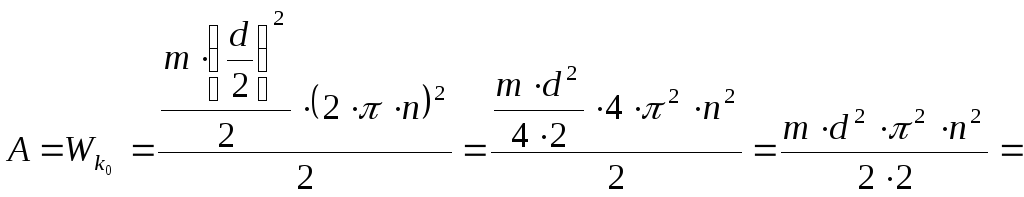
Ответ:
.
6. Амплитуда
гармонических колебаний 5
,
период 4
.
Найдите максимальную скорость колеблющейся
точки и максимальное ускорение.
Д
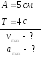ано:
Решение:
Запишем уравнение
колебаний в виде:
.
Скорость колеблющейся точки равна:
.
Ускорение колеблющейся точки равно:
.
Циклическая частота связана с периодом
колебаний
формулой:
.
Максимальная скорость равна:
.
Максимальное ускорение равно:
Ответ:
;
.
7. Диск радиусом
75
колеблется около горизонтальной оси,
проходящей на расстоянии 50
от оси диска перпендикулярно к плоскости
диска. Определите частоту
колебаний
такого физического маятника.
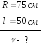Дано:
Решение:
Частота и период
колебаний – обратные величины:
;
.
Период
колебаний физического
маятника равен:
,
где
-
момент
инерции диска относительно произвольной оси, параллельной оси вращения, по
теореме
Гюйгенса-Штейнера равен:
;
-
момент инерции
диска
относительно оси вращения.
;
;
.
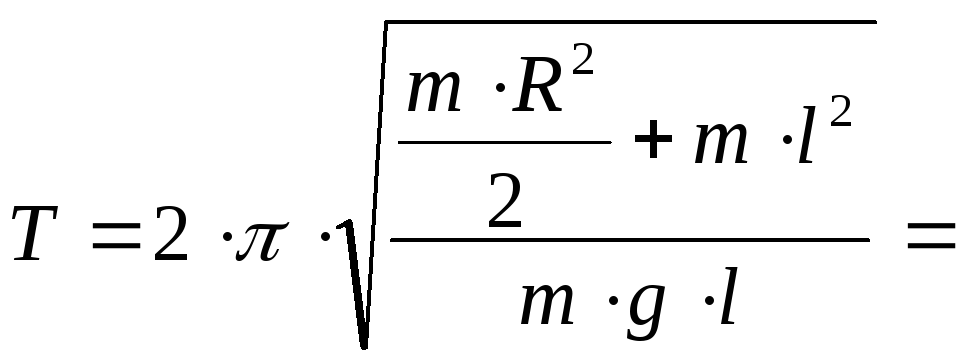
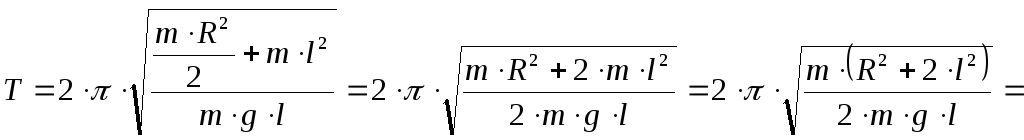
Ответ:
.
8. От источника
колебаний распространяются волны вдоль
прямой линии. Амплитуда колебаний 5
.
Каково смещение точки, удаленной от
источника на 3/4 длины волны в момент,
когда от начала колебаний источника
прошло время, равное 0,5 периода колебаний?
Д
ано:
Решение:
Уравнение
бегущей волны имеет вид:
;
;
.
Следовательно, смещение точки равно:
.
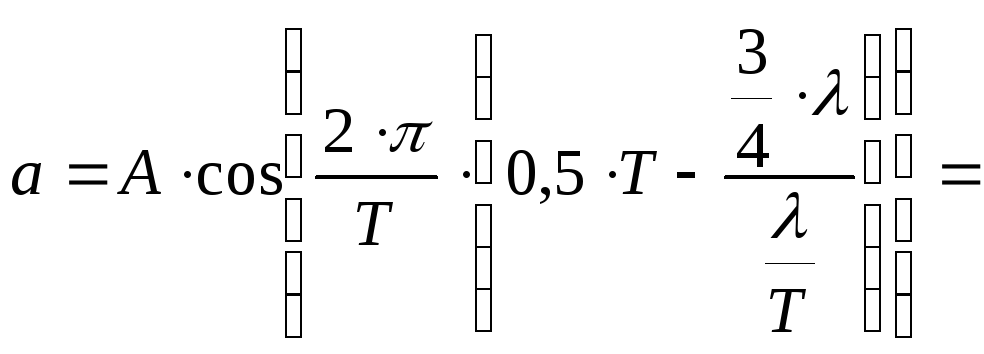
Ответ:
.
9. Сколько молекул
газа содержится в баллоне емкостью
при температуре
и давлении
?
Д
ано:
Решение:
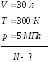Запишем
основное уравнение молекулярно-кинетической
теории:
,
где
-
концентрация молекул;
-
постоянная
Больцмана.
Следовательно:
;
;
.
Ответ:
.
10. Баллон емкостью
заполнен азотом, температура которого
.
Когда часть азота израсходовали, давление
в баллоне понизилось на
.
Определите массу
израсходованного азота. Процесс считать
изотермическим.
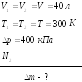Дано:
Решение:
Применим
уравнение Менделеева-Клапейрона:
,где
-
молярная масса азота. Для первого случая:
;
;
;
;
;
;
.
Ответ:
.
11. Масса
двухатомного газа находится под давлением
и имеет плотность
.
Найдите энергию теплового движения w
молекул газа при этих условиях.
Д
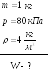ано:
Решение:
Энергия
теплового движения двухатомного газа
равна:
,
где
- число степеней
свободы молекулы двухатомного газа
(три
вращательные и две поступательные). Согласно уравнению Менделеева-
Клапейрона:
.
Тогда:
;
;
.
Ответ:
.
12. При изохорическом
нагревании кислорода объемом
давление газа изменилось на
.
Найдите количество теплоты
,
сообщенное газу.
Дано:
Решение:
При
изохорном процессе, количество теплоты,
сообщённое газу идёт на
изменение
его внутренней энергии:
;
.
Изменение внутренней
энергии
газа равно:
,
где
-
молярная теплоёмкость
газа
при постоянном объёме,
- число степеней свободы молекулы
кислорода (три вращательные и две поступательные для двухатомного
газа).
Следовательно:
(1).
Согласно уравнению
Менделеева-Клапейрона:
;
;
;
;
;
(2).
Подставляем (2)
в (1):
.
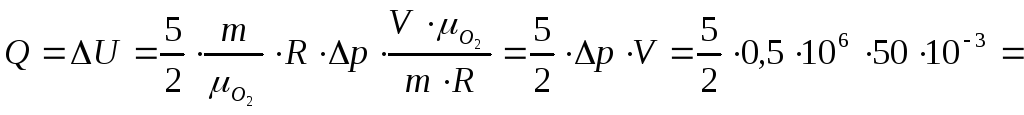
Ответ:
.