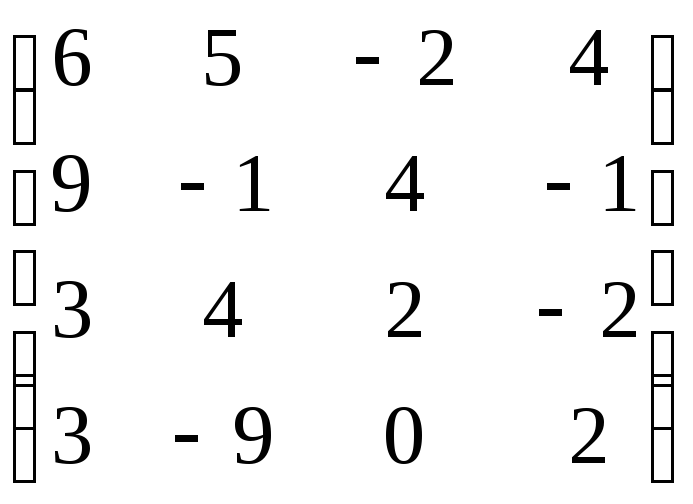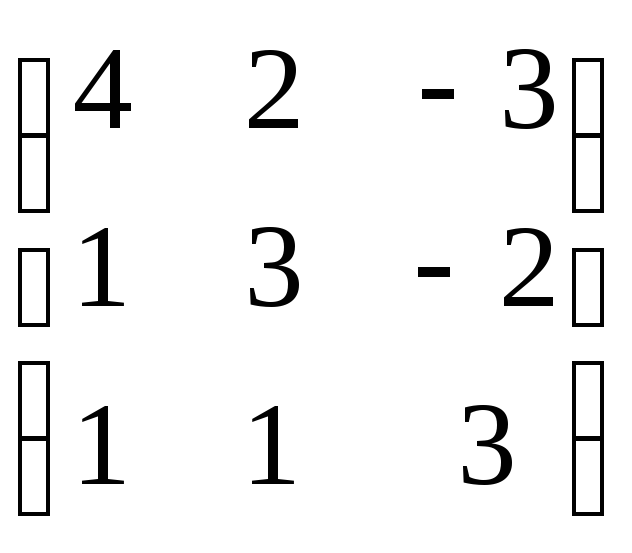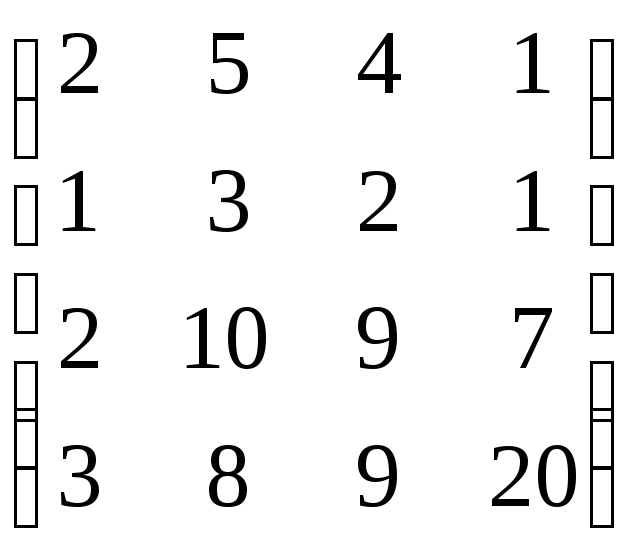Линейная алгебра, ПНИПУ
.docК о н т р о л ь н а я р а б о т а № 1
Линейная алгебра и аналитическая геометрия
Задание 1. Вычислить выражение А2+2АВ5ВТАТ.
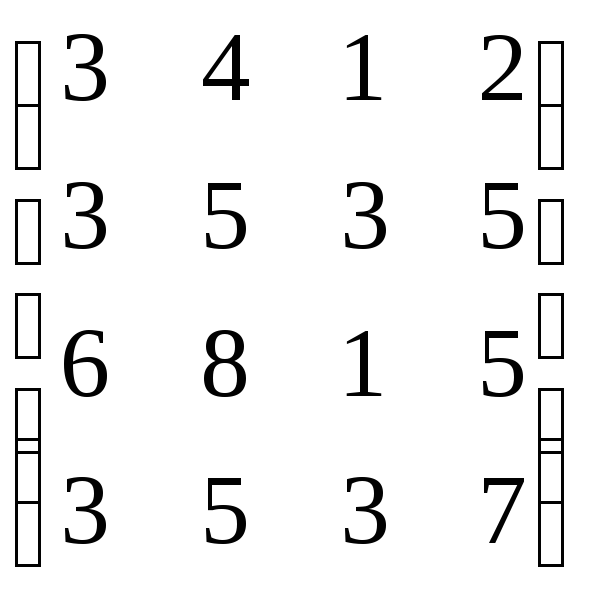
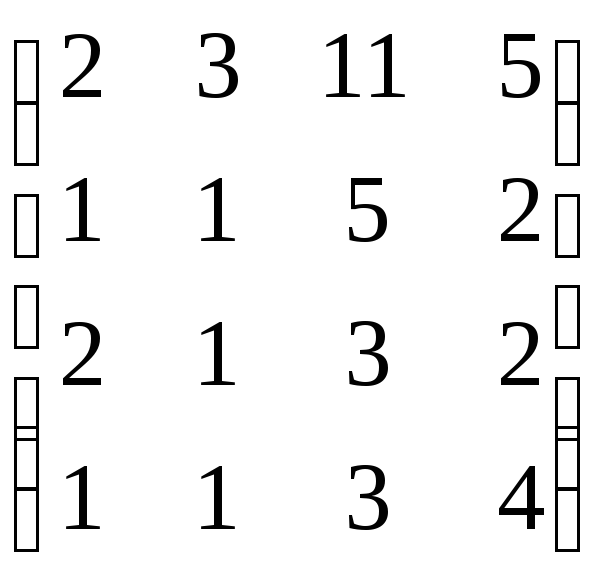
Задание 2. Найти ранг матрицы:
а) методом окаймления миноров;
б) с помощью элементарных преобразований.
Задание 3. Решить матричное уравнение.
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
|
Задание 1 |
Задание 1 |
Задание 1 |
Задание 1 |
|
А=
|
А= |
А= |
А= |
|
Задание 2 |
Задание 2 |
Задание 2 |
Задание 2 |
|
а)
б)
|
а)
б)
|
а)
б)
|
а)
б)
|
|
Задание 3
|
Задание 3
|
Задание 3
|
Задание 3
|
|
Вариант 5 |
Вариант 6 |
Вариант 7 |
Вариант 8 |
|
Задание 1 |
Задание 1 |
Задание 1 |
Задание 1 |
|
А= |
А= |
А= |
А= |
|
Задание 2 |
Задание 2 |
Задание 2 |
Задание 2 |
|
а)
б)
|
а)
б)
|
а)
б)
|
а)
б)
|
|
|
|
|
|
|
Задание 3
|
Задание 3
|
Задание 3
|
Задание 3
|
|
Вариант 9 |
Вариант 10 |
Вариант 11 |
Вариант 12 |
|
Задание 1 |
Задание 1 |
Задание 1 |
Задание 1 |
|
А= |
А= |
А= |
А= |
|
Задание 2 |
Задание 2 |
Задание 2 |
Задание 2 |
|
а)
б)
|
а)
б)
|
а)
б)
|
а)
б)
|
|
Задание 3
|
Задание 3
|
Задание 3
|
Задание 3
|
|
Вариант 13 |
Вариант 14 |
Вариант 15 |
Вариант 16 |
|
Задание 1 |
Задание 1 |
Задание 1 |
Задание 1 |
|
А= |
А= |
А= |
А= |
|
Задание 2 |
Задание 2 |
Задание 2 |
Задание 2 |
|
а)
б)
|
а)
б)
|
а)
б)
|
а)
б)
|
|
Задание 3
|
Задание 3
|
Задание 3
|
Задание 3
|
|
Вариант 17 |
Вариант 18 |
Вариант 19 |
Вариант 20 |
|
Задание 1 |
Задание 1 |
Задание 1 |
Задание 1 |
|
А=
В= |
А=
В= |
А=
В= |
А=
В= |
|
Задание 2 |
Задание 2 |
Задание 2 |
Задание 2 |
|
а)
б)
|
а)
б)
|
а)
б)
|
а)
б)
|
|
Задание 3
|
Задание 3
|
Задание 3
|
Задание 3
|
|
Вариант 21 |
Вариант 22 |
Вариант 23 |
Вариант 24 |
|
Задание 1 |
Задание 1 |
Задание 1 |
Задание 1 |
|
А=
В= |
А= |
А= |
А= |
|
Задание 2 |
Задание 2 |
Задание 2 |
Задание 2 |
|
а)
б)
|
а)
б)
|
а)
б)
|
а)
б)
|
|
Задание 3
|
Задание 3
|
Задание 3
|
Задание 3
|
|
Вариант 25 |
Вариант 26 |
Вариант 27 |
Вариант 28 |
|
Задание 1 |
Задание 1 |
Задание 1 |
Задание 1 |
|
А=
|
А=
В= |
А= |
А=
|
|
Задание 2 |
Задание 2 |
Задание 2 |
Задание 2 |
|
а)
б)
|
а)
б)
|
а)
б)
|
а)
б)
|
|
Задание 3
|
Задание 3
|
Задание 3
|
Задание 3
|
|
Вариант 29 |
Вариант 30 |
|
|
|
|
Задание 1 |
Задание 1 |
|
|
|
|
А=
В= |
А=
В= |
|
|
|
|
Задание 2 |
Задание 2 |
|
|
|
|
а)
б)
|
а)
б)
|
|
|
|
|
Задание 3
|
Задание 3
|
|
||
Задание 4
Проверить совместность системы уравнений и в случае совместности решить ее:
а) по формулам Крамера;
б) с помощью обратной матрицы (матричным методом);
в) методом Гаусса.
-
1.
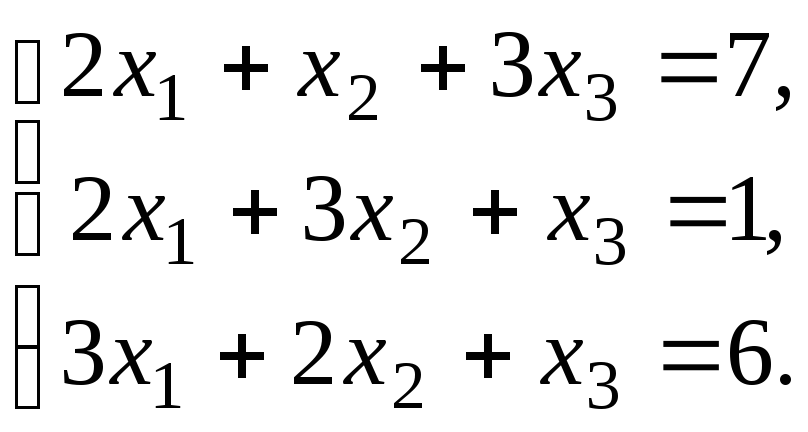
2.
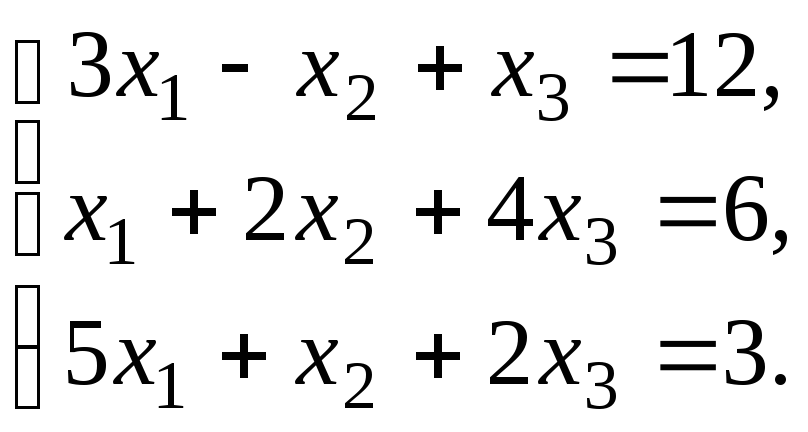
3.
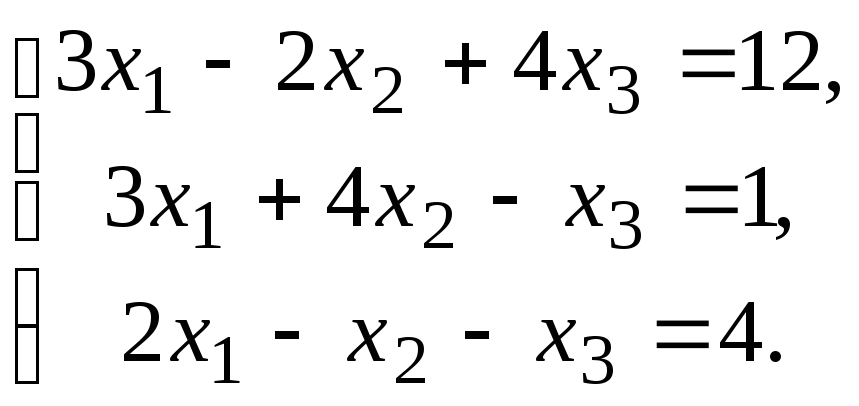
4.
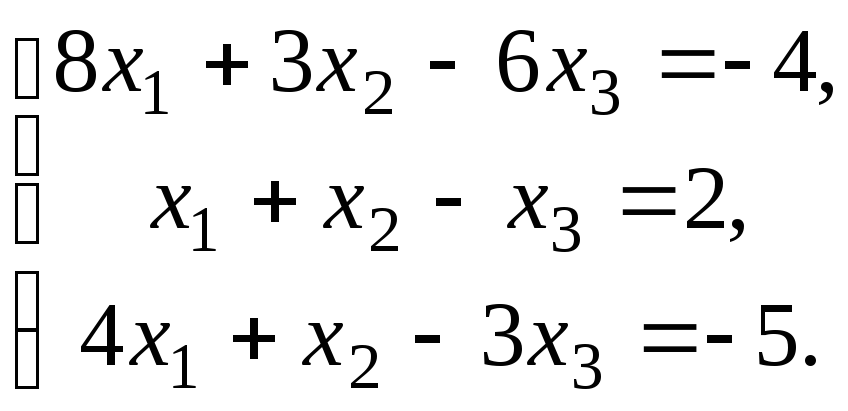
5.
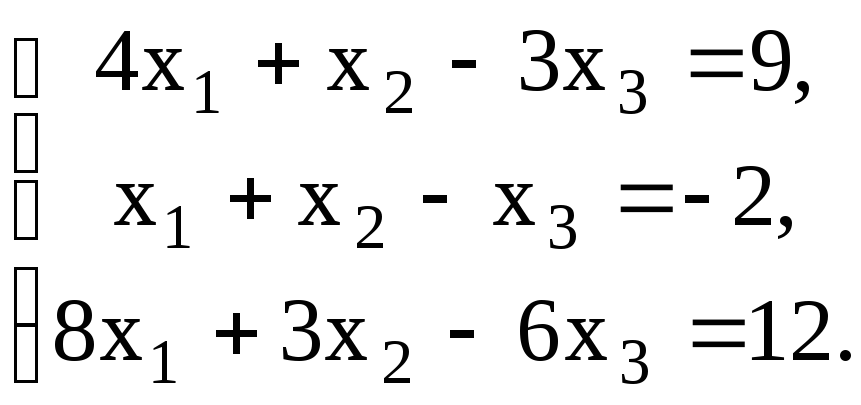
6.
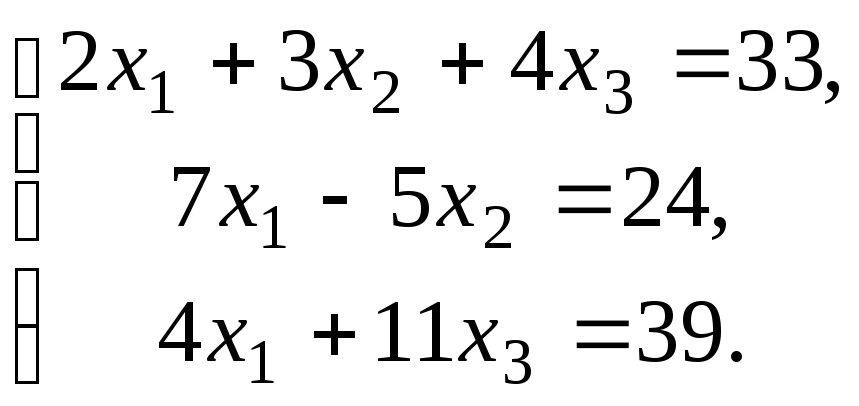
7.
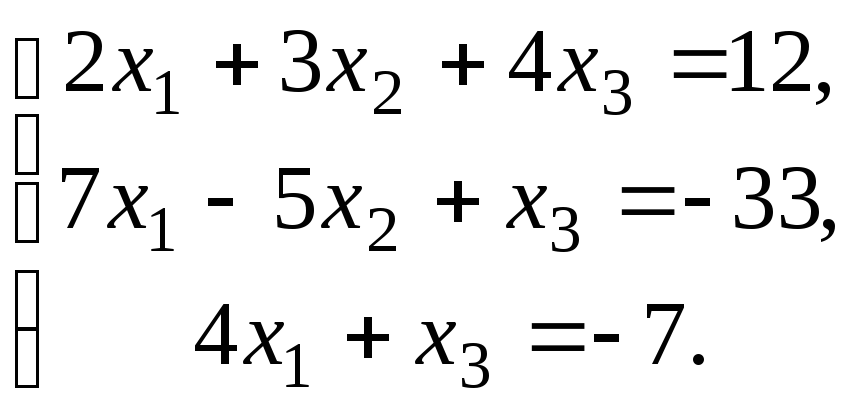
8.
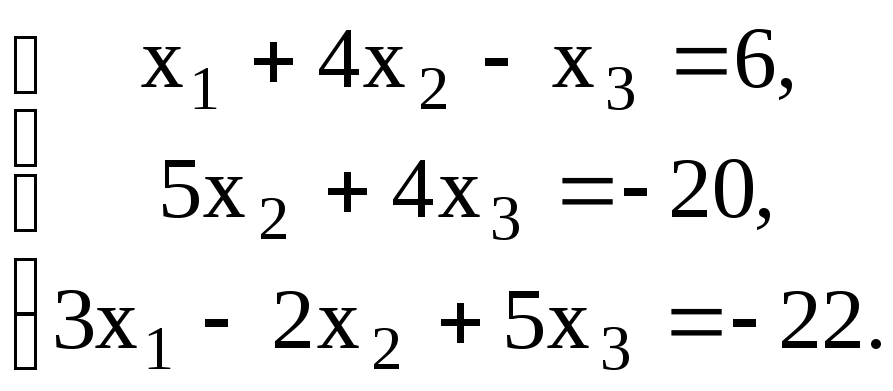
9.
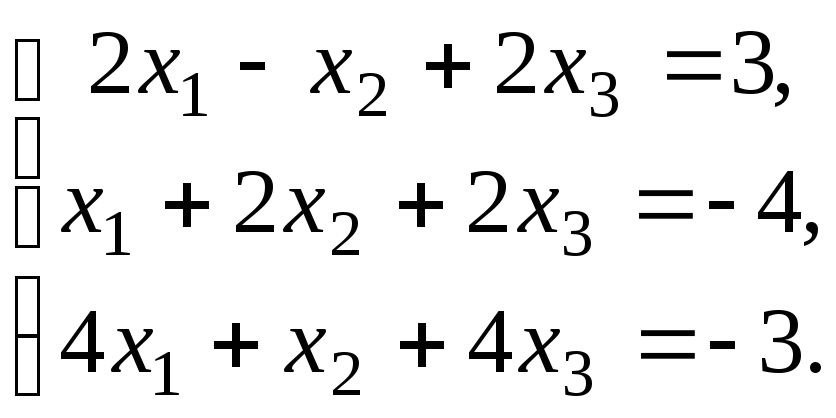
10.
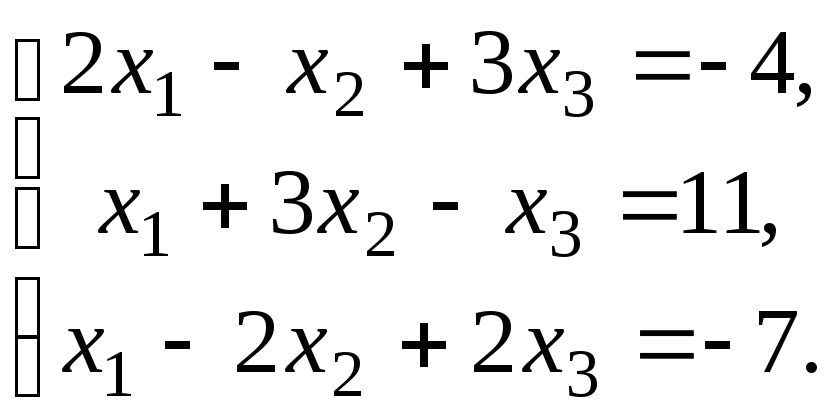
-
11.
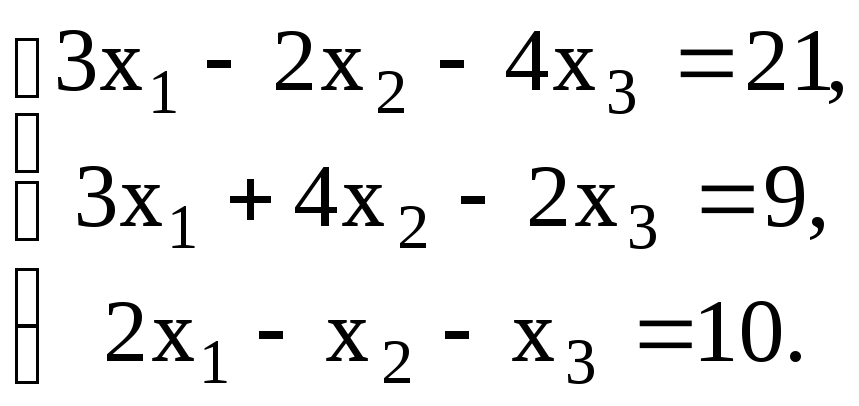
12.
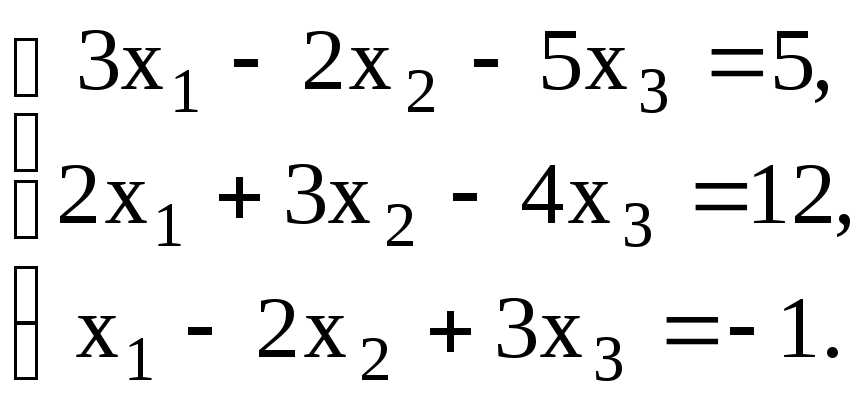
13.
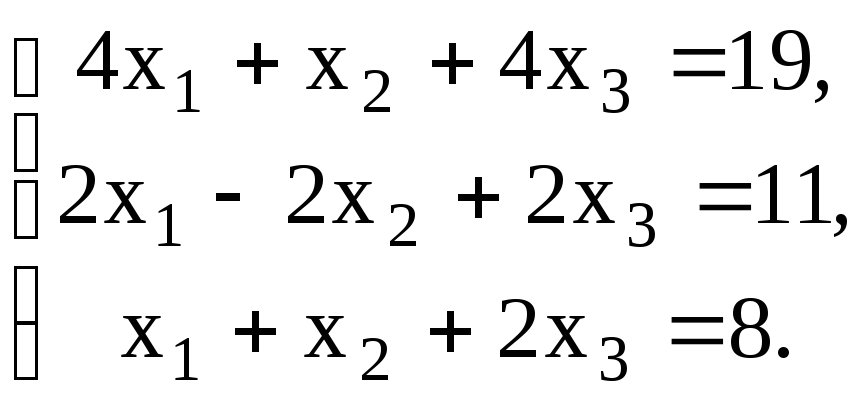
14.
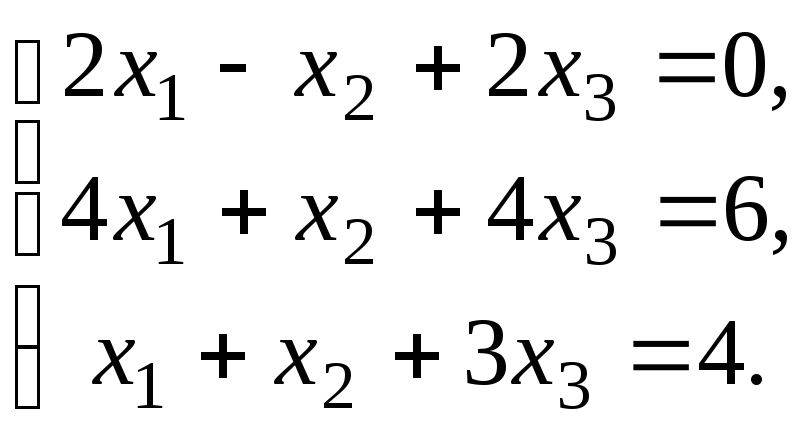
15.
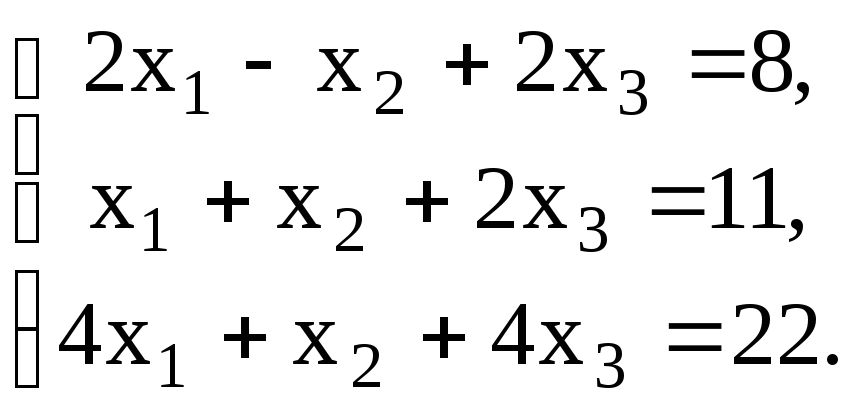
16.
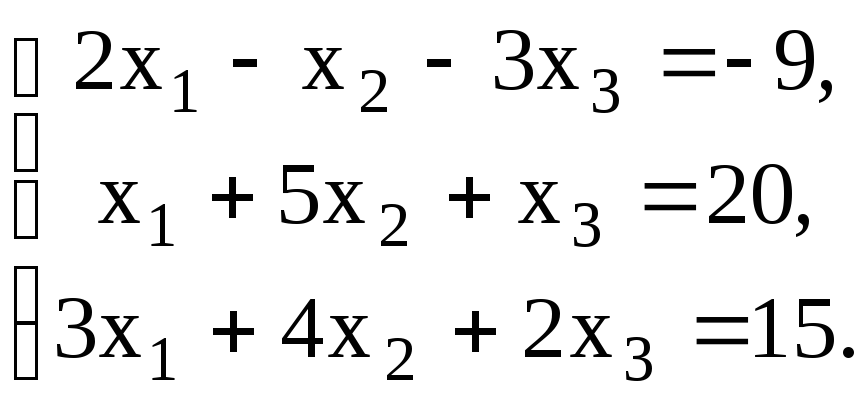
17.
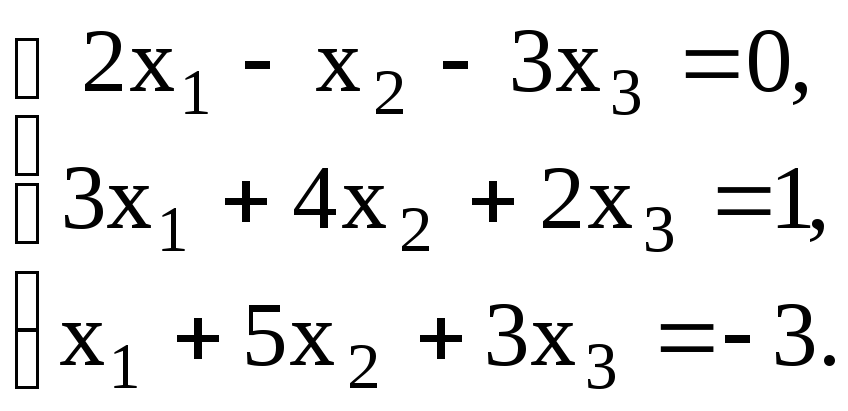
18.
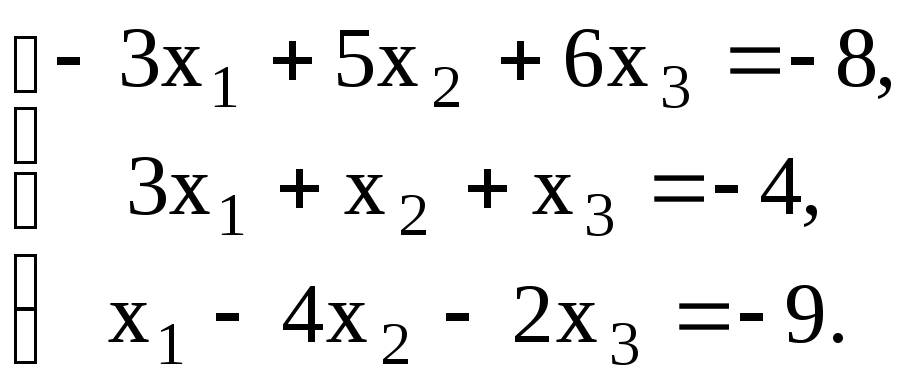
19.
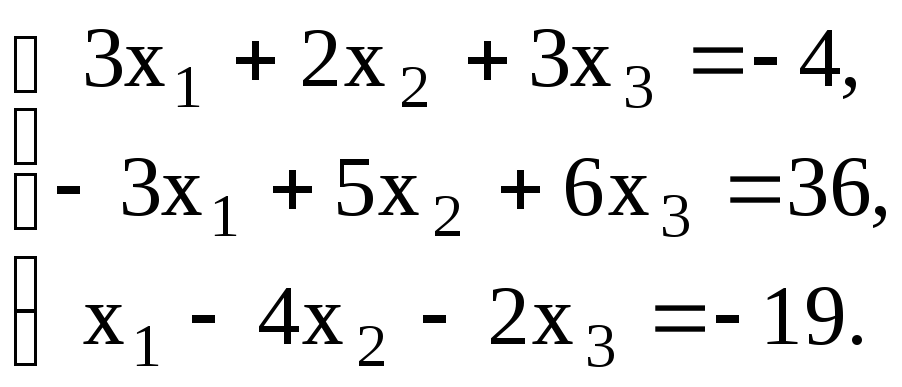
20.
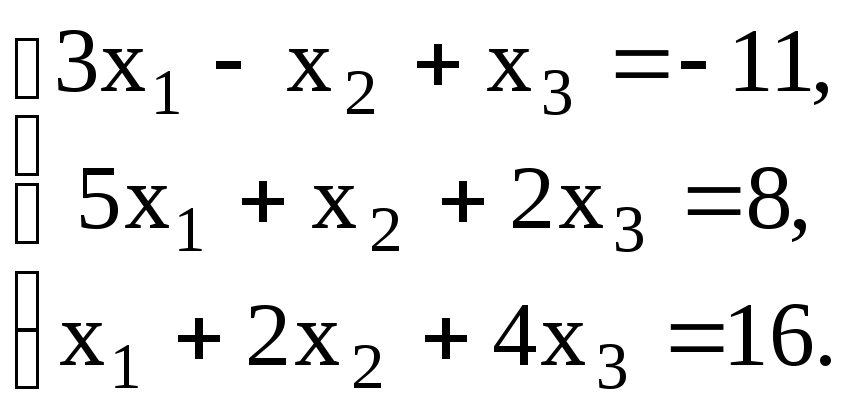
21.
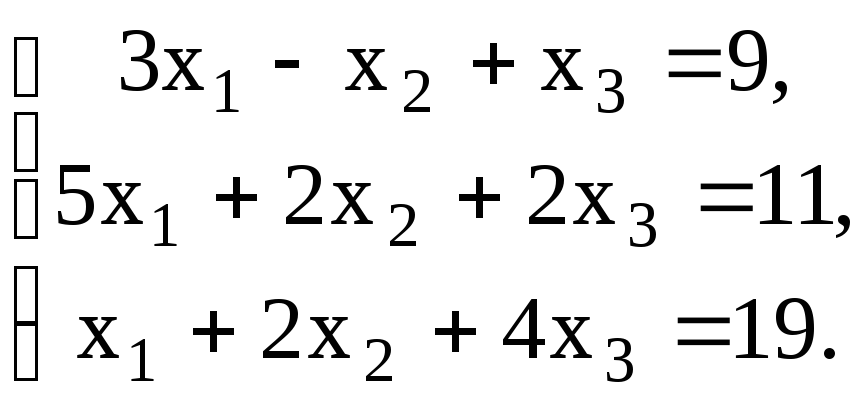
22.
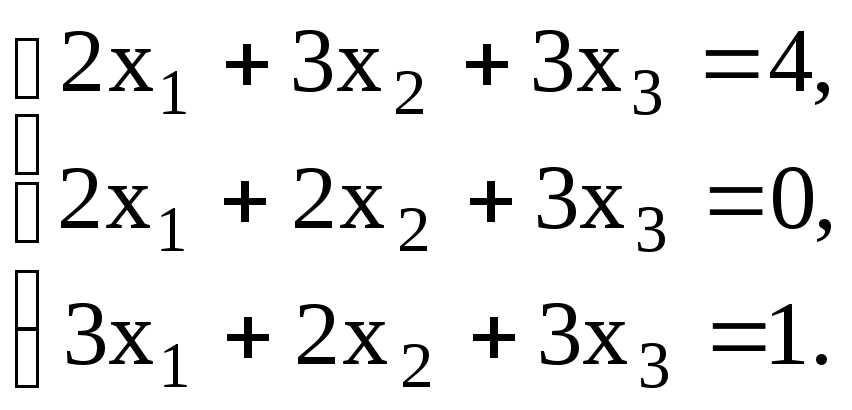
23.
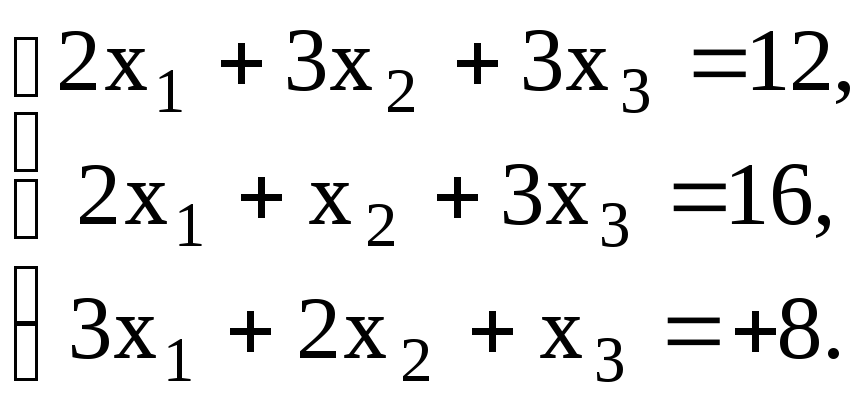
24.
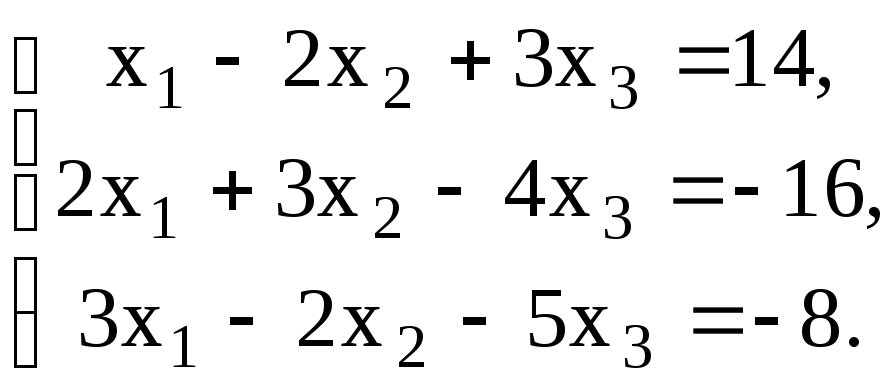

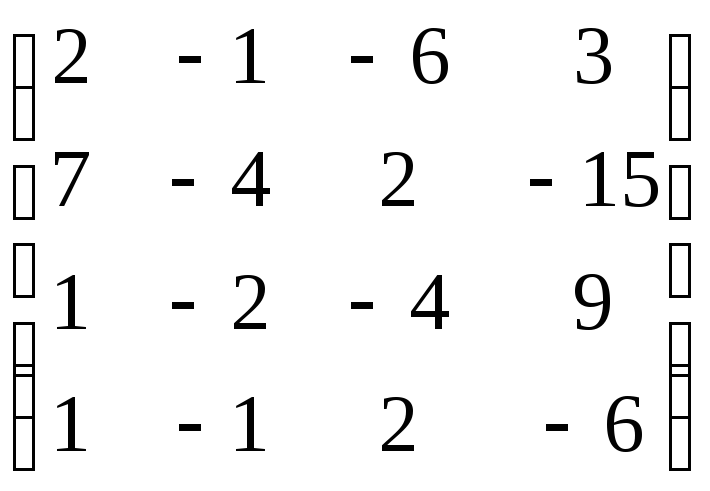 ,
В=
,
В=
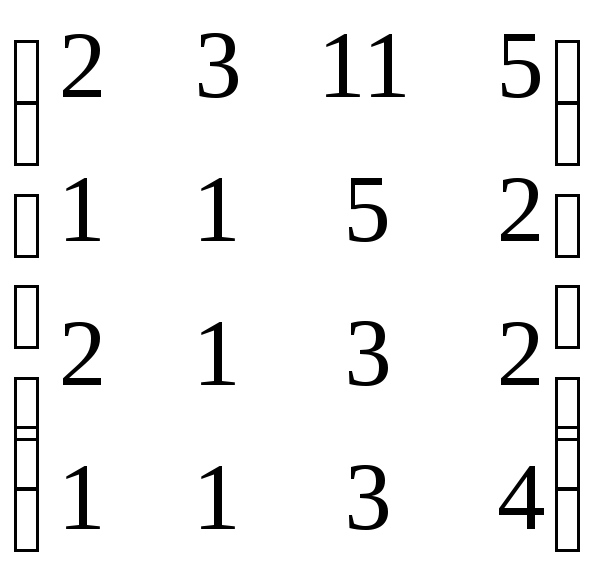 ,
В=
,
В=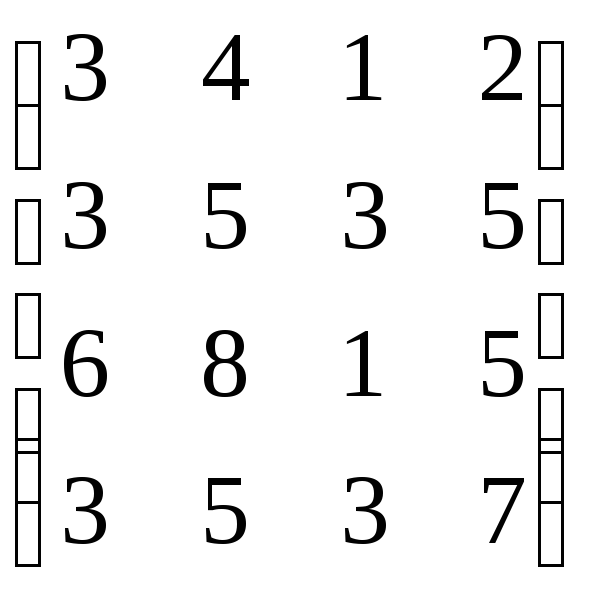
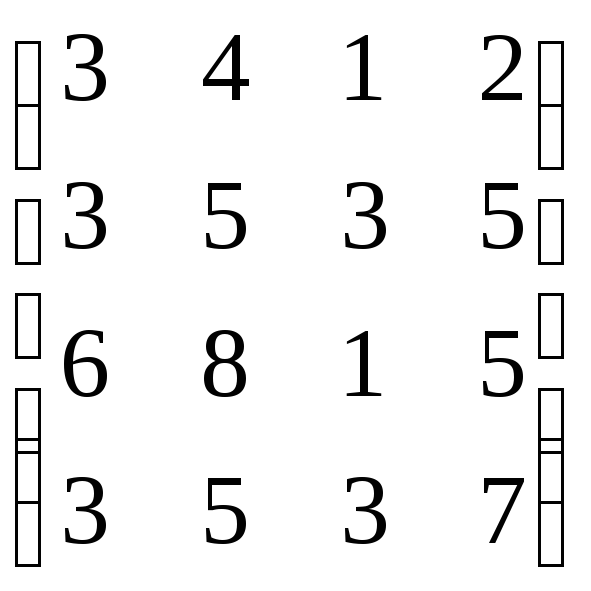 ,
В=
,
В=
 ,
В=
,
В=
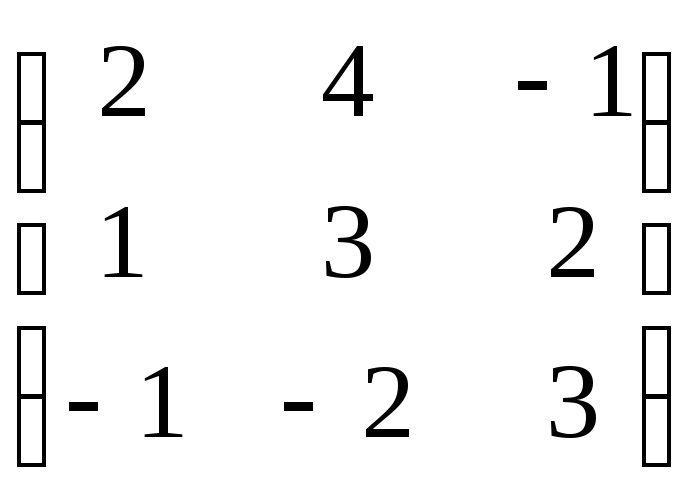
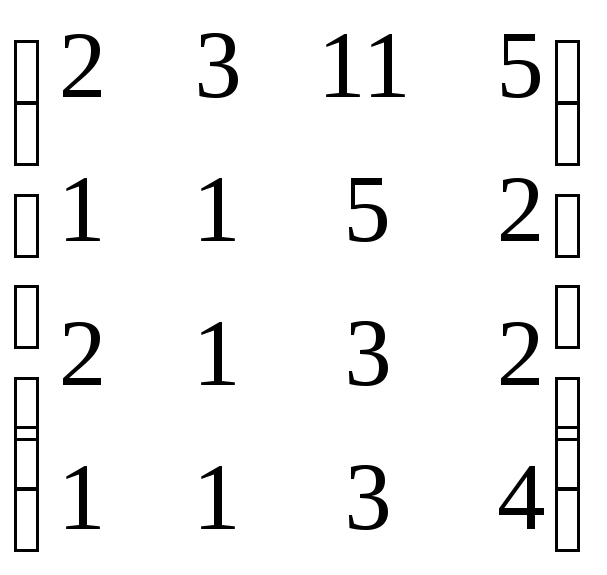
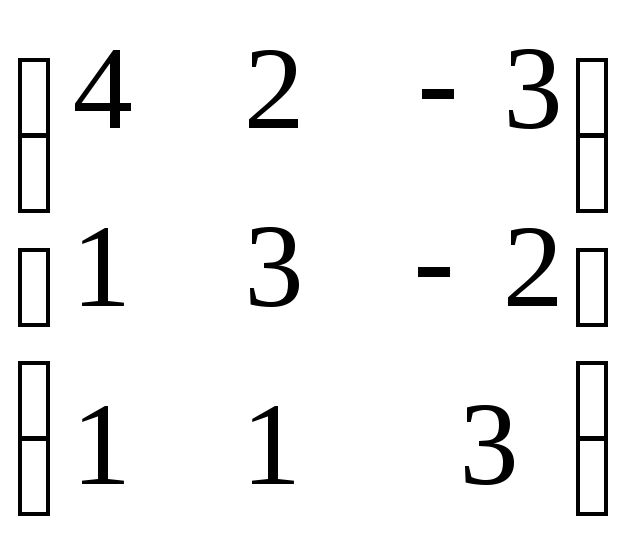
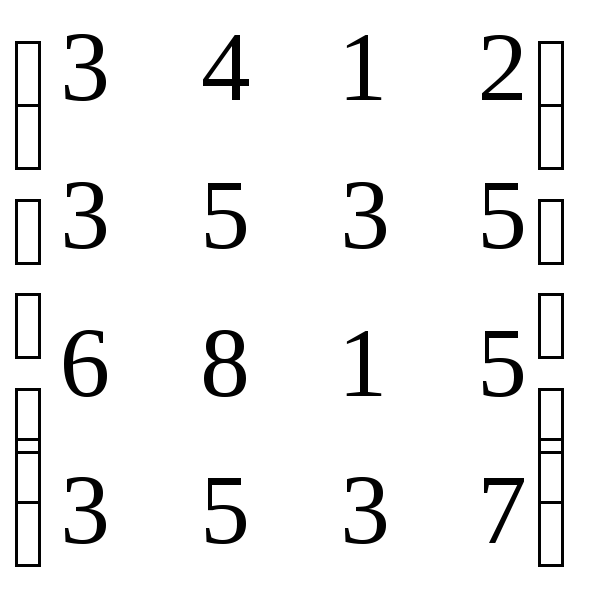




 ,
В=
,
В=
 ,
В=
,
В=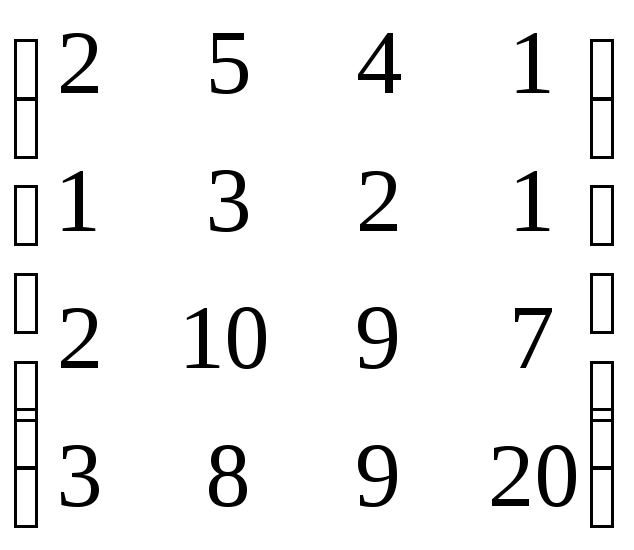
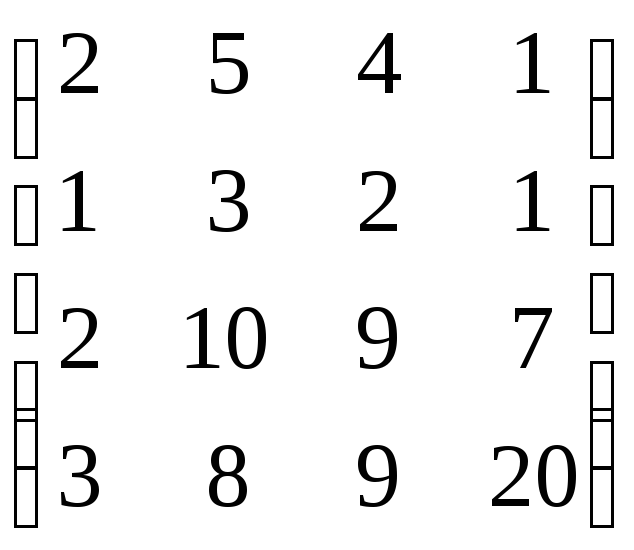 ,
В=
,
В=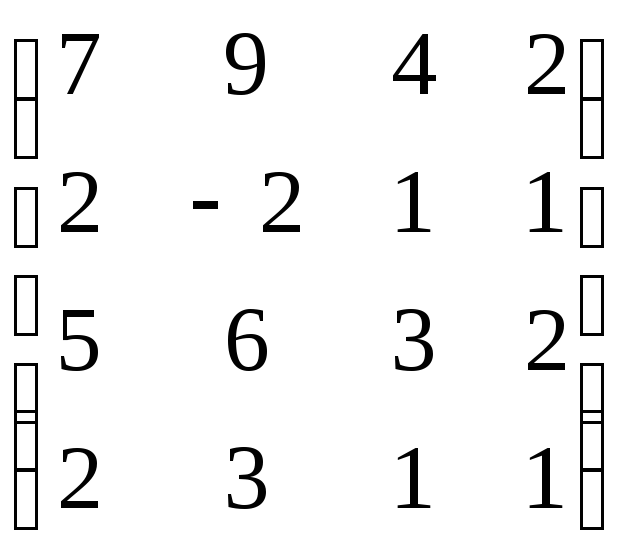
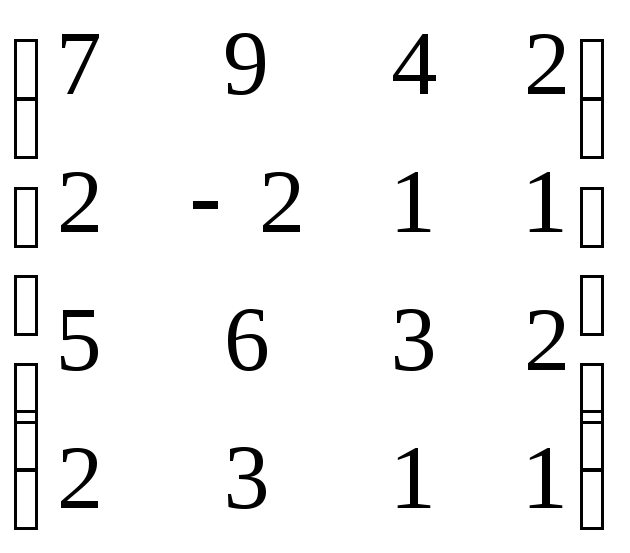 ,
В=
,
В=

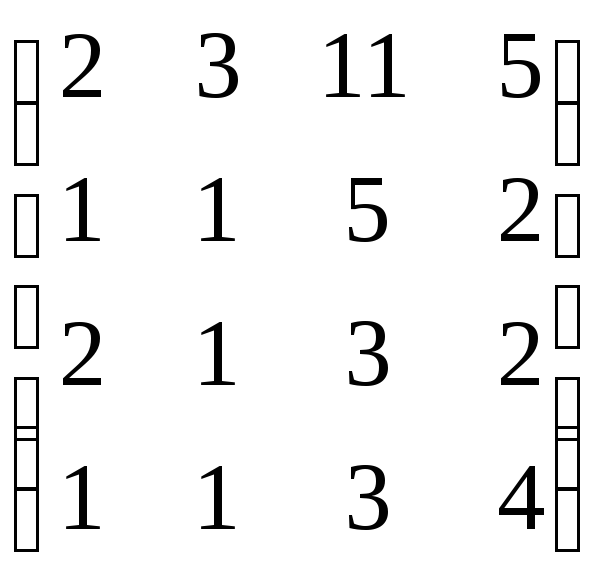

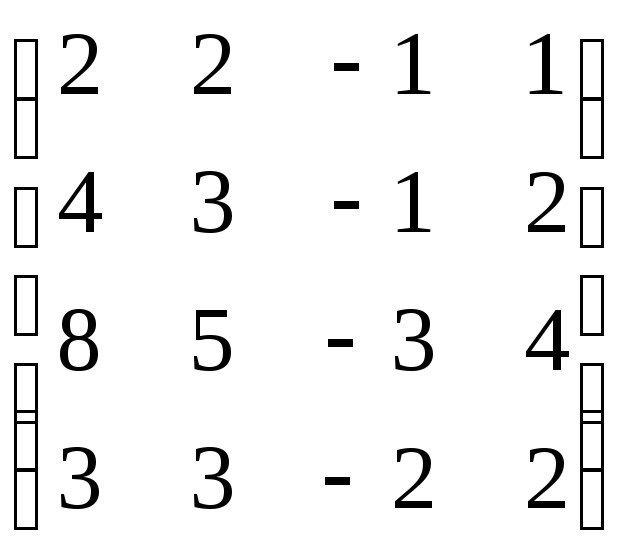




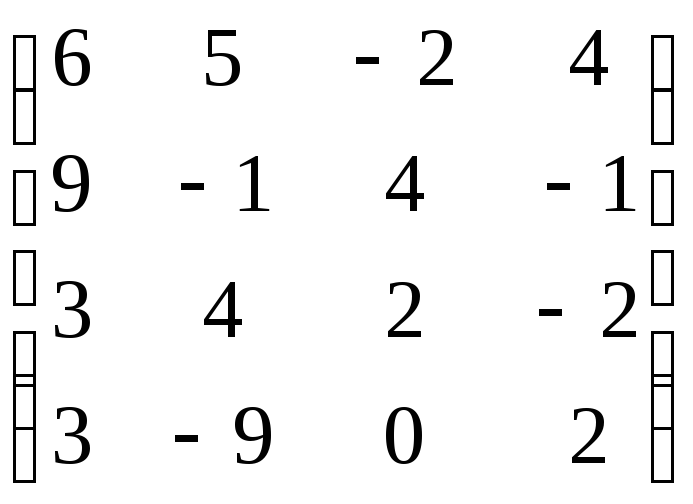 ,
В=
,
В=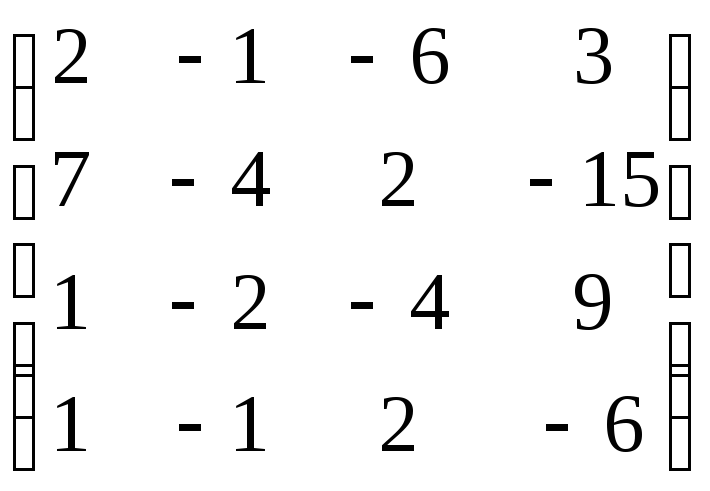
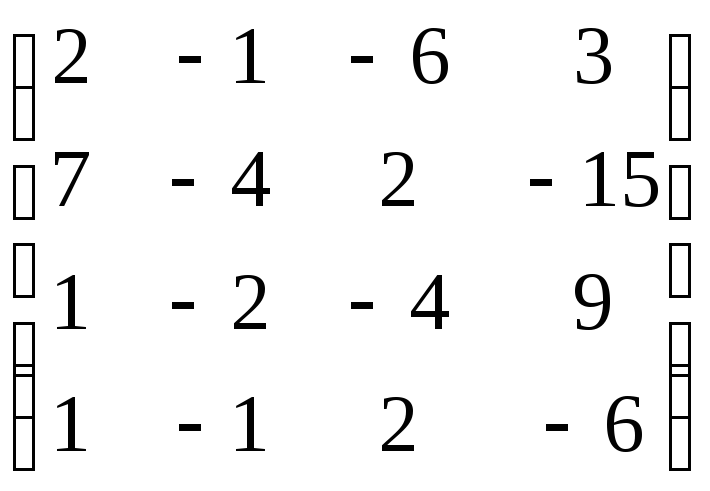 ,
В=
,
В=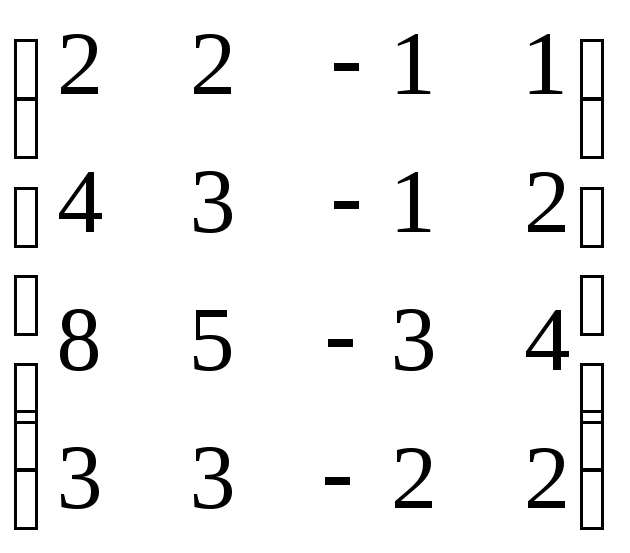
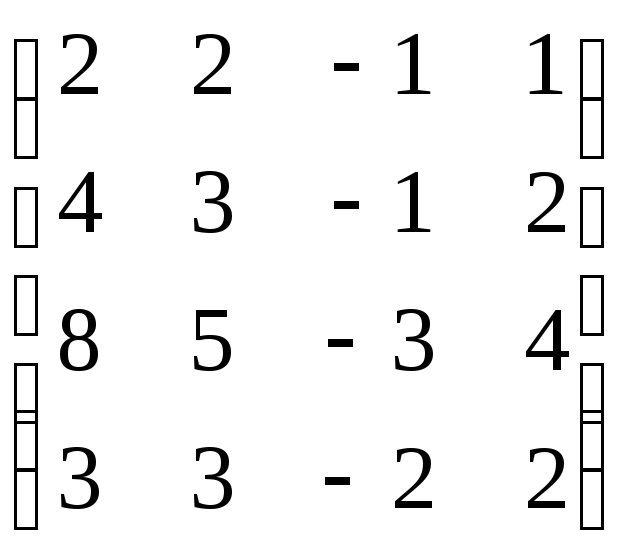 ,
В=
,
В=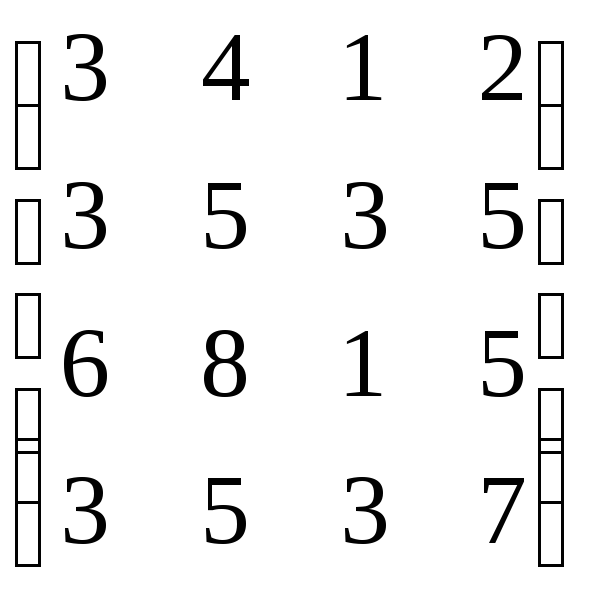
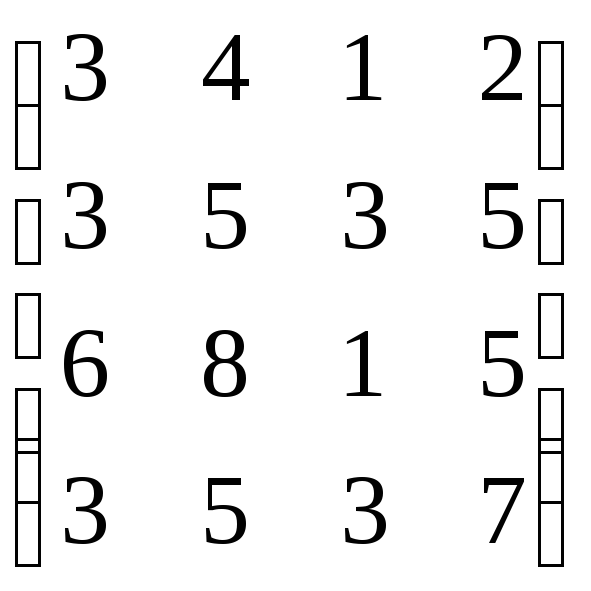 ,
В=
,
В=




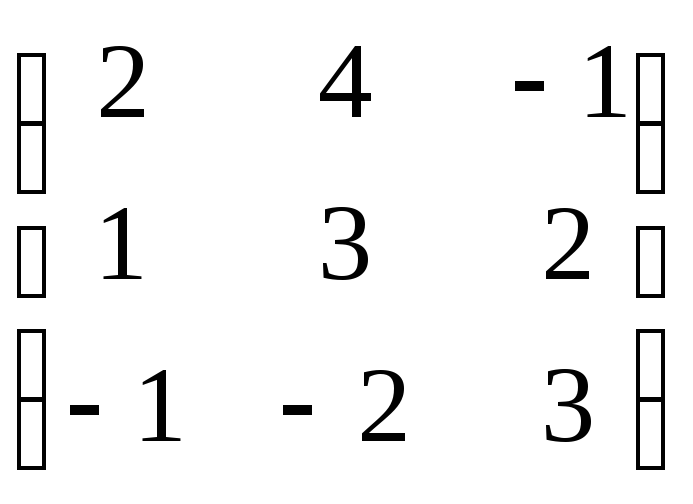


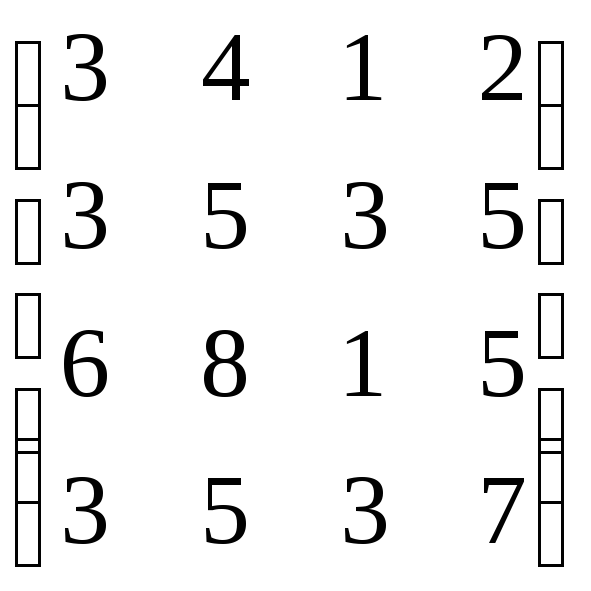
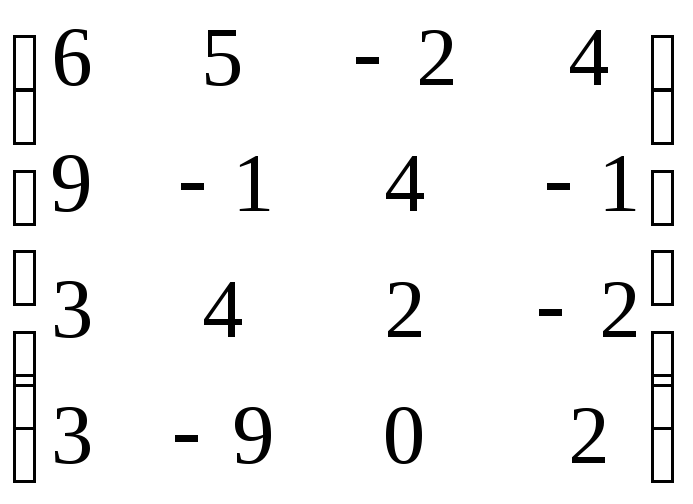 ,
В=
,
В=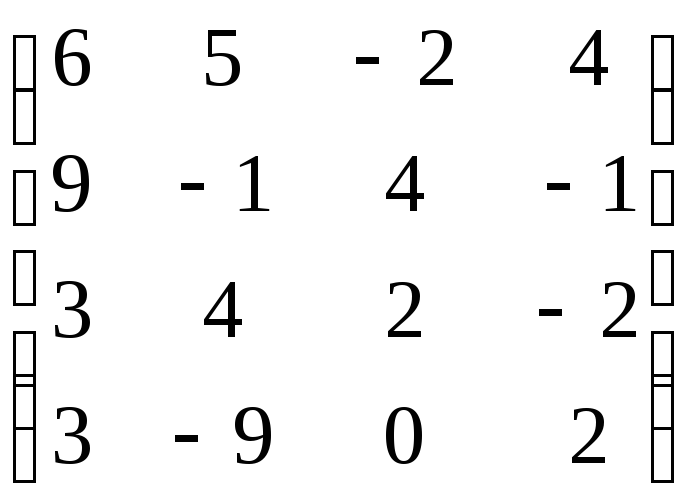
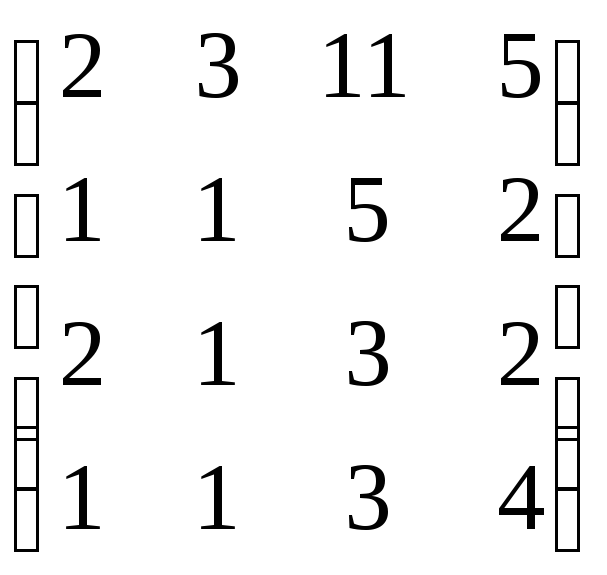 ,
В=
,
В=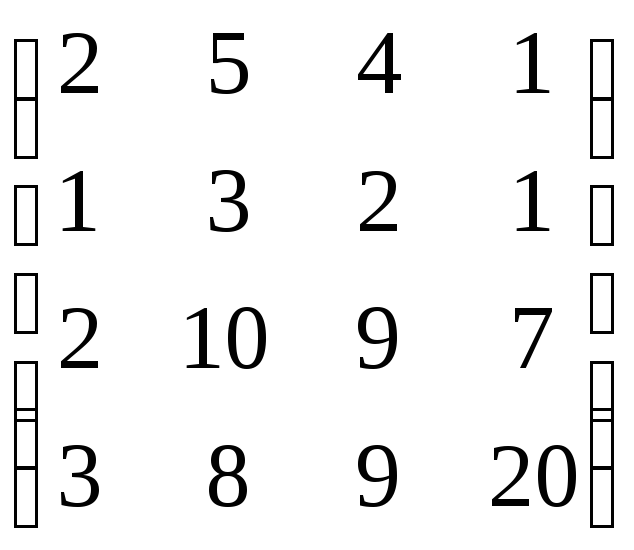
 ,
В=
,
В=
 ,
В=
,
В=

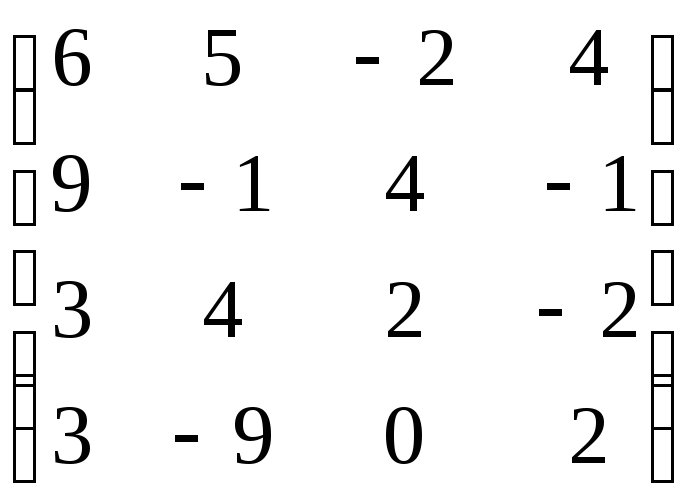
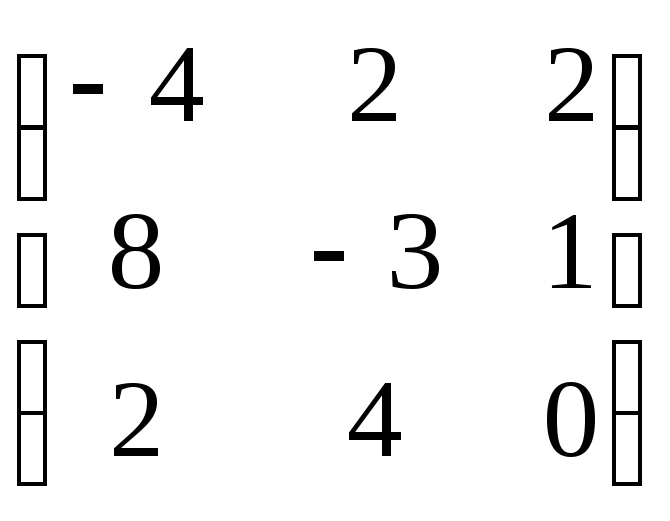
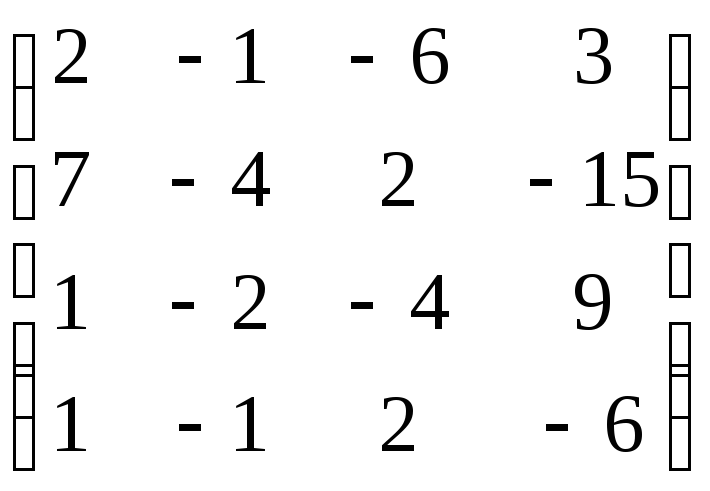
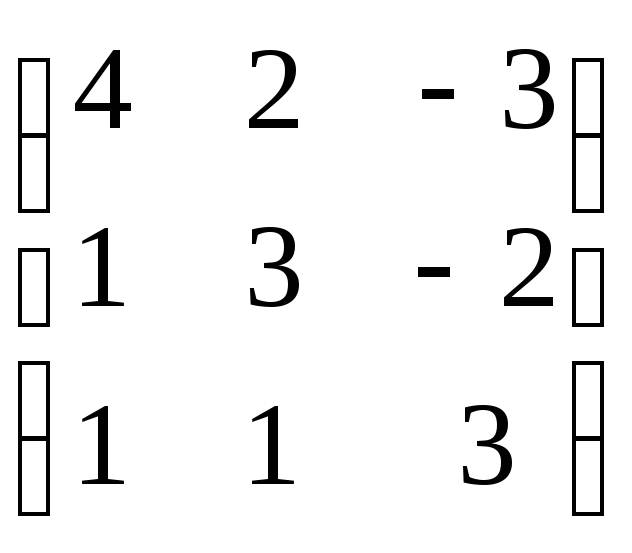


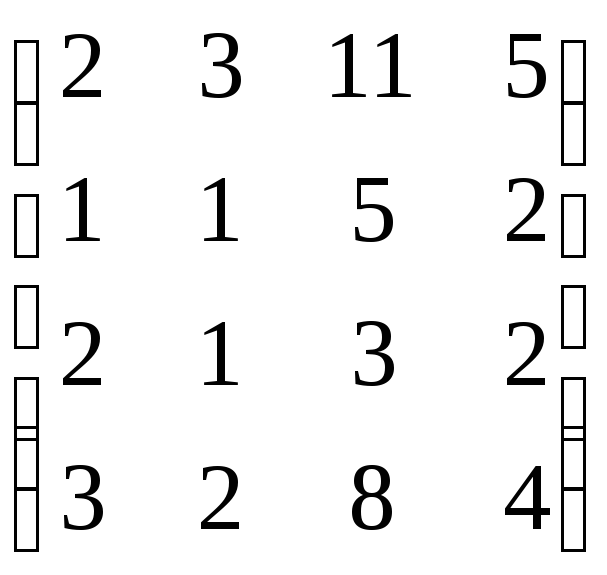
 ,
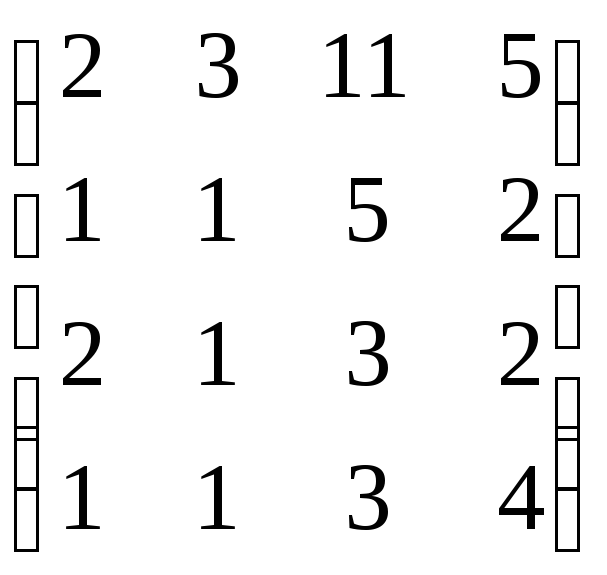
,
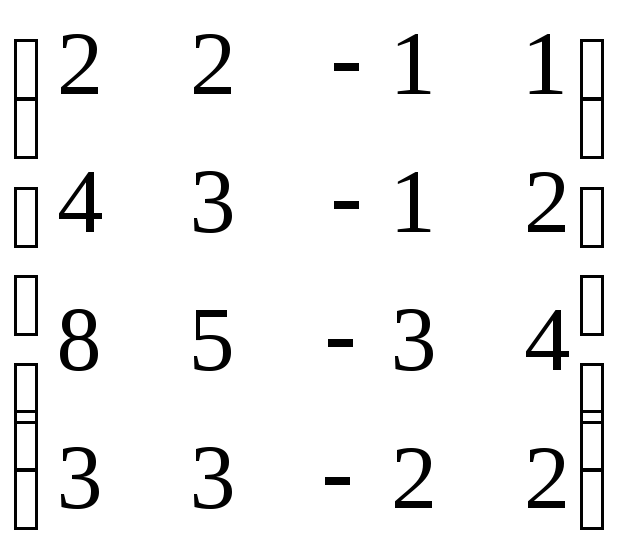 ,
,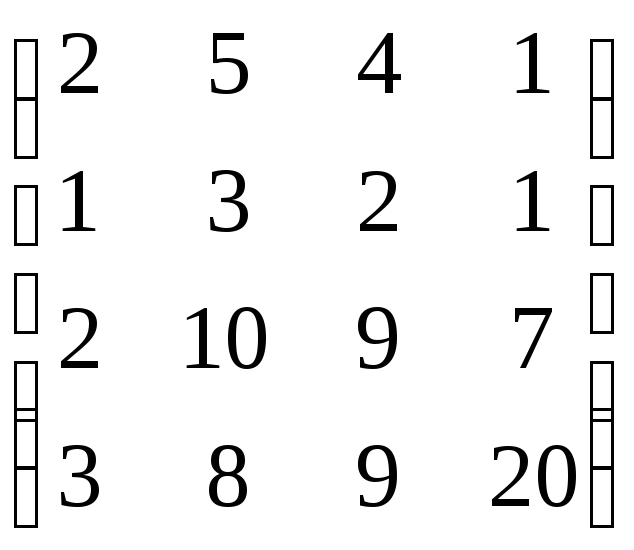
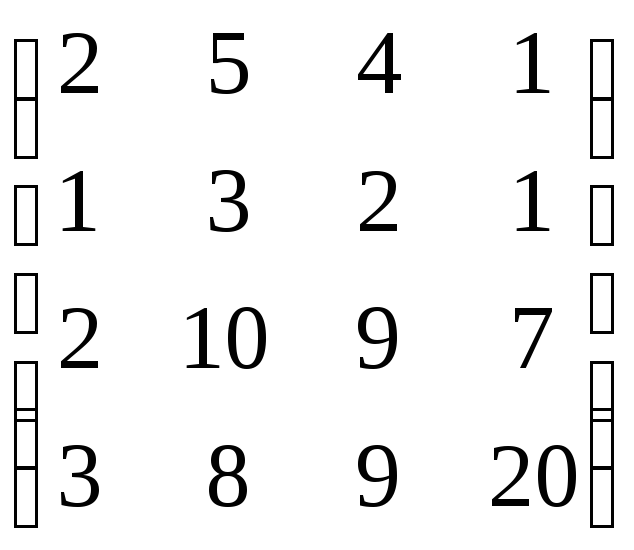 ,
,
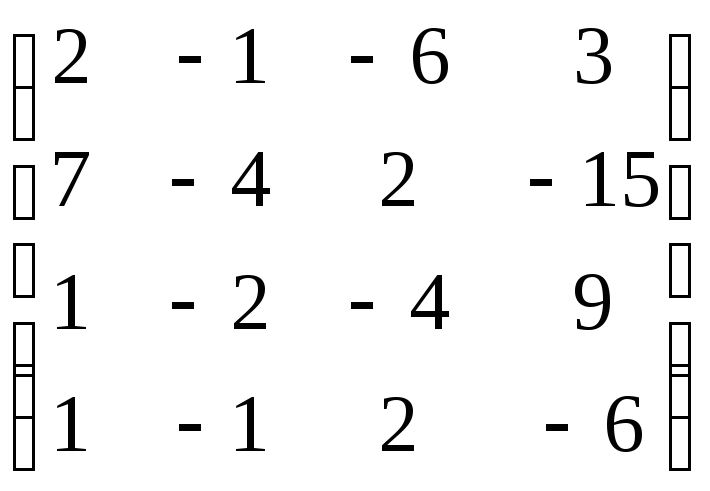 ,
,

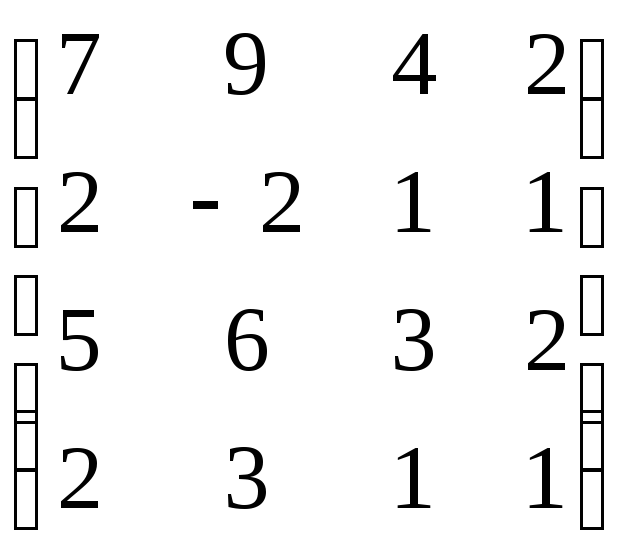
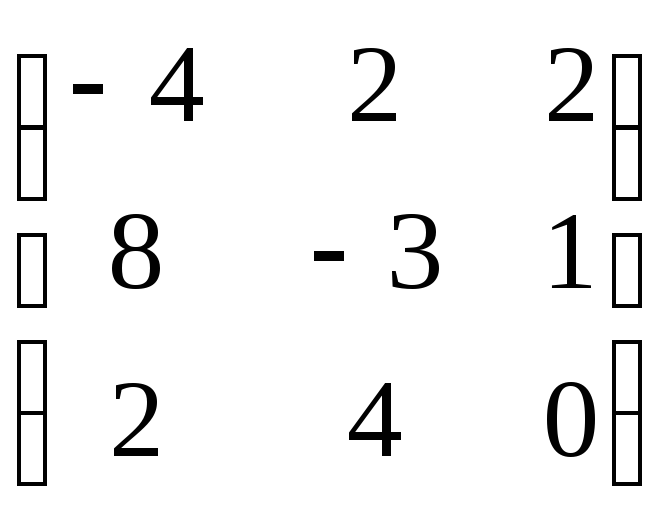
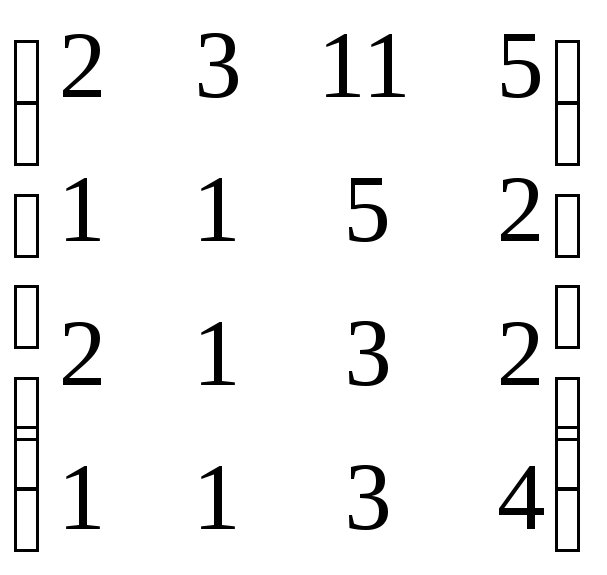



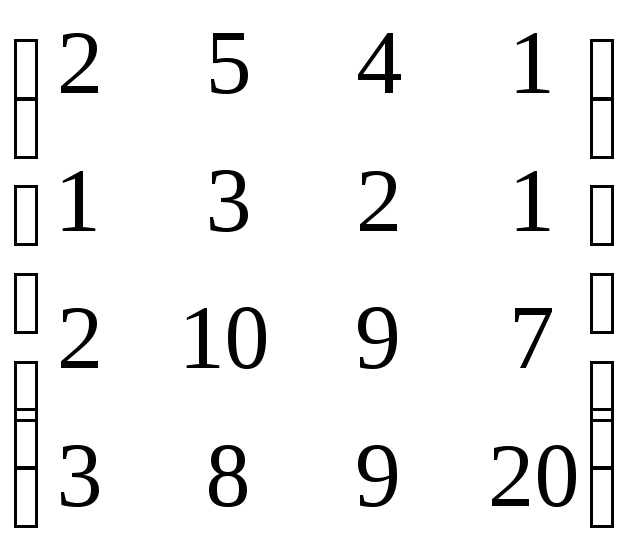
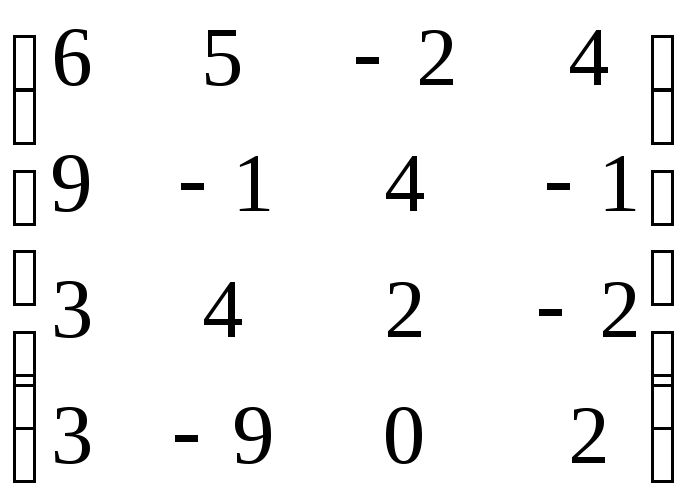 ,
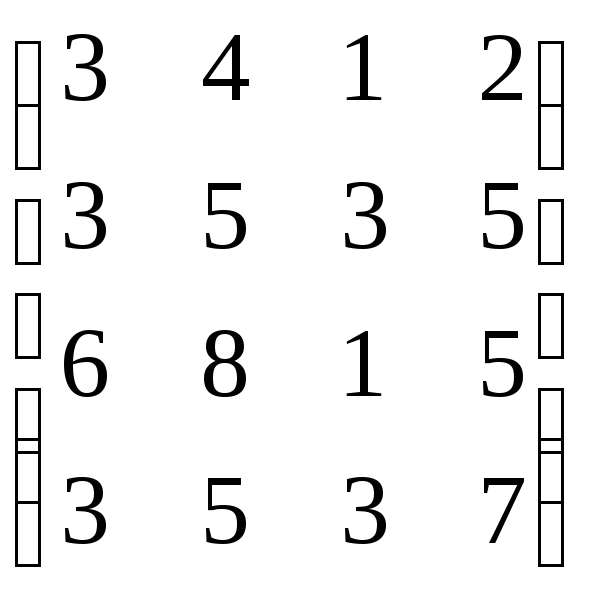
,
 ,
В=
,
В=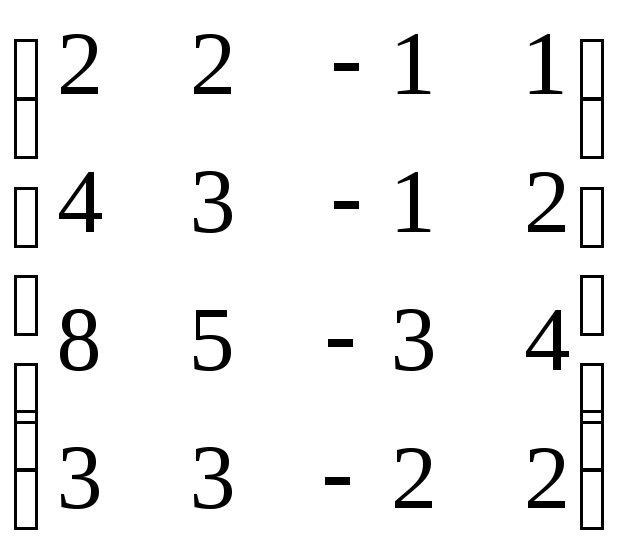
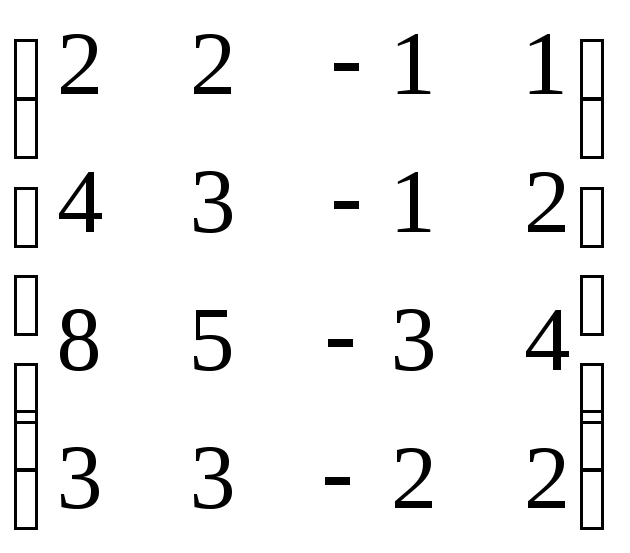 ,
В=
,
В=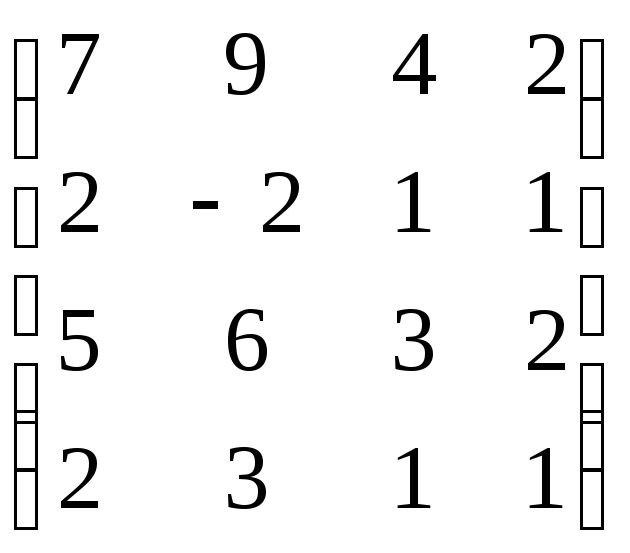
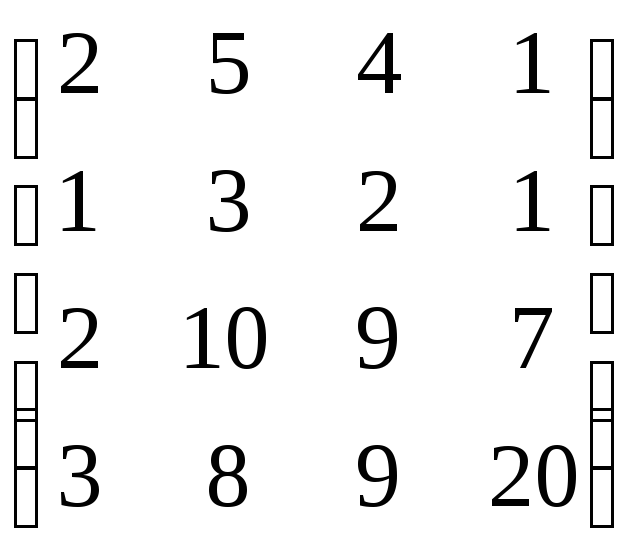 ,
В=
,
В=

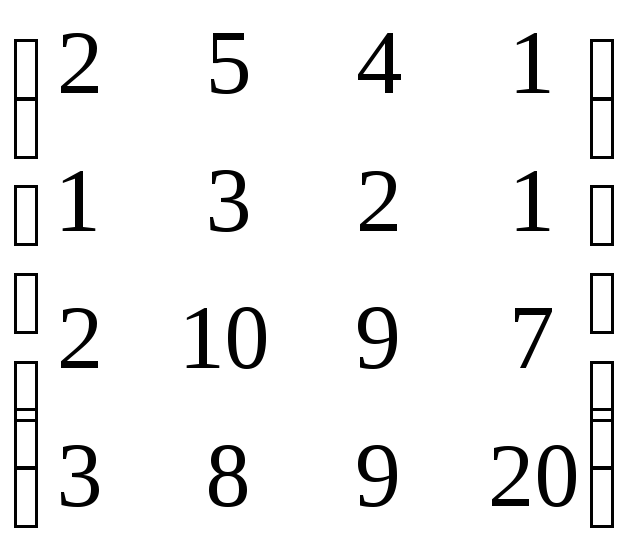



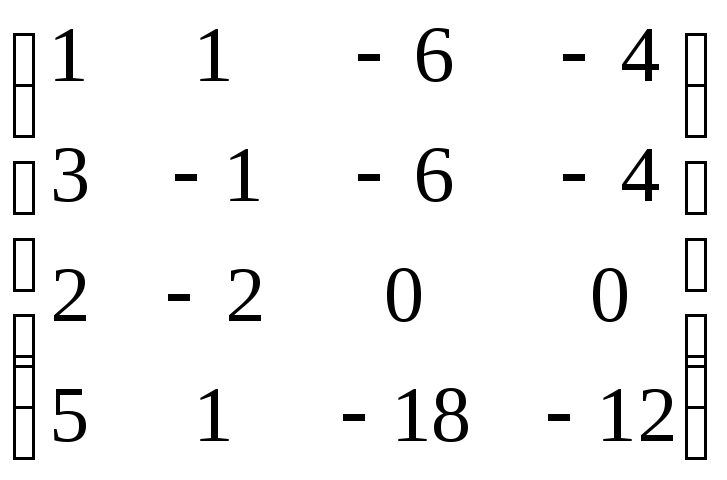
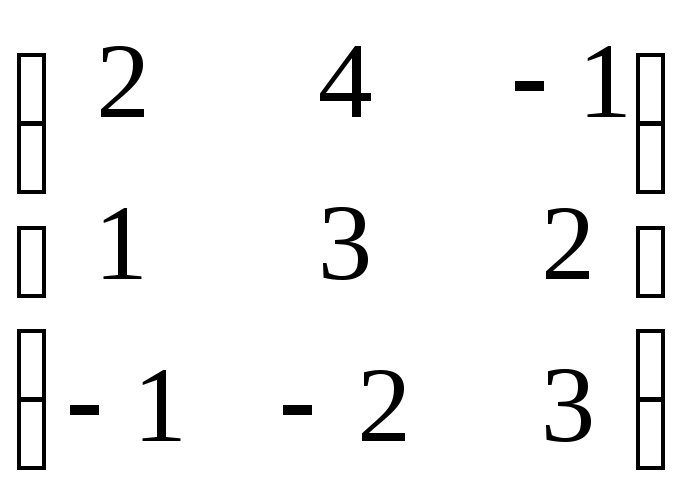

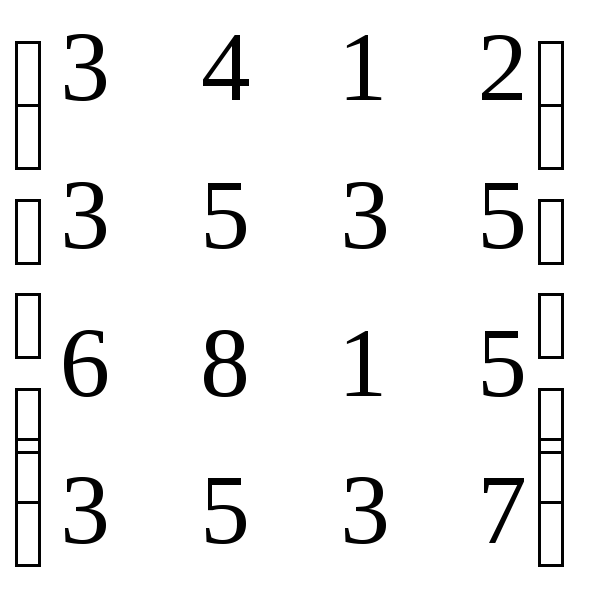 ,
В=
,
В=
 ,
,

 ,
В=
,
В=
 ,
В=
,
В=





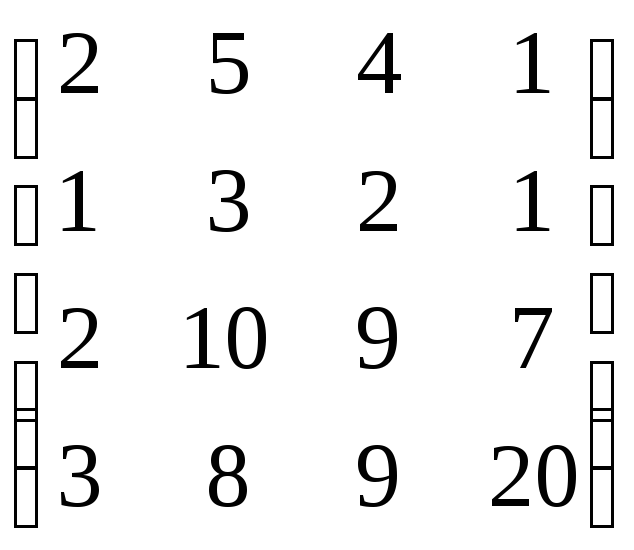

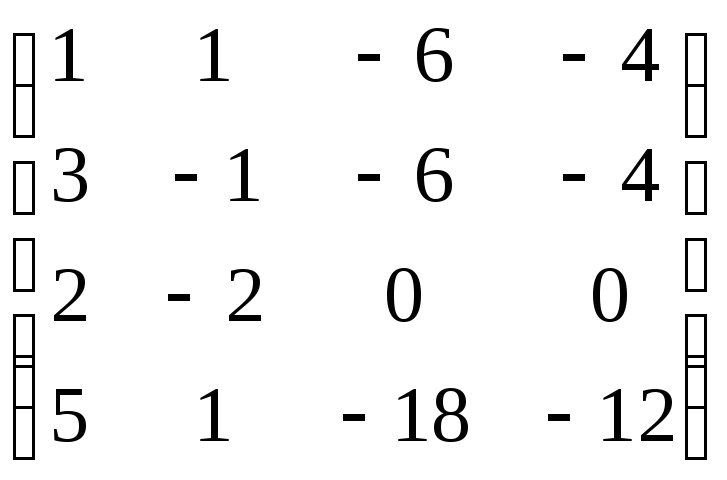
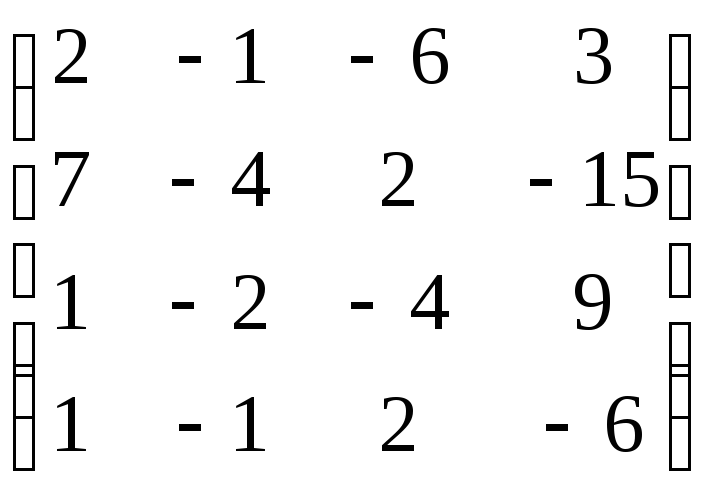 ,
,
 ,
,