
- •1.1.1 Рабочее тело
- •1.1.2 Состояние рабочего тела. Параметры состояния.
- •1.2. Газовые смеси Характеризуются законом Дальтона, который гласит:
- •1.3. Понятие о равновесном и обратимом процессах.
- •1.4. Теплоемкость газов.
- •1.5. Первый закон термодинамики.
- •1.5.1. Уравнение первого закона термодинамики.
- •1.6. Функции состояния и функции процесса.
- •1.7. Энтропия как параметр состояния идеального газа.
- •1.8. Работа газа при неравновесном процессе.
- •1.8. Исследование газовых процессов.
- •Политропные процессы
- •I Закон термодинамики для потока газа .
- •II-й закон термодинамики.
- •Круговые процессы (циклы).
- •Цикл Карно.
- •Т1 и т2 - температуры горячего и холодного источников тепла
- •Эквивалентный цикл Карно
- •Пример:
1.8. Исследование газовых процессов.
Изохорный, изобарный, изотермический, адиабатный, политропный.
В каждом процессе один из параметров состояния постоянный (const).
Изохорный процесс:
![]() ;
;
![]() Уравнение состояния идеального газа
для 1 и 2 го состояний:
Уравнение состояния идеального газа
для 1 и 2 го состояний:
Рис. Изохора
![]()
![]() поделим
поделим
![]()
Работа при
неизменяемом объёме равна нулю ![]()
При этом все тепло
идет на изменение внутренней энергии
![]()
![]() .
.
Из уравнения (1) при постоянном объеме изменение энтропии может
быть вычислено
![]() :
:![]()
Изобарный процесс:
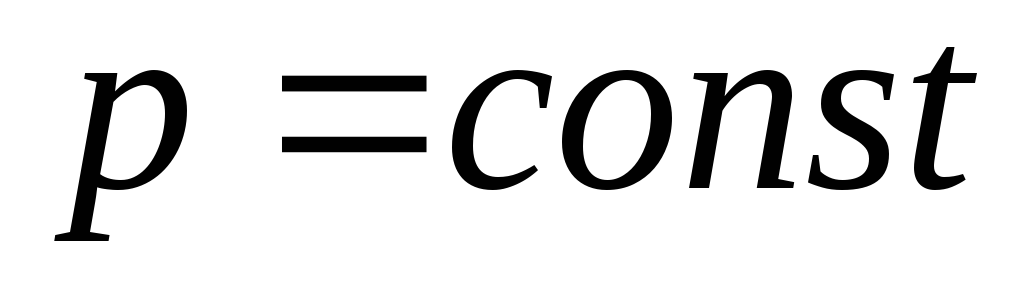
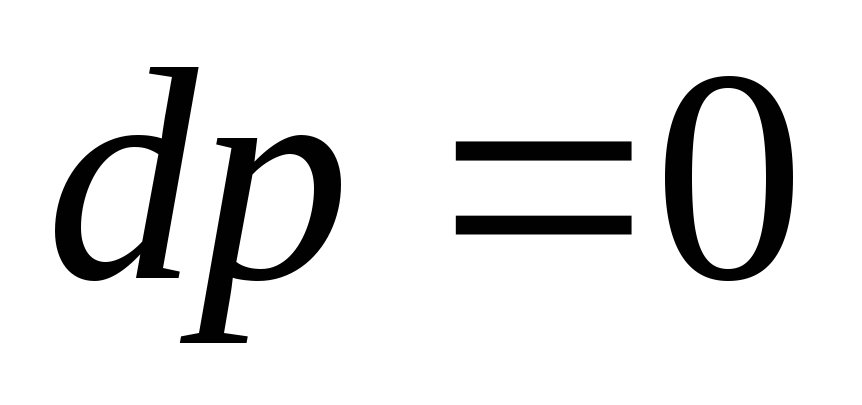 Для двух состояний идеального газа:
Для двух состояний идеального газа:
![]()
![]()
![]()
Работа при изобарном процессе:
![]()
![]()
При приращении
температуры на 1 градус
![]() работа равна газовой постоянной:
работа равна газовой постоянной:
![]()
По физическому
смыслу газовая постоянная R
есть работа расширения газа в обратимом
процессе при постоянном давлении
![]() и при нагревании газа на 1°
и при нагревании газа на 1°
![]()
![]()
![]()
![]() - уравнение Майера
- уравнение Майера
Из уравнения (1) и соотношения (2):
![]()
![]()
![]() Следует,
что энтропия в изобарном процессе может
быть вычислена:
Следует,
что энтропия в изобарном процессе может
быть вычислена:
![]()
![]()
![]()
![]() <
<
![]() т.к.
т.к.![]() <
<
![]()
При этом в координатах t-s изохора проходит круче изобары (см. рис.) .
Изотермический процесс:
![]()
![]()
![]()
![]()
![]()
Равнобочная гипербола (снова строчные символы)
![]()
![]()
![]() - для 1 процесса
- для 1 процесса ![]() - текущее значение
- текущее значение
![]()
![]()
![]()
![]()
![]()
![]()
Изменение энтропии
![]()

Адиабатный процесс: - без теплообмена c внешней средой
![]()
![]()
![]()
![]()
![]()
Работа расширения за счет изменения внутренней энергии
![]()
Используя (1) выведем
уравнение адиабаты в
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
k – показатель адиабаты
Неравнобочная гипербола


Соотношения между параметрами состояния и работой газа в адиабатном процессе.
![]()
p и V
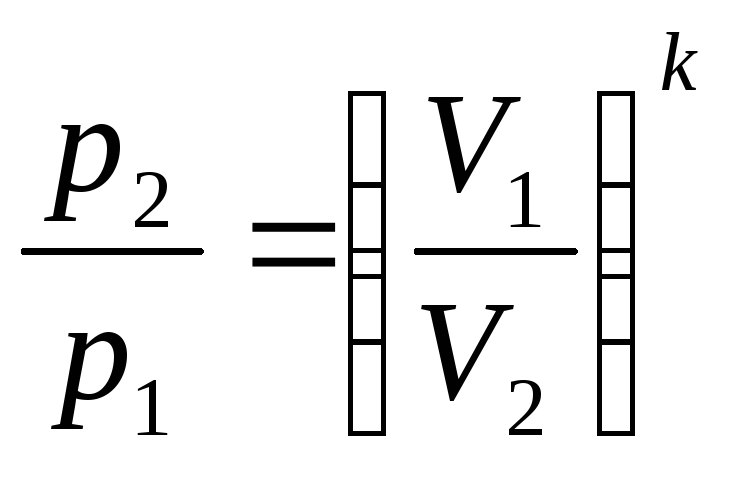 (1)
(1)
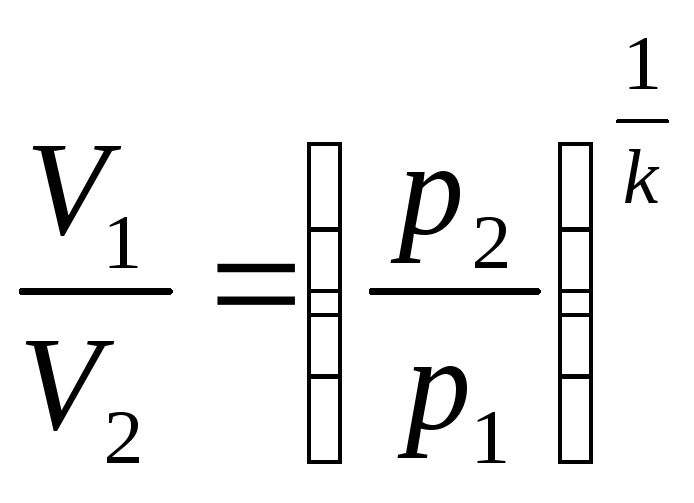 (2)
(2)
T и V
![]() (3)
(3)
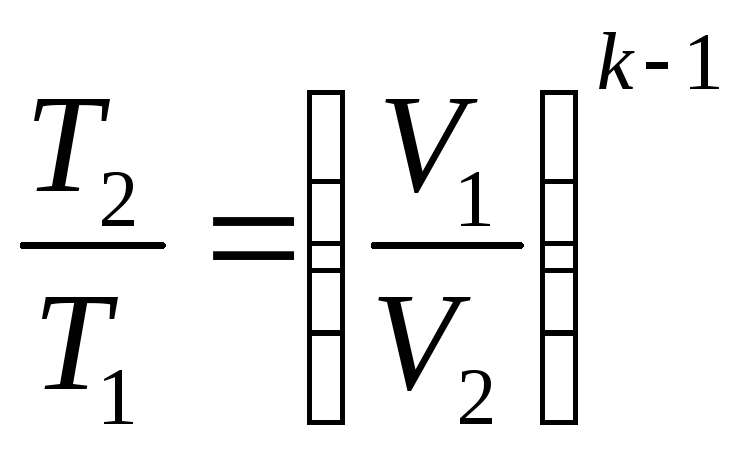 (4)
– из (1) и (3)
(4)
– из (1) и (3)
T и p
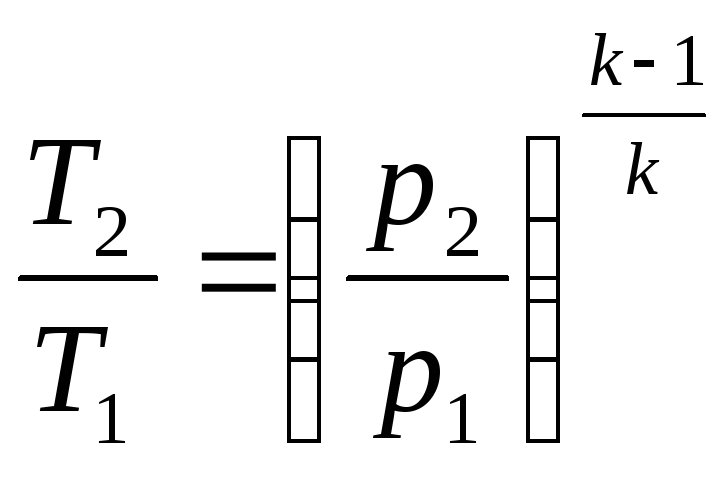 (5)
– из (2) и (3)
(5)
– из (2) и (3)
Изменение внутренней энергии газа:
![]() (6)
(6)
Работа газа:
![]() (7)
(7)
![]() подставляем
в (7)
подставляем
в (7)
![]()
![]() - подставим (4)
- подставим (4)
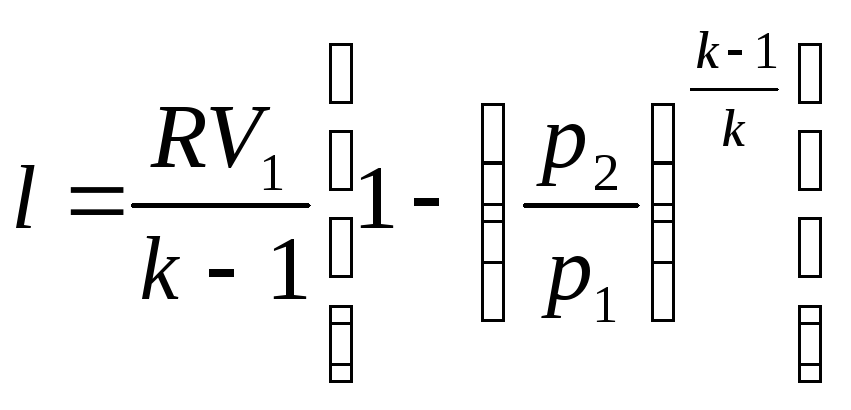
![]()
Пример: Воздух адиабатно расширяется от 780° до 200° С. Определить DU; l. Показать график процесса DU в диаграмме T-S.
![]() или
или
![]()
![]()

Политропные процессы
В политропных процессах изменение внутренней энергии в процессе пропорционально подводимому или отводимому теплу.
du = dq, (- ; +).
Если коэффициент = const – процесс называется политропный – это процесс, в котором доля тепла идущего на изменение внутренней энергии есть величина постоянная.
dq = du + I = dq +l
dq = CпdT , Сп – теплоемкость политропного процесса,
В общем случае изменение состояния рабочего тела характеризуется уравнением политропы:
![]() - уравнение
политропы, n
- показатель политропы
- уравнение
политропы, n
- показатель политропы
![]() для
данного процесса
для
данного процесса
Все ранее рассмотренные процессы есть частные случаи политропных
n=0
–
изобарный процесс ![]()
n=1
– изотермический процесс ![]()
n=k
– адиабатный процесс ![]()
n=¥
- изохорный процесс ![]()
При n< 0 давление увеличивается при расширении т.е. необходимо подводить тепла очень много. Этот процесс расположен в I и III квадрантах.
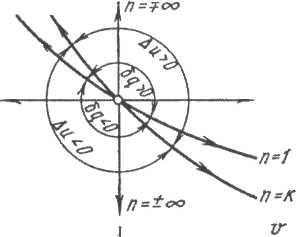
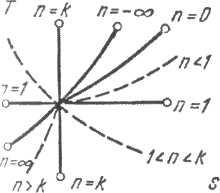

Имея такую диаграмму можно установить:
1. Совершается расширение или сжатие: V2 < V1 – сжатие
Как изменится внутренняя энергия газа:
![]() T2
<
T1
–
DU
<
0
T2
<
T1
–
DU
<
0
T2 > T1 – DU > 0
3. Подводится или отводится тепло: DS > 0 q > 0 – отводится
DS < 0 q < 0 – подводится
4. Знак теплоемкости:
![]() C
>
0 – для I
и III
квадрантов диаграммы T-S
C
>
0 – для I
и III
квадрантов диаграммы T-S
При исследовании политропных процессов возможно использование и других показателей, не только n, но и:
![]()
![]()
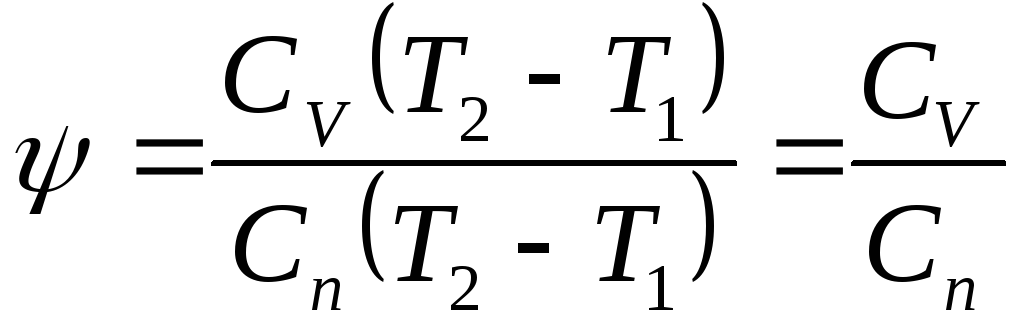
Теплоемкость газов в политропном процессе.
Установим связь между теплоемкостью и показателем политропы:
![]()
Для политропного процесса сохраняются все соотношения адиабатного, только вместо k ставится показатель политропы:
![]()
![]()
![]()
![]() - проанализируем
- проанализируем
а) n=k C=0
б) n=1 C=±¥
но если n=0.999… C=+¥
n=1.000…1 C=-¥
в) n=0 C=CP
г) n=¥ C=CV

![]()
![]()
![]()
![]()
Определение показателя политропы по графику процесса.
![]() возьмём логарифм
возьмём логарифм
![]()
![]()
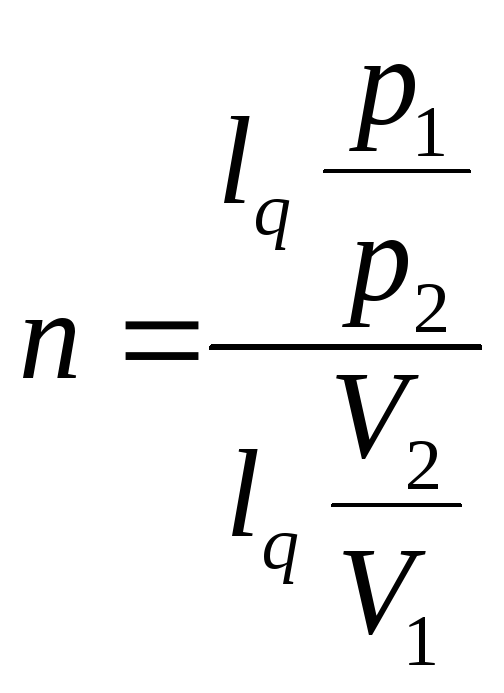
Особенность процессов в тепловых машинах.
Особенность тепловых машин: рабочее тело проходит через машину. Т.е. любая тепловая машина – проточная система. Поэтому необходимо ввести новые характеристики термодинамических процессов.

Рассмотрим общую схему тепловой машины, конкретно – тепловой двигатель. В трубопровод 1 поступает рабочее тело p1,V1,T1( и т.д. ). В машине М это тело деформируется, затем поступает в выпускной трубопровод 2 с параметрами p2, V2, T2 ( и т.д. ). К рабочему телу подводится тепло q, получается работа с выходного вала.
