
ВМ26
.pdf

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
Кафедра высшей математики
ПРАКТИКУМ ПО МАТЕМАТИКЕ
Часть 1
Методические указания
Печатаются по решению редакционно-издательского совета СГАСУ от 16.12.2013 г.
САМАРА
2014
1
УДК 51(076) П 69
Практикум по математике. Часть 1: методические указания / Cост.: М.Ю. Хлебникова,
П 69 Т.В. Шувалова. – Самара: СГАСУ, 2014. – 40 с.
В методические указания вошли все разделы математики, изучаемые студентами I курса всех специальностей в первом семестре. Сборник задач содержит справочный материал, основные теоретические положения, необходимые для решения задач и задания на аудиторные занятия. Задачи представлены по темам, систематизированы по методам решения, для некоторых приведены ответы. Также приведены варианты контрольных работ с ответами, что позволит студентам подготовиться к ним. Методические указания составлены в соответствии с рабочим планом кафедры высшей математики.
Рецензент – доцент кафедры ВМ СГАСУ, к.т.н. В.Г. Гумеров.
УДК 51(076)
©Хлебникова М.Ю., Шувалова Т.В., составление, 2014
©СГАСУ, 2014
2
Введение
Это пособие предназначено для студентов первого курса. В «Практикуме по математике» подобраны и методически распределены задачи по темам, изучаемым ими в первом семестре по математике.
В начале каждого раздела приведены формулы, определения и другие краткие пояснения теории, необходимые для решения последующих задач, в конце раздела имеются ответы. В пособие включены также разделы математики, которые должны быть изучены студентами самостоятельно. В конце каждой темы приведены варианты контрольных работ с ответами.
Безусловно, работа с пособием потребует от студентов не только определенных математических знаний и настойчивости, но и даст им возможность почувствовать радость самостоятельного открытия.
3

1. Функция, ее область определения и значений, график и свойства
Переменная y называется функцией переменной x 

 , если каждому значению x поставлено в соответствие одно и только одно значение y, принадлежащее некоторому множеству Y. Областью определения D(y) функции у = f (x) называется множество всех значений аргумента х, для которых выражение f (x) определено (имеет смысл), т. е. D(y)=Х.
, если каждому значению x поставлено в соответствие одно и только одно значение y, принадлежащее некоторому множеству Y. Областью определения D(y) функции у = f (x) называется множество всех значений аргумента х, для которых выражение f (x) определено (имеет смысл), т. е. D(y)=Х.
Области определения основных элементарных функций
Область определения любого многочлена – R,


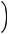







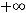
 ;
; 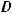
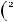



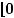


 ;
;
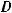





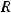 ;
; 






 ;
; 



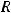 ;
;


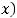





 ;
; 







 ;
;



 ,
,
; |
|
; |
|








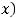

 .
.
Множеством(областью)значенийЕ(у)функцииy = f (x)называетсямножествовсехтаких чисел yо , для каждого из которых найдется число xо такое, что f (xо ) = yо , т. е. Е(у)=Y.
Области значений основных элементарных функций
Областьюзначенийвсякогомногочленачетнойстепениявляетсяпромежуток[т, + ∞),где т – наименьшее значение этого многочлена, либо промежуток (-∞, п], где п – наибольшее значение этого многочлена. Областью значений всякого многочлена нечетной степени является R.
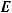

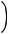

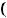






 ;
; 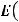
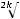


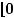

 ;
;
; |
|
|
; |
; |
|
|
; |
|
; |
|
|


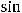






 ;
; 






 ;
;







 ;
; 



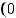

 .
.
Графикомфункцииу = f (x) называетсямножествовсехточекплоскостискоординатами
(x ; f (x)), где 
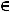
 .
.
Функция у = f (x) называется четной, если ее область определения D(y) симметрична относительно начала координат и для любого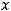

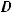
 верно равенство f (-x) = f (x). График четной функции симметричен относительно оси OY. Функция у = f (x) называется нечетной, если ее область определения D(y) симметрична относительно начала координат и для любого
верно равенство f (-x) = f (x). График четной функции симметричен относительно оси OY. Функция у = f (x) называется нечетной, если ее область определения D(y) симметрична относительно начала координат и для любого 

 верно равенство f (-x) = –f (x). График нечетной функции симметричен относительно начала координат.
верно равенство f (-x) = –f (x). График нечетной функции симметричен относительно начала координат.
Функция, не являющаяся ни четной, ни нечетной, называется функцией общего вида.
Функция у = f (x) называетсяпериодической, если существует число Т ≠ 0,чтодлялюбого



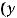
 выполняется равенство:
выполняется равенство:






 .
.
4
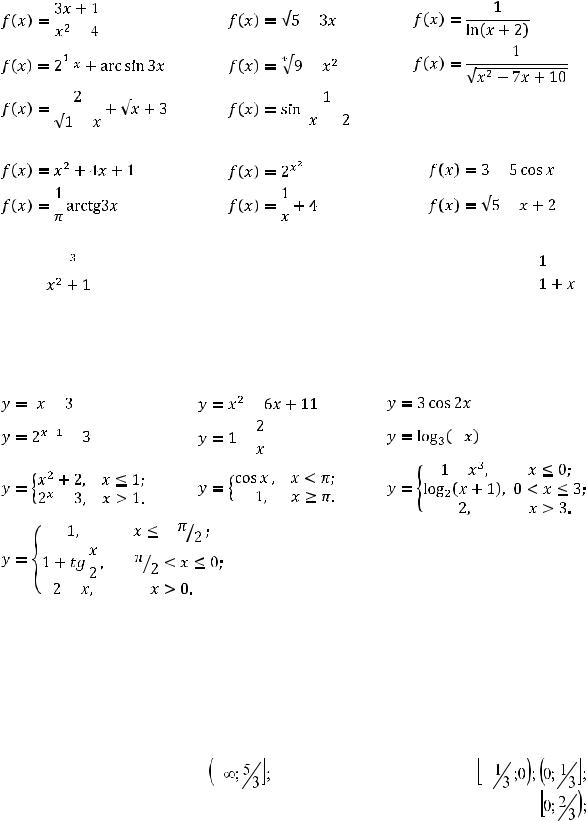
|
|
|
|
|
|
|
|
|
|
|
Задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдите область определения функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1.1. |
|
|
|
|
|
; |
|
|
1.2. |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
1.3. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1.4. |
|
|
|
|
|
|
|
|
|
|
1.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.6. |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
1.7. |
|
|
|
|
|
; |
1.8. |
|
|
|
|
|
|
|
|
; |
1.9. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
;
;

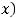







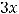
 .
.
Найдите множество значений функций:
1.10. |
; |
1.11. |
; |
1.12. |
|
|
; |
|||||
|
||||||||||||
1.13. |
|
; |
1.14. |
|
; |
1.15. |
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||
|
|
|
||||||||||
Определите, какие из следующих функций четные, какие – нечетные, а какие – общего вида:
1.16. 


 ; 1.17.
; 1.17. 






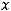
 ; 1.18.
; 1.18. 
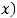

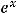

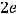
 ; 1.19.
; 1.19. 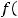



 .
.
Определите, является ли данная функция периодической, найдите ее наименьший положительный период, если он существует:
1.20. |
f (x)= sin 4x +5; |
1.21. |
|
f (x)= cos2 5x; |
|
|
|
1.22. |
f (x)= x2 . |
||||||||||||||||||||||||||||||||||||||||||||||||
Постройте график функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1.23. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
1.24. |
|
|
|
|
|
|
|
|
; |
|
|
1.25. |
|
; |
|
|
|
|
||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
1.26. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
1.27. |
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
1.28. |
|
|
|
; |
|
|
|
|||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1.29. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.30. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.31. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1.32. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дополнительные задачи |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Постройте графики функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = arcsin(sin 2x); |
|||||||||||||||||||||||||||||||||||
1.33. |
y = |
|
|
|
x |
|
− 2 |
|
; |
1.34. |
|
y = сos2 x; |
|
|
|
1.35. |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
1.36. |
y = sign(cos x); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = 0,5 |
x+1 |
||||||||||||||||||||||||||||
1.37. |
|
y = |
|
x |
|
+ |
|
x +1 |
|
+ |
|
x + 2 |
|
; |
1.38. |
x |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОТВЕТЫ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1.1. (–∞;–2); (–2;2); (2;+∞); 1.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
1.3. (−2;−1)(; −1;+∞); |
1.4. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
1.5. [–3;3]; 1.6. (–∞;2); (5;+∞); 1.7. [–3;1); 1.8. (–∞;–2); (–2;2); (2;+∞); 1.9. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1.10. |
[–3;+∞); 1.11. |
[1;+∞); 1.12. |
[–2;8]; 1.13. |
(–0,5;0,5); 1.14. (–∞;4); (4;+∞); |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
1.15. [2;+∞); 1.16. нечетная; 1.17. четная; 1.18. функция общего вида; 1.19. нечетная;
1.20. T = π2 ; 1.21. T = π5 ; 1.22. непериодическая.
5
|
|
|
|
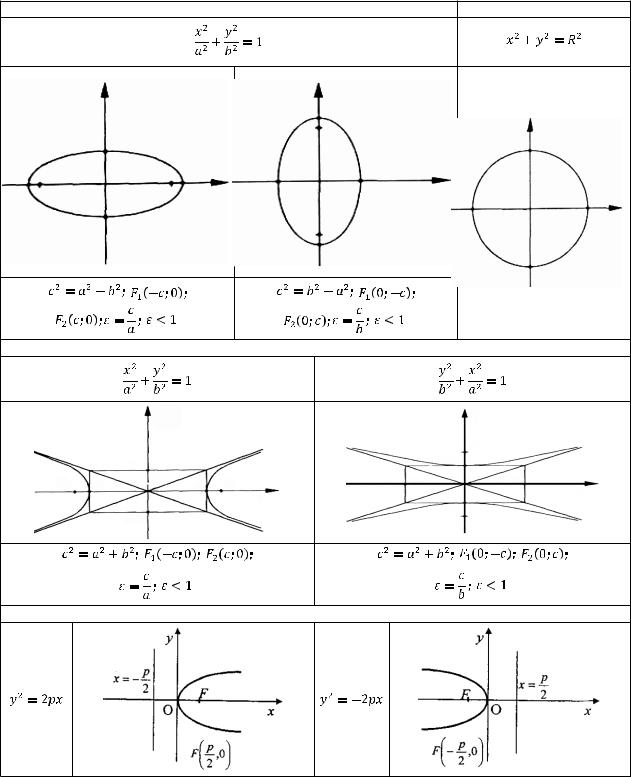
2. Кривые второго порядка |
|
|
|
|||
|
Линии, определяемые алгебраическими уравнениями второй степени относительно |
|||||||||
переменных x и y, то есть уравнениями вида: |
|
|
|
|
|
|||||
|
|
|
Ax2 + 2Bxy +Cy2 + 2Dx + 2Ey + F = 0, |
(A2 + B2 +C 2 |
≠ 0), |
|
||||
называются кривыми второго порядка. |
|
|
|
|
|
|||||
|
|
|
|
|
Эллипс |
|
|
|
Окружность |
|
|
|
|
y |
|
y |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
F2 |
|
|
|
y |
|
-a |
F1 |
|
F2 |
a |
-a |
a |
x |
|
|
|
|
|
0 |
|
x |
0 |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-b |
|
|
F1 |
|
|
|
0 |
x |
|
|
|
|
|
-b |
|
|
|
|
|
|
|
|
|
. |
|
|
. |
|
|
|
|
|
|
|
|
Гипербола |
|
|
|
|
|
|
|
|
y |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
F2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
F1 |
-a |
0 |
a |
F2 |
|
-a |
a |
|
|
|
|
|
|
x |
|
|||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
-b |
|
|
|
|
|
|
-b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
. |
|
|
|
|
|
|
Парабола |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|

Задачи
Приведите уравнение к каноническому виду, определите вид кривой и постройте ее в исходной системе координат:
2.1. |
|
|
|
|
|
|
|
|
|
|
|
. |
2.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2.3. |
|
|
|
|
|
|
|
|
|
|
|
|
. |
2.4. |
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2.5. |
|
|
|
|
. |
|
|
|
|
2.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Какие линии определяются следующими уравнениями: |
|
|
|
|
|||||||||||||||||||||||||||
2.7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2.9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Постройте линии в полярной системе координат, изменяя φ от 0 до 2π с интервалом π/8. Перейдите в декартову систему координат и определите вид кривой:
2.11. |
2.12. |
|
|
|
|
|
; |
|||
|
|
|
|
|
||||||
2.13. |
|
|
|
2.14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Дополнительные задачи
2.15.Составьте уравнение эллипса, фокусы которого расположены на оси OХ, симметрично относительно начала координат, зная что 



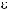



2.16.Составьте уравнение гиперболы, если ее фокусы лежат на оси OY и расстояние между ними равно 10, а длина действительной оси равна 8.
2.17.Парабола симметрична относительно оси OХ, ее вершина находится в начале координат. Составьте уравнение параболы, зная, что она проходит через точку А(-3;-3).
2.18.Трос, подвешенный за два конца на одинаковой высоте, имеет форму дуги параболы. Расстояние между точками крепления 24 м. Глубина прогиба троса на расстоянии 3 м от точки крепления равна 70 см. Определите глубину троса посередине между крепления.
ОТВЕТЫ
2.1. |
(x +2)2 |
|
|
(y −3)2 |
|
2.2. |
|
(x −2) |
2 |
+(y +3) |
2 |
=10; |
|
|
2.3. |
(x −2)2 |
(y −3)2 |
=1; |
|||||||
|
|
|
+ |
|
|
=1; |
|
|
|
|
|
|
− |
|
|||||||||||
4 |
|
|
9 |
|
|
|
|
9 |
4 |
||||||||||||||||
2.15. |
|
x2 |
+ |
|
y2 |
=1; |
2.16. |
|
y2 |
− |
x2 |
=1; |
2.17. |
y |
2 |
= −3x; |
2.18. |
1,6 |
м. |
||||||
100 |
64 |
16 |
9 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7

3. Предел функции
Число b называется пределом функции y = f (x) при x→a (т.е. 




 ), если для
), если для
всех значений х, достаточно близких к числу а, соответствующие значения y = f (x) будут как угодно мало отличаться от b. Можно находить предел функции f (x), когда х стремится к своей предельной точке a только слева, и тогда получим левосторонний предел f (x),
который обозначается |
|
. Аналогично при х, стремящемся к a справа, |
||
|
||||
|
|
|
|
|
определяется правосторонний предел |
Эти пределы функции назы- |
|||
ваются односторонними.
Функция f(x) имеет при x→a предел, если 


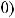


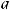
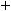





 . Если элементарная функция f (x) определена в точке x = a, тo
. Если элементарная функция f (x) определена в точке x = a, тo 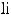

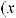



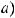 .
.
Число b называется пределом функции f (x) при x→a (
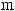



 ), если для произвольно
), если для произвольно 
 малой окрестности
малой окрестности 
 точки b существует (
точки b существует (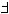 ) такая окрестность
) такая окрестность 
 точки a, что для всех
точки a, что для всех 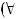


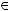

 значения
значения 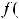



 , или:
, или:




 .
.
Функция y = f (x) называется бесконечно большой при x→a, если 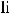




 (или +∞,
(или +∞,
или -∞), ∞ – символ бесконечно большой функции. Функция y = f (x) называется бесконечно малой при x→a, если 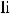




 0 – символ бесконечно малой функции. Функция y = f (x)
0 – символ бесконечно малой функции. Функция y = f (x)
называется ограниченной на множестве X, если  и
и  такие, что при
такие, что при 




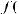


 .
.
Операции с бесконечно малыми, ограниченными и бесконечно большими функциями
Сложение |
Умножение |
|
|
|
Деление |
Возведение в степень |
||||||||||||
+∞+∞=+∞ |
C·0=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
-∞-∞=-∞ |
C·∞=∞ при C≠0 |
|
|
|
при C≠0 |
|
|
|
|
|
|
|
||||||
∞+C=∞ |
∞·∞=∞ |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Не определено |
Не определено |
|
|
|
Не определены |
Не определены |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правила вычисления пределов:
1. |
. |
2. |
. |
3.
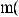





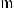




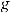 , кроме случая
, кроме случая 

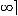 .
.
4.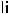
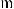


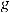

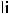



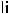

 , кроме случая
, кроме случая 

 .
.
5.

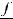

 , кроме случаев
, кроме случаев
 и
и
 .
.
6.





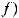

 , кроме случаев
, кроме случаев




 .
.
7.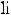

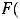





 , если
, если 


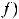 , конечный или бесконечный.
, конечный или бесконечный.
8

Задачи |
|
|
3.1. Найдите: |
|
|
; |
; |
; |
|
|
; |
|
|
. |
3.2. Найдите: |
; |
; |
|
||
|
; |
; |
|
|
; |
|
; |
. |
Вычислите данные пределы: |
|
|
3.3. |
|
|
|
|
|
|
|
|
|
; |
|
|
|
; |
3.4. |
|
|
|
; |
3.5. |
|
|
|
|
|
|
|
|
|
; |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3.6. |
|
|
|
|
3.7. |
|
|
|
|
; |
3.8. |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С помощью графиков основных элементарных функций найдите:
3.9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
3.10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
3.13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; 3.15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.16. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
3.17. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.18. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.19. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
3.21. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
3.22. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.23. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.24. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Вычислите пределы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
3.25. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.26. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.27. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.28. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3.29. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.30. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.31. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.32. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОТВЕТЫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3.1. -2; 0; 0; 2; |
|
+∞; 3.2. 0; 0; |
-2; |
|
|
|
0; +∞; |
-2; -; |
3.3. 1,5; |
3.4. |
|
|
|
; |
3.5. 31; 3.6. -12; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.7. |
|
|
; 3.8. |
|
|
|
|
|
|
|
|
|
; 3.9. 0; 3.10. π; 3.11. +∞; 3.12. -∞; 3.13. +∞; 3.14. 1; 3.15. 0; 3.16. -∞; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.17. |
-∞; 3.18. |
+∞; 3.19. +∞; |
|
3.20. -∞ 3.21. 0; 3.22. -; |
|
3.23. 0; 3.24. -∞; 3.25. -4; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.26. |
|
|
3.27. |
|
-0,5; 3.28. |
|
|
|
0,5; |
|
3.29. |
0,25; |
|
3.30. |
|
|
|
|
|
3.31. |
|
3.32. 1,5. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9
