Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Физика2сем / Касаткина И_Л - Решебник по физике

.pdf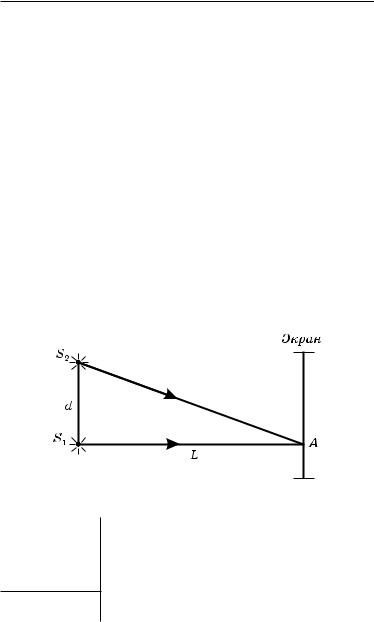

Скачиваний:

4837

Добавлен:

29.03.2015

Размер:

4.61 Mб

Скачать

☆

<<< < Предыдущая 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 5253 / 6153 54 55 56 57 58 59 60 61 > Следующая >>>

Решебник по физике

Выразим все величины в единицах СИ: 4 см = 0,04 м, 50 см = 0,5 м, 80 см = 0,8 м.

Произведем вычисления:

D =	1		+	0,8	дптр = 42 дптр.
		1
	0,5			0,04

Ответ: D = 42 дптр.

Задача 43. Длина волны, испускаемой двумя когерентными источниками света S1 и S2, λ = 4 · 10–7 м, расстояние между ними d = 0,3 см, расстояние от каждого источника до экрана 9 м. Спрашивается, максимум или минимум интерференции будет наблюдаться на экране под источником света S1.

Обозначим L расстояние от источника до экрана, ∆d — разность хода световых волн от источников до точки А на экране, где происходит интерференция, k — число полуволн, укладывающихся в этой разности хода. Выполним чертеж (рис. 194).

Дано:

λ = 4 · 10–7 м d = 0,3 см L = 9 м

k — ?

Рис. 194

Решение

Максимум освещенности в точке А будетнаблюдаться,есличислополуволн k, содержащихся в разности хода волн, будет четным. А если оно будет нечетным, то в точке А будет наблюдаться минимум.

520

4. Колебания и волны. Оптика. Теория относительности, атомная физика

Число k равно отношению разности хода к длине полуволны:

k = 0∆,5dλ.

Разность хода найдем путем вычитания из отрезка AS2 отрезка AS1:

∆d = AS2 − AS1= AS2 − L.

Отрезок AS2определим по теореме Пифагора:

AS = d2	+ L2 .
2

С учетом этого

∆d = d2 + L2 −L.

Нам осталось подставить правую часть этого выражения в первую формулу:

	k =	d2 + L2 −L		.

		0,5λ
Произведем вычисления:
k =	(3 10−3 )2 +92 −9
			= 2 — четное число.
	0,5 4 10−7

Значит, под источником света S1 будет максимум — светлое пятно.

Ответ: k = 2 — максимум.

Задача 44. Период дифракционной решетки d = = 1,2 · 10–3 см, угол между спектрами второго и третьего порядков ∆ϕ = 2° 30′. Определите длину монохроматической волны.

Обозначим j1 угол дифракции, соответствующий спектру второго порядка, j2 — угол дифракции, соответствующий спектру третьего порядка, k1 и k2 − порядок спектров, λ — длину световой волны.

521

	Решебник по физике

Дано:		Решение
Дано:		Решение
d = 1,2 · 10–3 см		Согласно условию максимума на
k1 = 2	дифракционной решетке
k2 = 3	d sin ϕ1 = k1λ и d sin ϕ2= k2λ.
∆ϕ = 2° 30′	d sin ϕ1 = k1λ и d sin ϕ2= k2λ.
∆ϕ = 2° 30′			Здесь j2 = j1 + ∆j, поэтому

λ — ?
λ — ?				dsin(j1 + ∆j) = k1λ .
Отсюда				dsin(j1 + ∆j) = k1λ .
Отсюда
	sinj			= k		λ	(1)
			1	1 d
и	sin(j + ∆j) = k						λ .
		1				2 d
Преобразуем сумму синусов двух углов:
sin(j1 +∆j) = sinj1 cos∆j+cosj1 sin∆j,
где cosj = 1−sin2 j .
1	1
Теперь учтем, что sin		2				λ	2
Теперь учтем, что sin			j = k				≈ 0, т.к. угол дифрак-
			1		1 d

ции всегда мал. Тогда получим:

sin(j1 + ∆j) ≈ sinj1 cos∆j+sin∆j ≈ k2 dλ

или с учетом (1)

k1 dλcos∆j+sin∆j = k2 dλ.

Поскольку при малых углах cos ∆j ≈ 1,

то	k λ	−k λ	= sin∆j,	λ	(k −k ) = sin∆j,
	2 d	1 d		d	2 1
откуда			λ = dsin∆j.
			k −k
				2	1

522

Дано:

N = 2000 l = 4 мм

λ = 0,4 мкм m — ?

4.Колебания и волны. Оптика. Теория относительности, атомная физика

Произведем вычисления:

λ = 1,2 10−3 sin2°30′ м = 5,2∙10–5 см = 5,2∙10–7 м. 3−2

Ответ: λ = 5,2∙10–7 м.

Задача 45. Дифракционная решетка имеет 2000 штрихов на длине 4 мм. На нее нормально к ее поверхности падает параллельный пучок лучей с длиной волны 0,4 мкм. Найти общее число максимумов, даваемое этой решеткой.

Обозначим N число штрихов на длине l, λ — длину волны, m — общее число максимумов, даваемое этой решеткой, d — период решетки, j — угол дифракции, k — порядок максимума, kmax — порядок последнего максимума.

Решение

Чтобы найти общее число максимумов по обе стороны от нулевого максимума на экране, надо сначала определить порядковый номер последнего максимума kmax. Для этого применим условие

максимума на дифракционной решетке:

d sin j = kλ.

(1)

Здесь d — период решетки. Его можно найти, разделив длину l, на которой помещается N штрихов, на их количество:

d =	l	.	(2)

	N

Последниймаксимумсоответствуетмаксимальномууглу дифракции j. А угол дифракции не может быть больше 90°. Значит, из формулы (1) следует, что

k = dsin90°							= d
	max			λ			λ
	max
или с учетом (2)
		k	=		l	.	(3)
		k	=			.	(3)
		max			Nλ

523

Решебник по физике

Поскольку симметричные максимумы, начиная с первого и кончая kmax, наблюдаются по обе стороны от нулевого, то для подсчета общего количества максимумов их надо удвоить и к ним еще прибавить центральный нулевой максимум, поскольку в формуле (1) порядковый номер максимума k начинается с единицы. Поэтому общее число максимумов m равно:

m = 2kmax + 1

или с учетом (3)

m = 2Nlλ +1.

Выразим все величины в единицах СИ: 4 мм = 4 ∙ 10–3 м, 0,4 мкм = 7 ∙ 10–7 м.

Произведем вычисления:

m = 2	4 10−3	+1=11.
	2000 4 10−7

Отметим, что число, полученное от деления l на Nλ, которое в нашем случае равно 5,71, нельзя округлять по максимуму, т.е. до 6, т.к. в этом случае получится, что sin j> 1, что не имеет смысла.

Ответ: m = 11.

Задача 46. Звезда каждую секунду теряет световую энергию 1,8 ∙ 1026 Дж, и при этом ее масса уменьшается на k ∙ 108 кг. Чему равен коэффициент пропорциональности k?

Обозначим ∆Е потерянную энергию, ∆m — уменьшение массы звезды, c — скорость света в вакууме, k — коэффициент пропорциональности.

Дано:

∆Е = 1,8 ∙ 1026 Дж ∆m = k ∙ 108 кг

с = 9 ∙ 1016 м/с

k — ?

Решение

Согласно формуле∆Е=∆mc2 излученная звездой энергия пропорциональна изменению ее массы.

Значит,

1,8 ∙ 1026 = k ∙ 108 ∙ 9 ∙ 1016,

524

4. Колебания и волны. Оптика. Теория относительности, атомная физика

			1,8 1026
откуда	k =					= 20.
		10		8	16
					9 10

Ответ: k = 20.

Задача 47. Масса движущегося электрона превышает его массу покоя в 40 000 раз. С какой скоростью движется электрон?

Обозначим m массу движущегося электрона, m0 — его массу покоя, с — скорость света в вакууме, v — скорость электрона.

Дано:

Решение

m = 40 000 m0

Запишемформулузависимостимас-

с = 3 ∙ 108 м/с

сы электрона от его скорости:

v — ?

m =

1− v2

Отсюда определим скорость электрона:

1−

=1−

1−

откуда

v = c

1−

Произведем вычисления:

v = 3∙108 1−	1	см/с ≈ 299 999 999,9 м/с.

	2
	40000

Ответ: v = 299 999 999,9 м/с.

525

Решебник по физике

Задача 48. Масса воды до нагревания была равна 1 кг. Воду нагрели на 50 К. На сколько увеличилась масса воды в результате нагревания?

Обозначим m0 массу воды до нагревания, ∆m — изменение ее массы, cТ — удельную теплоемкость воды, ∆Т — изменение ее температуры, Q — полученное водой количество теплоты, ∆E — изменение энергии воды, с — скорость света в вакууме.

Дано:

m0 = 1 кг ∆Т = 50 К

сТ = 4200 Дж/(кг ∙ К) с = 3 ∙ 108 м/с

∆m — ?

Решение

При нагревании воды переданное ей количество теплоты идет на увеличение энергии воды:

Q = ∆E,

где Q = cTm0∆T и	∆Е = ∆mc2.
Приравняв правые части этих формул, получим:
	cTm0∆T = ∆mc2,
	∆m =	c m ∆T
откуда			T 0	.
		2
			c
Произведем вычисления:
∆m =	4200 1 50		кг = 2,3 · 10–12		кг.

	9 1016

Ответ: ∆m = 2,3 · 10–12 кг.

Задача49.Длинасветовойволнывнекоторойпрозрачной среде равна 3,0 · 10–7 м, энергия фотона в ней 4,4 · 10–19Дж. Определить абсолютный показатель преломления этой среды.

Обозначим v скорость света в этой среде, n — абсолютный показатель преломления среды, c — скорость света в вакууме, h — постоянную Планка, ν — частоту световой волны.

526

4. Колебания и волны. Оптика. Теория относительности, атомная физика

Дано:	Решение

E = 4,4 · 10–19 Дж	Показатель преломления ра-
λ = 3,0 · 10–7 м	вен отношению скорости света
c = 3 · 108 м/с	в вакууме к скорости света в
h = 6,62 · 10–34 Дж · с	данной среде:
		c
n — ?	n =
			.
		v
Скорость света в данной среде найдем из формулы дли-
ны волны:
	λ = v,
	ν
откуда	v = νλ.

Подставим это равенство в предыдущую формулу:

n =	c	.	(1)

	νλ

Частоту световой волны найдем из формулы Планка:

E = hν, откуда
		ν=	E.			(2)
			h
Подставив (2) в (1), мы решим задачу в общем виде:
		n =	ch	.
		n =		.
			λE
Произведем вычисления:
n	=	3 108 6,62 10−34			= 1,5.
n	=	3,0 10−7 4,4 10−19			= 1,5.
		3,0 10−7 4,4 10−19

Ответ: n = 1,5.

Задача 50. Работа выхода электронов из металла А = = 7,6 · 10−19 Дж,ихкинетическаяэнергияWK =4,5 · 10−20 Дж. Определить длину световой волны λ, падающей на металл.

Обозначим h постоянную Планка, ν — частоту, c — скорость света в вакууме.

527

Решебник по физике

Дано:

WK = 4,5 · 10−20 Дж А = 7,6 · 10−19 Дж

h = 6,62 · 10−34 Дж · с с = 3 · 108 м/с

λ — ?

Решение

По формуле Эйнштейна для фотоэффекта энергия фотона, падающего на металл, расходуется на работу выхода электрона из металла и на сообщение ему кинетической энергии:

hν = А + WK.

(1)

Теперь запишем формулу длины волны, выразив ее через частоту:

λ =

(2)

Выразим из (1) частоту и подставим ее в (2):

ν =

A +WK

и тогда

λ =

A +W .

Произведем вычисления:

λ =

3 108

6,62 10−34

м ≈ 2,5 · 10–7

м.

7,6 10−19 +4,5 10−20

Ответ: λ = 2,5 ∙ 10–7 м.

Задача 51. Работа выхода электрона из металла А = = 3,3 · 10–19 Дж. Определить красную границу фотоэффекта

νmin.

Обозначим h постоянную Планка.

Дано:

А = 3,3 · 10–19 Дж

h = 6,62 · 10−34 Дж · с

νmin — ?

Решение

Красную границу фотоэффекта определим, приравняв энергию фотона работе выхода электрона из металла:

hνmin = A,

528

4. Колебания и волны. Оптика. Теория относительности, атомная физика

откуда	νmin =	A	.

		h

Произведем вычисления:

ν = 3,3 10−19 Гц ≈ 5 · 1014 Гц. min 6,62 10−34

Ответ: νmin = 5 ∙ 1014 Гц.

Задача 52. Длина волны фотона, падающего на металл, λ=3,0 · 10−7 м,краснаяграницафотоэффектаνmin =4,3 · 1014 Гц. Определить кинетическую энергию фотоэлектронов.

Обозначим WK кинетическую энергию фотоэлектронов, h — постоянную Планка, A — работу выхода электронов, ν — частоту падающей на металл волны, c — скорость света в вакууме.

Дано:

λ = 3,0 · 10−7 м

νmin = 4,3 · 1014 Гц h = 6,62 · 10−34 Дж · с

с = 3 · 108 м/с

WK — ?

Решение

Кинетическую энергию фотоэлектронов найдем из формулы Эйнштейна для фотоэффекта:

	hν = A + WK,
откуда
WK = hν – A.	(1)

Частоту выразим через длину волны, падающей на ме-

талл: λ = νc , откуда

ν =	c
ν =	λ .	(2)

Работу выхода определим через красную границу фотоэффекта:

А = hνmin.

Подставим (2) и (3) в (1):

	c	c
WK = h		– hνmin = h
	λ

		λ

(3)

−ν
−ν	.
	min

529

<<< < Предыдущая 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 5253 / 6153 54 55 56 57 58 59 60 61 > Следующая >>>