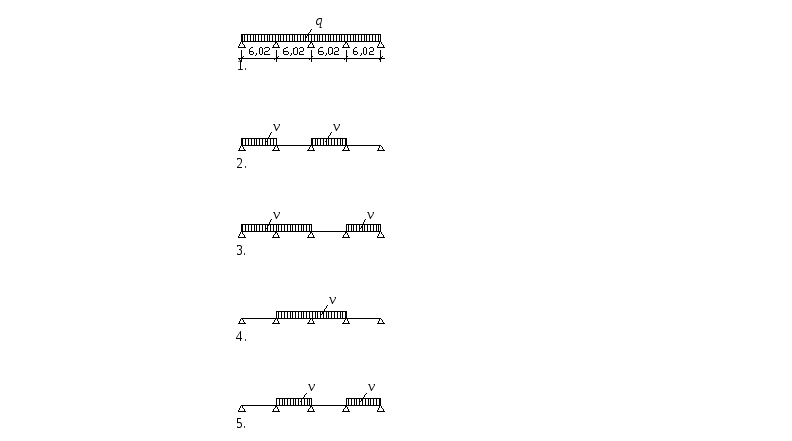
2. Расчет неразрезного ригеля.

Ригель представляет собой неразрезную многопролетную (четырехпролетную) конструкцию со свободным (шарнирным) опиранием концов на кирпичные стены здания.

Проектируем ригель сборно-монолитной конструкции с соединением на монтаже однопролетных сборных элементов в неразрезную систему путем сварки выпусков арматуры из колонн и ригелей и замоноличивания стыков, а в дальнейшем – и швов между сборными панелями

Ригель после сварки арматуры и замоноличивания стыков превращается в элемент поперечной рамной конструкции, однако при свободном опирании его концов на стены и равных или отличающихся не более чем на 10 % расчетных пролетах ригель разрешается рассчитывать как неразрезную многопролетную балку

Расчетные пролеты, м:

крайний

средний

Соотношение расчетных пролетов

Нагрузка на ригель от сборных панелей передается продольными ребрами сосредоточенно. Для упрощения расчета без большой погрешности при четырех и более сосредоточенных силах на длине пролета разрешается заменять такую нагрузку эквивалентной (по прогибу), равномерно распределенной по длине ригеля. Принимаем ригель сечением 3070 см.

Нагрузки на ригель, кН/м:

Нормативные	Расчетные
Постоянные:
от веса пола и панелей от веса ригеля 250,30,70=5,25 Итого постоянная gn=20,9 Временная vn =11*5,44=59,84	5,251,1=5,775 g=23,18 v=59,841,2=71,8

Полная нагрузка на ригель:

нормативная g_n + v_n = 20,9+59,84=80,74,

расчетная g + v =23,18+71,8=94,98

Кратковременно действующая часть нагрузки на ригель: ;

расчетной нагрузки

Длительная действующая часть расчетной нагрузки на ригель: g_l+v_l =94,98-9,8=85,18 кН/м

(g_l+v_l)/(g+v) =85,18/94,98=0,897<0.9, поэтому γ_b1=1.0.

Изгибающие моменты в сечениях ригеля по его длине определяются по формуле а поперечные силы на опорах ригеля – по формуле

где g и v – соответственно постоянная и временная нагрузки на ригель;  и  - коэффициенты, принимаемые в зависимости от числа пролетов и схемы загружения; l – расчетный пролет, крайний или средний. Для определения изгибающего момента на опоре В принимают

Моменты и поперечные силы в сечениях ригеля определяются с учетом коэффициента надежности по ответственности γ_n=0,95, на который умножаются внутренние силы.

Ординаты эпюр изгибающих моментов и поперечных сил при всех возможных схемах загружения пролетов ригеля временной нагрузкой и расчете по «упругой» схеме приведены в, от загружения ригеля постоянной нагрузкой в сочетании с невыгодным его загружением временной нагрузкой строятся эпюры моментов и поперечных сил, а по максимальным значениям усилий иногда строят так называемую огибающую эпюру. Следует отметить, что при дальнейшем перераспределении усилий вследствие пластических деформаций бетона и арматуры пользоваться огибающей эпюрой нельзя. Перераспределение усилий производится только для отдельных схем загружения по соответствующим эпюрам M и Q.

В связи с жесткими требованиями к размещению в опорных сечениях ригеля выпусков арматурных стержней, стыкуемых ванной сваркой, следует стремиться к уменьшению площади сечения опорной арматуры и числа стержней в опорных сечениях, а также к унификации армирования опорных сечений. Достигается это перераспределением усилий между опорными и пролетными сечениями вследствие пластических деформаций бетона и арматуры. При этом уменьшение опорных моментов не должно превышать 30 % в сравнении с рассчитанными по «упругой» схеме.

При уменьшении опорного момента на опорах В на 30 % принимаем максимальную ординату добавочной треугольной эпюры 0,3M^B_max , а с целью унификации армирования опорных сечений момент на опоре С уменьшаем до 0,7M^B_max . Максимальная ордината добавочной эпюры .

Расчеты по определению изгибающих моментов и поперечных сил сведены в табл. 3; расчеты по перераспределению усилий в неразрезном ригеле – табл. 4.

Таблица 3

Схемы загружения	Изгибающие моменты, кНм													Поперечная сила, кН
	МА	В крайних пролетах					МВ	В средних пролетах					МС	QA	QВл	QВп	QСл
		М1	М2	М3	М4	М5		М6	М7	М8	М9	М10
	0,0	51,2	67,4	62,4	48,7	-5,0	-101,0	-20,3	27,5	36,2	34,8	14,5	-72,5	54,5	-84,2	80,1	-69,4
	0,0	187,6	266,9	265,9	238,0	100,4	-156,6	-157,2	-145,9	-140,3	-134,9	-123,6	-112,3	191,7	-238,1	8,3	8,3
	0,0	151,3	194,4	175,2	129,1	-44,4	-352,1	-62,9	127,4	175,5	192,1	130,8	-56,3	162,9	-266,9	279,3	-183,9
	0,0	-19,2	-38,7	-48,5	-57,9	-77,4	-104,3	94,3	175,2	168,6	130,2	-40,6	-336,8	-15,5	-15,5	198,2	-264,9
	0,0	-29,0	-57,9	-72,6	-86,9	-116,1	-156,6	94,3	231,5	252,8	242,5	128,0	-112,3	-25,0	-25,0	239,9	-223,2
	0,0	238,8	334,3	328,3	286,7	95,5	-257,6	-177,5	-118,4	-104,0	-100,1	-109,1	-184,8	246,2	-322,3	88,5	-61,0
	0,0	202,6	261,8	237,6	177,8	-49,4	-453,1	-83,2	154,9	211,7	227,0	145,3	-128,8	217,4	-351,1	359,4	-253,2
	0,0	32,0	28,7	13,9	-9,3	-82,4	-205,3	74,0	202,7	204,8	165,0	-26,0	-409,3	39,1	-99,7	278,4	-334,3
	0,0	22,2	9,5	-10,1	-38,2	-121,1	-257,6	74,0	259,0	289,1	277,3	142,5	-184,8	29,5	-109,2	320,1	-292,6

Таблица 4

Схемы загружения	Изгибающие моменты, кНм
	МА	В крайних пролетах					МВ	В средних пролетах					МС
		М1	М2	М3	М4	М5		М6	М7	М8	М9	М10
Ординаты основной эпюры моментов при загружении по схемам 1+3	Перераспределение усилий за счет уменьшения опорного момента на опоре В (максимальное значение) на величину 0.3*453,1=135,9Кн·м
	0,0	202,6	261,8	237,6	177,8	-49,4	-453,1	-83,2	154,9	211,7	227,0	145,3	-128,8
Ординаты добавочной эпюры	0,0	27,2	54,4	68,0	81,6	108,7	135,9	108,7	81,6	68,0	54,4	27,2	0,0
Ординаты перераспределенной эпюры IIа	0,0	229,7	316,1	305,5	259,4	59,4	-317,2	25,5	236,4	279,7	281,3	172,5	-128,8
Ординаты основной эпюры моментов при загружении по схемам 1+4	Перераспределение усилий за счет уменьшения опорного момента на опоре С (максимальное значение) на величину ΔМС = МС,III-0,7·МB,II =409,3-317,2=92,1 Кн·м
	0,0	32,0	28,7	13,9	-9,3	-82,4	-205,3	74,0	202,7	204,8	165,0	-26,0	-409,3
Ординаты добавочной эпюры	0,0	0,0	0,0	0,0	0,0	0,0	0,0	18,4	36,8	46,1	55,3	73,7	92,1
Ординаты перераспределенной эпюры IIIа	0,0	32,0	28,7	13,9	-9,3	-82,4	-205,3	92,5	239,5	250,9	220,3	47,6	-317,2

В связи с перераспределением изгибающих моментов уточняем величину поперечных сил. Поперечные силы в опорных сечениях ригеля после перераспределения усилий по схемам 1 + 3 при Н/м;v= 71,8 Н/м; М_В= -317,2 кНм; М_С= -128,8 кНм

кН;

кН;

кН;

кН.

Поперечные силы в опорных сечениях ригеля после перераспределения усилий по схемам 1 + 4 при Н/м;v= 71,8 Н/м; М_В= - 205,3 кНм; М_С= - 317,2 кНм:

кН;

кН;

кН;

кН.

Значения расчетных усилий при всех возможных схемах загружения пролетов ригеля временной нагрузкой и с учетом перераспределения усилий для схем загружения IIа иIIIaприведены в табл.5.

Таблица 5

Схемы загружения	Изгибающие моменты, кНм													Поперечная сила, кН
	МА	В крайних пролетах					МВ	В средних пролетах					МС	QA		QВл	QВп	QСл
		М1	М2	М3	М4	М5		М6	М7	М8	М9	М10
	0,0	238,8	334,3	328,3	286,7	95,5	-257,6	-177,5	-118,4	-104,0	-100,1	-109,1	-184,8	246,2		-322,3	88,5	-61,0
	0,0	229,7	316,1	305,5	259,4	59,4	-317,2	25,5	236,4	279,7	281,3	172,5	-128,8		233,9	-334,6	334,1	-278,6
	0,0	32,0	28,7	13,9	-9,3	-82,4	-205,3	92,5	239,5	250,9	220,3	47,6	-317,2	36,8		-102,0	289,9	-322,8
	0,0	22,2	9,5	-10,1	-38,2	-121,1	-257,6	74,0	259,0	289,1	277,3	142,5	-184,8	29,5		-109,2	320,1	-292,6

Определение размеров поперечного сечения ригеля. Необходимую расчетную высоту сечения ригеля из бетона класса В15 при_b2= 1.0;R_b= 8.5 МПа;R_bt= 0,75 МПа определяем по максимальному перераспределенному изгибающему моменту у граней колонн с размерамиb_c=h_c= 40 см.

кНм;

кНм.

При ширине ригеля b= 300 мм;= 0,3 ирасчетная высота

мм.

Полная высота мм. Принимаемh= 650 мм,b= 300 мм. Тогда в пролетах для нижней арматуры, расположенной в 2 ряда по высоте ригелямм, на опорах и в пролетах для верхней арматуры расположенной в один ряд по высоте ригелямм.

Расчет продольной арматуры. В качестве продольной арматуры в ригеле используем арматуру периодического профиля класса А400 сR_s= 355 Мпа (см. табл. 2.6 Пособия к СП 52-101 – 2003). Рабочую арматуру располагаем в трех плоских сварных сетках. Нижние продольные стержни пролетных сеток определяем по максимальным значениям «положительных» моментов при загружении по схемамIиIV(табл. 5). Верхние продольные стержни на опорах определяем по максимальным значениям «отрицательных» моментов у граней колонн (см. определение размеров поперечного сечения ригеля). Расчет арматуры сведен в табл. 6.

Таблица 6

Расчетные сечения	Расчетное усилие М, кНм	Размеры сечения, мм		Расчетные характеристики		Продольная рабочая арматура класса А400 мм2		Фактическая несущая способность, кНм
		b	h0	α0=		По расчету Аs=	Принятая арматура As, мм2.
В нижней зоне крайних пролетов	334,3	300	595	0.37	0,49	2094	3  22+ 3  22 Asф = 2281	364,2
В верхней зоне над опорами В у грани колонны	250,4	300	615	0,26	0,307	1356	2  25 + 1  22 Asф = 1363	251,7
В нижней зоне средних пролетов	289,1	300	595	0,32	0,40	1710	3  20+ 3  20 Asф = 1885	318,7
В верхней зоне над опорами С у грани колонны	252,6	300	615	0,262	0, 31	1369	2  25 + 1  25 Asф = 1473	271,8

Расчет поперечной арматуры. Величина максимальных поперечных сил у грани стены на 380 мм и у граней колонн при ширине их 400 мм с учетом коэффициента надежности по ответственности 0,95:

кН;

кН;

кН;

кН.

При Q_min= = 229, 1кН >_b3R_btbh₀= 0,60,753000.595 = 80,3 кН поперечная арматура в ригеле должна ставиться по расчету.

Принимаем поперечную арматуру класса A400 сR_sw= 285 МПа. В каркасах у опоры A при продольных стержнях диаметром 22 мм поперечные стержни из условия технологии сварки принимаем диаметром 8 мм, и у опор В и С при диаметре стержней опорной арматуры 25 мм – диметром 8 мм.

Расчет ригеля на действие поперечных сил у опоры А.

Максимально допустимый шаг поперечных стержней у опор в соответствии при ; sh/2 = 350 мм;s300 мм.

Кроме того м

Принимаем шаг поперечных стержней в сетках s= 200 мм.

Расчет прочности по полосе между наклонными сечениями. Q<0,3R_btbh₀, где Q принимается на расстоянии не менее h₀ от опоры 0,3R_btbh₀=0,3*8.5*10³*0,3*0,595=455.2кН> Q=Q–qh₀=229,1–94,98*0,95*0.595=175,4 кН, т.е. прочность наклонной полосы на сжатие обеспечена.

Расчет прочности на действие поперечной силы по наклонному сечению

q_sw= кН/м

Так как q_sw= 215,2 кН/м >Н/мм.=119.5 кН/м.

Длина проекции невыгоднейшего наклонного сечения на продольную ось элемента с. При расчете элемента на действие равномерно распределенной нагрузки qзначение с принимают равным, а если при этом<или, следует принимать.

Так как , то

м, но не более 3h₀=3*0.595=1,785 м

Принимаем длину проекции невыгоднейшего наклонного сечения с=0,69.

Длину проекции наклонной трещины с₀принимают равным с, но не более 2h₀=0.595*2=1,19м. Принимаем длину проекции наклонной трещины с=с₀=0,69.

Тогда Q_sw=0.75*q_sw*c₀=0.75*161.5*0.69=83,6 кН

Поперечную силу, воспринимаемую бетоном, определяют по формуле , но не болееQ_b,max=2.5*R_bt*b*h₀=2.5*0.75*300*0.595=334.7 кН и не менееQ_bmin=0.5*R_bt*b*h₀=0.5*0.75*300*0.595=66.9 кН. ПринимаемQ_b=173,2 кН.

Расчет изгибаемых элементов по наклонному сечению производят из условия Q<Q_sw+Q_b, гдеQ–поперечная сила в наклонном сечении с длинной проекции с; при вертикальной нагрузке, приложенной к верхней грани элемента, значениеQпринимается в нормальном сечении, проходящем на расстоянии с от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длинной с.

Q=Q–gc= 229,1– 23,18*0.95*0.75= 212,6 кН.

При Q_sw+Q_b=83,6+173,2=256,8 кН>Q=212,6 кН, т.е. прочность наклонных сечений на приопорном участке у опоры А обеспечена при установке поперечной арматуры диаметром 8 мм класс А240 с шагом 200 мм на приопорных участках, равных четверти пролета у опор обеспечена.

Определение шага поперечной арматуры в средней части пролета. В средней части пролетаQ₁=Q–q*(l_кр-h_c)/4 = 316,6 – 94,98*(6.3-0.2)/4*0.95 = 179 кН.

Определяем поперечную силу, воспринимаемую бетоном.

=119.5 кН/м..

Длина невыгоднейшего наклонного сечения , но не более 3h₀=3*0.595=1,785 м. Принимаем длину проекции невыгоднейшего наклонного сечения с=1.15 м.

Поперечную силу, воспринимаемую бетоном, определяют по формуле , но не болееQ_b,max=2.5*R_bt*b*h₀=2.5*0.75*300*0.595=334.7 кН и не менееQ_bmin=0.5*R_bt*b*h₀=0.5*0.75*300*0.595=66.9 кН. ПринимаемQ_b=103.9 кН.

Q_b=103.9 кН <Q₁= 179 кН, т.е. поперечная сила не может быть воспринята только бетоном. Предусматриваем установку поперечной арматуры с шагом не болееКроме того шаг хомутов, учитываемых в расчетеШаг поперечных стержней принимаемs=300 мм.

>Длина проекции невыгоднейшего наклонного сечения на продольную ось элемента с. Так как,

, но не более 3h₀=3*0.595=1,785 м

Принимаем длину проекции невыгоднейшего наклонного сечения с=0,78.

Длину проекции наклонной трещины с₀принимают равным с, но не более 2h₀=0.595*2=1.19 м. Принимаем длину проекции наклонной трещины с=с₀=0,78

Тогда Q_sw=0.75*q_sw*c₀=0.75*143.5*0,78=83.9 кН

Поперечную силу, воспринимаемую бетоном, определяют по формуле , но не болееQ_b,max=2.5*R_bt*b*h₀=2.5*0.75*300*0.595=334.7 кН и не менееQ_bmin=0.5*R_bt*b*h₀=0.5*0.75*300*0.595=66.9 кН. ПринимаемQ_b=153.2 кН.

При Q_sw+Q_b=83.9+153.2=237.1 кН >Q₁=179 кН, т.е. прочность наклонных сечений у опоры В и С обеспечена при поперечных стержнях Ø8 мм класса А400 с шагомs=300 мм.

Расчет прочности по наклонному сечению на действие момента.

Если у грани крайней свободной опоры ригеля верхний ряд нижней арматуры (3Ø22 мм) не доводим до опоры, а у оставшегося нижнего ряда арматуры (3Ø22 мм) отсутствуют специальные анкера, необходимо произвести расчет прочности наклонных сечений на действие момента.

Расчет производим из условия M ≤ M_s + M_sw

Определим усилие N_s в ратянутой арматуре

где l_s - расстояние от конца арматуры до точки пересечения с ней наклонного сечения, 380-15=365 мм.

Площадь опирания ригеля на кирпичную стену A_sup=b*l_sup=0.3*0.38=0.114 м²

Опорная реакция на опоре А: F_sup=Q_max=229,1 кН

Средние напряжения в ригеле на опоре от опорной реакции

Так как 0,25<

Расчетное сопротивление сцепления арматуры с бетоном R_bond = η₁ η₂R_bt

η₁ - коэффициент, учитывающий влияние вида поверхности арматуры и принимаемый равным:

2,5 - для арматуры классов А300, А400, А500;

η₂ - коэффициент, учитывающий влияние диаметра арматуры и принимаемый равным:

1,0 - при диаметре d_s <32 мм.

Значение относительной длины анкеровки

принимается не менее 15.

Длина зоны анкеровки l_an=λ_and_s=39.4*22=866,8 кН, принимаем не менее 200.

Поскольку к растянутым стержням в пределах длины l_s приварены 6 вертикальных поперечных стержней диаметром 6 мм и один горизонтальный поперечный стержень, увеличим усилие на величину.

Принимая

, принимаемую не более =71,6 кН

принимаемую не более =163.6 кН

Отсюда

Определяем максимально допустимое значение при α=0,7

принимается не менее 15.

l_an=λ_and_s=36,8*22=809,6 кН, принимается не менее 200 мм.

<

Принимаем

Определим плечо внутренней пары сил

Момент, воспринимаемой продольной арматурой равен M_s = N_s·z_s=182,5*0,56=102,2 кН м

Определим длину проекции невыгоднейшего наклонного сечения

 

Момент M_sw при поперечной арматуре в виде хомутов, нормальных к продольной оси элемента, определяют по формуле M_sw =0,5 q_sw c²=0,5*215,2*0,75²=60,5 кН м

Момент в наклонном сечении определяем как момент в нормальном сечении, расположенном в конце наклонного сечения, т.е. на расстоянии хо от точки приложения опорной реакции равной х=l_sup/3+c=0.38/3+0,75=0.88 м.

M_s+ M_sw=102,2+60,5=162,7 кН м < ,

т.е. если верхний ряд нижней арматуры (3Ø22 мм) не доводим до опоры, а у оставшегося нижнего ряда арматуры (3Ø22 мм) отсутствуют специальные анкера, прочность наклонных сечений по изгибающему моменту не обеспечена.

Если не обрывать часть продольной арматуры нижней зоны в пролете со стороны опоры А, а довести ее до конца ригеля, то длина зоны анкеровки для арматуры 3Ø22 мм l_an=λ_and_s=39.4*22=866,8 кН, принимаем не менее 200.

С учетом поперечной арматуры

Определяем максимально допустимое значение α=0,7,l_an=λ_and_s=36,8*22=809,6 кН, принимается не менее 200 мм.

Принимаем

Определим плечо внутренней пары сил

Момент, воспринимаемой продольной арматурой равен

M_s = N_s·z_s=365*0,543=198,2 кН м

M_s+ M_sw=198,2+60,5=258,7 кН м > ,т .е. прочность наклонных сечений по изгибающему моменту обеспечена.

Таким образом, для обеспечения прочности наклонных сечений по изгибающему моменту необходимо всю продольную арматуру нижней зоны в крайнем пролете со стороны опоры А довести до конца ригеля.

Расчет ригеля на действие поперечных сил у опор В и С. Максимально допустимый шаг поперечных стержней у опор в соответствии при;sh/2 = 615/2=307,5 мм;s300 мм.

Кроме того м

Принимаем шаг поперечных стержней в сетках s= 150 мм.

Расчет прочности по полосе между наклонными сечениями. Q < 0,3R_btbh₀, где Q принимается на расстоянии не менее h₀ от опоры 0,3R_btbh₀=0,3*8,5*10³*0,3*0,615=470,5 кН > Q=Q–qh₀=316,6 – 94,98*0,95*0.615=261,1 кН, т.е. прочность наклонной полосы на сжатие обеспечена.

Расчет прочности на действие поперечной силы по наклонному сечению

q_sw= кН/м

Так как q_sw= 286,9 кН/м >Н/мм.=127,7 кН/м.

Длина проекции невыгоднейшего наклонного сечения на продольную ось элемента с. При расчете элемента на действие равномерно распределенной нагрузки qзначение с принимают равным, а если при этом<или, следует принимать

м, но не более 3h₀=3*0.615=1,845 м и не менее 0,615.

Принимаем длину проекции невыгоднейшего наклонного сечения с=0,64

Длину проекции наклонной трещины с₀принимают равным с, но не более 2h₀=0.615*2=1,23 м. Принимаем длину проекции наклонной трещины с=с₀=0,64.

Тогда Q_sw=0.75*q_sw*c₀=0.75*286,9*0,64=137.7 кН

Поперечную силу, воспринимаемую бетоном, определяют по формуле , но не болееQ_b,max=2.5*R_bt*b*h₀=2.5*0.75*300*0.615=345,9 кН и не менееQ_bmin=0.5*R_bt*b*h₀=0.5*0.75*300*0.615=69,2 кН. ПринимаемQ_b=199.5 кН.

Расчет изгибаемых элементов по наклонному сечению производят из условия Q<Q_sw+Q_b, гдеQ–поперечная сила в наклонном сечении с длинной проекции с; при вертикальной нагрузке, приложенной к верхней грани элемента, значениеQпринимается в нормальном сечении, проходящем на расстоянии с от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длинной с.

Q=Q–νc= 316,6– 71,8*0,95*0.64= 272,9 кН.

При Q_sw+Q_b=137.7+199.5=337.2 кН >Q=272,9 кН, т.е. прочность наклонных сечений на приопорном участке у опоры А обеспечена при установке поперечной арматуры диаметром 8 мм класс А240 с шагом 150 мм на приопорных участках, равных четверти пролета у опор обеспечена.

Определение шага поперечной арматуры в средней части пролета. В средней части пролетаQ₁=Q–q*(l_ср-h_c)/4 = 316,6– 94,98*(6.79-0,2)/4*0.95 = 167.9 кН.

Определяем поперечную силу, воспринимаемую бетоном.

=127,7 кН/м.

Длина невыгоднейшего наклонного сечения , но не более 3h₀=3*0.615=1,845. Принимаем длину проекции невыгоднейшего наклонного сечения с=1.2 м.

Поперечную силу, воспринимаемую бетоном, определяют по формуле , но не болееQ_b,max=2.5*R_bt*b*h₀=2.5*0.75*300*0.615=345,9 кН и не менееQ_bmin=0.5*R_bt*b*h₀=0.5*0.75*300*0.615=69,2 кН. ПринимаемQ_b=106.4 кН.

Q_b=106.4 кН <Q₁= 167,9 кН, т.е. поперечная сила не может быть воспринята только бетоном. Поэтому предусматриваем установку поперечной арматуры с шагом не болееКроме того шаг хомутов, учитываемых в расчетеШаг поперечных стержней принимаемs=300 мм.

>

хомуты учитываются в расчете и

Длина проекции невыгоднейшего наклонного сечения на продольную ось элемента с. Так как ,

, но не более 3h₀=3*0.615=1,845 м

Принимаем длину проекции невыгоднейшего наклонного сечения с=0,8.

Длину проекции наклонной трещины с₀принимают равным с, но не более 2h₀=0.615*2=1.23 м. Принимаем длину проекции наклонной трещины с=с₀=0,8.

Тогда Q_sw=0.75*q_sw*c₀=0.75*143.5*0.8=86.1 кН

Поперечную силу, воспринимаемую бетоном, определяют по формуле ,Q_b,max=2.5*R_bt*b*h₀=2.5*0.75*300*0.615=345,9 кН и не менееQ_bmin=0.5*R_bt*b*h₀=0.5*0.75*300*0.615=69,2 кН. ПринимаемQ_b=159.6 кН.

При Q_sw+Q_b=86.1+159.6=245.7 кН >Q₁=167,9 кН, т.е. прочность наклонных сечений у опоры В и С обеспечена при поперечных стержнях Ø8 мм класса А240 с шагомs=300 мм..

Определение мест обрыва стержней продольной арматуры. С целью экономии арматуры часть стержней пролетной арматуры разрешается обрывать, не доводя до опор. При сварных каркасах в балках шириной более 150 мм до опор доводят не менее двух стержней. Места обрыва стержней определяются расчетом в соответствии с эпюрами моментов при соответствующих схемах загружения ригеля временной нагрузкой.

Расстояние от опор до мест теоретического обрыва стержней разрешается определять графически по эпюрам моментов в масштабе при условии, что эпюры вычерчены не менее чем по пяти ординатам в каждом пролете с помощью лекала.

Из условия обеспечения надежной анкеровки обрываемые стержни должны быть заведены за место теоретического обрыва на величину

если

где Q– поперечная сила от расчетных нагрузок в месте теоретического обрыва стержней при соответствующей схеме загружения:d– диаметр обрываемых стержней;R_sw – расчетное сопротивление поперечной арматуры.

В средних пролетах ригеля в нижней зоне обрываем три стержня диаметром 18 мм, расположенных во втором ряду.

В верхней зоне у опоры В со стороны крайнего пролета обрываем сначала два стержня диаметром 25 мм, а затем – один стержень диаметром 22 мм, заменив их после обрыва стержнями диаметром 14 мм из стали класса А400. Соединение стержней диаметром 22 мм со стержнями диаметром 14 мм выполняется контактной стыковой или ванной сваркой по типу 5 или 7.

Таблица 7

Расположение стержней		Арматура в сечении, мм2			Расчетные характеристики
		До обрыва стержней As	обрываемая	После обрыва стержней As1	b, мм	h0, мм	bh0, мм2x x10-2			A0	M=Rbbh02A0, кНм
В нижней зоне ригеля	У опоры В	322+322 2281	322 1140	322 1140	300	615	1845	0,0062	0,26	0,226	218,0
	В среднем пролете: У опоры В	320+320 1885	320 942	320 942	300	615	1845	0,0051	0,21	0,188	181,3
	У опоры С	320+320 1885	320 942	320 942	300	615	1845	0,0051	0,21	0,188	181,3
В верхней зоне ригеля	У опоры В: со стороны крайнего пролета	225+122 1363	225 982 125 491	122+214 689 314 462	300	615	1845	0,0037 0,0025	0,155 0,104	0,133 0,10	128,3 96,5
	со стороны среднего пролета	225+125 1473	225 982	125+214 799	300	615	1845	0,0043	0,18	0,164	158,2
	У опоры С: со стороны обоих пролетов	225+125 1473	225 982	125+214 799	300	615	1845	0,0043	0,18	0,164	158,2

Таблица 8

Место расположения обрываемых стержней		Продольная арматура _________ Обрываемая арматура	Поперечная арматура Количество ________ Шаг мм2/мм	Поперечная сила в месте теоретического обрыва стержней, кН			Длина запуска обрабатываемых стержней за место теоретического обрыва, мм	Минимальное значение =15d или 200 мм	Принятая величина , мм	Расстояние от оси опоры, мм
										До места теоретического обрыва (в масштабе по эпюре материалов)			До фактического места обрыва
В нижней зоне ригеля	У опоры В	322+322 322	151(38) 150	140	0,22	0,32 <0.615	428	320	450	1900			1450
	В среднем пролете: У опоры В	320+320 320	151 (38) 150	140	0,29	0,24 <0.615	341	300	350	2000			1650
	У опоры С	320+320 320	151 (38) 150	150	0,29	0,26 <0.615	360	300	400	1400	1000
В верхней зоне ригеля	У опоры В: со стороны крайнего пролета	225+122 225 122	151 (38) 100	90 80	0,29	0,16 <0.615 0,13 <0.615	280 250	375 330	400 350	1300 1750	1700 2100
	со стороны среднего пролета	225+125 225	151 (38) 100	60	0,29	0,1 <0.615	228	375	400	1000	1400
	У опоры С: со стороны обоих пролетов	225+125 225	151 (38) 100	220	0,29	0,38 <0.615	504	375	500	850	1350