II. Проектирование сборного железобетонного перекрытия.

Разбивочные (осевые) размеры панелей определяются в зависимости от величины временной нагрузки и принимаются в пределах от 1,2 до 1,5 м по ширине и от 5,0 до 7,0 м – по длине.

Перекрытие следует проектировать с наименьшим числом типоразмеров элементов. С этой целью рекомендуется принимать все ребристые панели одинаковой ширины и длины, чтобы их можно было изготавливать в одних и тех же опалубочных формах.

При рекомендуемой длине панелей и поперечном расположении ригелей на заданной длине здания L= 32,4 м могут разместиться 6 панелей. Длина панелей с учетом заделки крайних панелей в стены на глубину 120 мм будет

l_п= мм.

При рекомендуемых пролетах ригеля от 5,0 до 7,0 м на заданной ширине здания В = 25,8 м принимаем 4 пролета. При ширине панели от 1,2 до 1,5 м принимаем в средних пролетах ригеля по 5 панелей, в крайних – по 4,5 панели.

Ширина панелей мм

С учетом допусков на изготовление 5 мм/пог.м но не более 30 мм на весь размер элемента и для образования швов замоноличивания между панелями принимаем конструктивные размеры панелей 13505410 мм

Во всех ребристых плитах при ширине их более 1,2 м предусматриваем устройство пяти поперечных ребер. В полках плит марок П-2 и П-3 устраиваются вырезы для пропуска колонн со смещением осей крайних поперечных ребер от торца плиты на 285 мм.

1. Расчет плиты п-1.

Расчет полки плиты. Полка плит марок П представляет собой четыре прямоугольные ячейки в плане со сложным характером опирания сторон. В поперечном направлении полка защемлена в продольных ребрах,а в продольном направлении она работает как неразрезная многопролетная конструкция, опорами которой являются поперечные ребра.

С целью упрощения расчета каждую из ячеек полки в статическом отношении условно рассматриваем как плиту, опертую по контуру, с частичным защемлениемв продольных и поперечных ребрах. За расчетные пролеты принимаются: в коротком направлении (пролет в свету) l₁=b_f – 2b₁= 1350 – 902 = 1170 мм; в длинном направленииl₂=l–b₂ = 1210 –85 = 1125 мм, гдеb₁иb₂– ширина поверху продольного и поперечного ребер соответственно. Соотношение сторон полки плиты,l₁= l₀

Нагрузка на полосу плиты с условной шириной 1,0 м при толщине плиты 50 мм , кН/м:

Нормативная	Расчетная
Постоянная:
от веса пола в виде цементной стяжки толщиной 20 мм с плотностью 20 кН/м3 200,02=0,4 от веса плиты 250,05=1,25 Всего постоянная gn=0,4+1,25=1,65 Временная vn=11 Полная 1,65+11=12.65 Постоянная и длительная 12,6-1,5=11.15	0,41,2=0,48 1,251,1=1,375 g=0,48+1,375=1,855 v=111,2=13,2 1,855+13,2=15,055

Изгибающий пролетный момент в полке плиты на 1 м ширины с целью упрощения расчета вычислим по формуле М = М₀= М₁= М₂=, допуская соотношение сторон равным 1 (фактически) и следовательно опорные моменты равными пролетным коэффициент= 0,8 учитывает благоприятное влияние распора в жестком контуре М =кНм =317566 Нмм,а от постоянных и длительных М₁=0,8*13,2*1,125²/48=0,278 кНм = 278438 Нмм.

Допускается, что М₁ = М₂ = - M_I = - M_I = - M_II =- M_II

М₁/М=278438/317566=0,88 < 0,9 расчетные сопротивления определяются с коэффициентом условий работы _b2 = 1.

Панель проектируем из бетона класса В20 с характеристиками: R_b = 11,5 МПа; R_bt = 0,9 МПа; R_{b ser} = 15,0 МПа; R_{bt ser} = 1,35 МПа; Е_b = 27500 МПа с учетом тепловой обработки бетона.

Вкачестве рабочей арматуры используем проволоку класса В500 с расчетным сопротивлениеR_s = 415 МПа, ; Е_s = 200000 МПа в плите в виде сварных рулонных сеток с продольной и поперечной рабочей арматурой, а в продольных и поперечных ребрах – стержневую арматуру класса А400 в виде плоских сварных каркасов с R_s = 355 МПа. Поперечную арматуру в ребрах панели принимаем класса А240 с R_sw = 170 МПа, Е_s = 200000 МПа.

Уточняем толщину плиты, приняв коэффициент армирования _s = 0,006:

;

мм;

мм.

Принимаем плиту толщиной 50 мм с h₀ = 50 – 15 = 35 мм.

Определим площадь сечения арматуры на 1 м ширины плиты при

мм².

Принимаем рулонную сетку С-1 маркис продольной и поперечной рабочей арматурой площадью А_s^ф=47 мм²; сетка С–1 раскатывается вдоль продольных ребер на всю ширину полки. Дополнительная сетка С – 4 заводится в продольные ребра на длину, равную .

Расчет промежуточного поперечного ребра.Поперечные ребра панели монолитного связаны с продольными ребрами, однако, учитывая возможность поворота их при действии внешней нагрузки, за расчетную схему поперечного ребра в запас прочности принимаем балку со свободным опиранием. Расчетный пролет поперечного ребра исчисляется как расстояние между осями продольных ребер:мм.

Принимаем высоту поперечных ребер 200 мм, ширину по низу – 60 мм, по верху – 85 мм.

Максимальная нагрузка на среднее поперечное ребро передается с треугольных грузовых площадей А_с= 0,5l₁². Треугольную нагрузку допускается заменить на эквивалентную равномерно распределенную по формуле;

кН/м,

где мм – средняя толщина поперечного ребра;

временная кН/м,

кН/м.

Суммарная равномерно распределенная нагрузка

кН/м.

Расчетные усилия кНм = 2,3810⁶Нмм;

кН.

В том случае, когда пролет , грузовая площадь имеет вид трапеции. Расчетные формулы преобразуется так:

;

кН/м;

;

.

При отношении толщины плиты к высоте ребра за расчетное сечение поперечного ребра принимаем тавровое с шириной полки в сжатой зоне

мммм.

Необходимое количество продольной арматуры класса А400 при мм.

= 0,018<т.е сжатая арматура по расчету не требуется.

мм²

Принимаем в поперечных ребрах плоские сварные каркасы с продольной арматурой из стержней диаметром 8 мм с А_s= 50.3 мм².

При Q= 7,6*0,95= 7,22 кН <Н =36,2 кН прочность полосы обеспечена.

При высоте ребра 20 см и продольной арматуре 8 мм принимаем поперечные стержни в каркасах из арматуры класса А240 диаметром 6 мм с шагоммм < 300 мм принимаем 75 мм.

Прочность наклонных сечений поперечных ребер при

Н/мм>Н/мм.=2.48*10⁶кН/м.

Длина проекции невыгоднейшего наклонного сечения на продольную ось элемента с. При расчете элемента на действие равномерно распределенной нагрузки qзначение с принимают равным, а если при этом<или, следует приниматьмм.

кН/м.

Так как

.

Тогда Q_sw=0.75*q_sw*c₀=0.75*66*210=10395 Н.

Поперечную силу, воспринимаемую бетоном, определяют по формуле ,

Q=Q_max–q₁c= 7,22– 6,85*0.21= 5,78 кН.

При Q_s+Q_b=10,4+11,8=22,2кН>Q=5,78 кН, т.е. прочность наклонных сечений обеспечена.

Проверим требование т.е требование выполнено.

Расчет продольного ребра. Высоту продольных ребер ориентировочно определяем из соотношений мм. Полученное значение высоты округляем в большую сторону с кратность 50 мм, но ограничиваем h  500 мм. Окончательно принимаем h = 400 мм. В качестве опорных конструкций для панелей принимаем ригели прямоугольного сечения с шириной ребра 25 см.

Нагрузка на два продольных ребра, кН/м:

Нормативная	Расчетная
Постоянная:
от веса пола 0,41,358=0,543 от веса плиты 1,2501,358=1,7 от веса поперечных ребер 50,5(0,085+0,06)(0,200,05)1,05255,44=0,262 от веса продольных ребер 20,08(0,400,05)25=1,4 gn=3,91 Временная vn =111,358=14,94	0,5431,2=0,652 1,71,1=1,87 0,2621,1=0,288 1,41,1=1,54 g=4,35 v=14,941,2=17,93

Полная нагрузка, Н/м:

нормативная qⁿ= 3,91+14,94=18,85,

расчетная q= 4,35+17,93=22,28,

в том числе кратковременно действующая часть нормативной нагрузки

;

длительно действующая нормативная нагрузка

За расчетную схему для продольных ребер принимаем однопролетную балку со свабодным опиранием концов на ригели, расчетный пролет определяется как расстояние между серединами площадок опирания ребер панели на ригели

мм = 5,32 м.

Усилия в двух продольных ребрах:

от расчетных нагрузок

кНм = 78,710⁶Нмм;

кН;

от нормативных нагрузок

кНм;

кН,

в том числе от кратковременной

кНм;

ДлительнойкН.

Расчетное сечение двух продольных ребер – тавровое с полкой в сжатой зоне.

Ширина полки, вводимая в расчет, при наличии поперечных ребер мм.

Расчетная высота сечения см. При ширине продольных ребер по верху 95 мм и по низу 75 мм суммарная толщина двух ребер в уровне центра тяжести арматуры без учета швов замоноличивания будет 170 мм.

Размеры сечения изгибаемых элементов должны обеспечивать прочность наклонных сечений на действие поперечной силы по наклонной полосе между возможными наклонными трещинами

Расчет прочности нормальных сечений. Поскольку , поэтому учитываем коэффициент условий работы 1,0.

Бетон класса В20 с характеристиками: R_b = 11,5 МПа; R_bt = 0,9 МПа; R_{b ser} = 15,0 МПа; R_{bt ser} = 1,35 МПа; Е_b = 27500 МПа с учетом тепловой обработки бетона.

Работу бетона в швах замоноличивания в запас прочности условно не учитываем, предполагая, что при неблагоприятных условиях надежная совместная работа бетона замоноличивания с продольными ребрами за счет их сцепления может быть не обеспечена. Тогда расчетная ширина полки мм.

При Нмм =260 кНм >М = 78,7 кНм, нейтральная ось проходит в пределах полки (х < h_f) и элемент рассчитывается как прямоугольный с шириной b_f = 1330 мм.

Необходимое количество продольной арматуры класса А400 при

, т.е сжатая арматура по расчету не требуется.

мм².

Принимаем стержневую арматуру из стержней 220А400 с А_s^ф = 628 мм² > 593 мм². Монтажную арматуру в каркасах продольных ребер принимаем класса А240 диаметром 10 мм.

Расчет прочности наклонных сечений продольных ребер.

При Н = 27.9 кН <Q = 59,2 кН поперечная арматура в продольных ребрах должна ставиться по расчету.

При продольной арматуре диаметром 20 мм принимаем поперечные стержни из арматуры класса A240 диаметром 6 мм.

Шаг поперечных стержней s в каркасах при высоте продольных ребер h = 40 см  45 см не должен превышать м;

Принимаем шаг поперечных стержней в каркасах s = 150 мм на приопорных участках и 300 мм на средних.

Расчет прочности по полосе между наклонными сечениями. Q < 0,3R_bbh₀, где Q принимается на расстоянии не менее h₀ от опоры 0,3R_bbh₀=0,3*11.5*10³*0,17*0,365=214.1 кН > Q=Q–qh₀=59,2– 22,28*0.365=51,1 кН, т.е. прочность наклонной полосы на сжатие обеспечена.

Расчет прочности на действие поперечной силы по наклонному сечению

q_sw= кН/м

Так как q_sw= 64,6 кН/м >Н/мм.=30,6 кН/м.

Длина проекции невыгоднейшего наклонного сечения на продольную ось элемента с. При расчете элемента на действие равномерно распределенной нагрузки qзначение с принимают равным, а если при этом<или, следует принимать.

Так как

, но не более 3h₀=3*0.365=1,095 м.

Принимаем длину проекции невыгоднейшего наклонного сечения с=1,03.

Длину проекции наклонной трещины с₀принимают равным с, но не более 2h₀=0.365*2=0,73 м. Принимаем длину проекции наклонной трещины с=с₀=0,73

Тогда Q_sw=0.75*q_sw*c₀=0.75*64,6*0.73=35,4 кН

Поперечную силу, воспринимаемую бетоном, определяют по формуле , но не болееQ_b,max=2.5*R_bt*b*h₀=2.5*0.9*170*0.365=139.6 кН и не менееQ_bmin=0.5*R_bt*b*h₀=0.5*0.9*170*0.365=27.9 кН. ПринимаемQ_b=41,5 кН.

Расчет изгибаемых элементов по наклонному сечению производят из условия Q<Q_sw+Q_b, гдеQ–поперечная сила в наклонном сечении с длинной проекции с; при вертикальной нагрузке, приложенной к верхней грани элемента, значениеQпринимается в нормальном сечении, проходящем на расстоянии с от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длинной с.

Q=Q–νc= 59,2– 17,93*0.73= 46,1 кН.

При Q_sw+Q_b=35,4+41.5=76.9 кН>Q=46,1 кН, т.е. прочность наклонных сечений обеспечена.

Поскольку продольная арматура ребер по концам приварена к закладным деталям, проверку наклонных сечений на действие момента не производим.

Расчет ширины раскрытия наклонных трещин.Расчет железобетонных элементов третьей категории трещиностойкости по второй группе предельных состояний производится на действие нормативных нагрузок с коэффициентом надежности по нагрузке γ_f=1.

Расчет производим по формуле

где _s1– коэффициент, учитывающий продолжительность действия нагрузки (при непродолжительном действии равен 1, при продолжительном – 1,4);_s2– коэффициент, учитывающий профиль поперечной арматуры (для гладкой арматуры равен 0,8, для арматуры периодического профиля – 0,5);, где- относительное расстояние между поперечными стержнями;- относительное значение диаметра поперечной арматуры.

Напряжения в поперечной арматуре _swопределяют, принимая, что поперечная сила, воспринимаемая бетоном, отвечает своему минимальному значениюQ_bmin=0.5*R_bt.ser*b*h₀, следовательно, поперечная сила, передаваемая на поперечную арматуру, составляетQ-Q_{b min}. При этом поперечную арматуру, воспринимающую эту силу, учитывают на дине проекции наклонного сечения с=h₀, т.е. равный ее минимальному значению.

Тогда , гдеA_sw– площадь сечения поперечной арматуры, расположенной в одной нормальной к продольной оси элемента плоскости, пересекающей наклонное сечение.

Вычисляем

Q_bmin=0,5*1,35*170*365=41884 Н

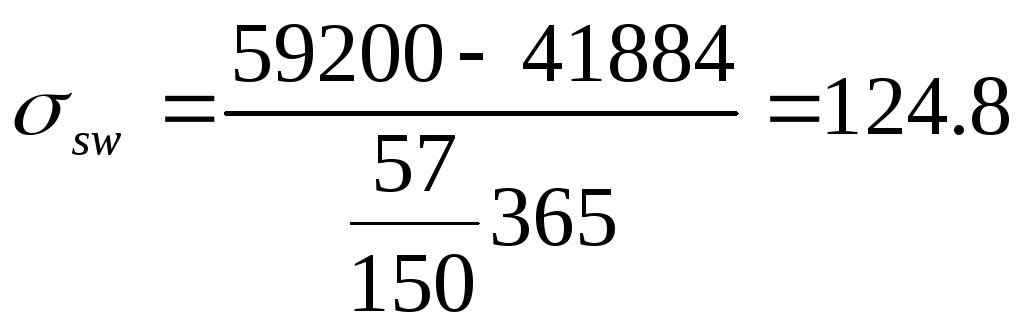МПа

т.е ширина раскрытия наклонных трещин меньше предельно допустимой величины.

Расчет ширины раскрытия нормальных трещин.

Определяем момент образования трещин . Для этого определяем геометрические характеристики приведенного сечения прииA_s'=0.

Площадь приведенного сечения A_red=A+ α*A_sp=bh+(b’_f-b)h’_f+A_s=170*400+(1330-170)50+7.27*628=130565,6 мм²

Расстояние от наиболее растянутого волокна бетона до центра тяжести приведенного сечения:

y_t=S_red/A_red=(68000*400/2+58000(400-50/2)+4565,6*35)/ 130565,6=272 мм

Момент инерции приведенного сечения относительно его центра тяжести:

Y_red=bh³/12+bh(y_t-h/2)² + (b_f’-b)h’_f³/12 + (b’_f-b)h’_f(h-h’_f/2-y_t)² +A_s(yt-a)²=

=170*400³/12+170*400(279-200)²+1160*50³/12+1160*50(400-25-279)²+7.27*628*(279-35)²=2,15*10⁹мм⁴

Момент сопротивления приведенного сечения:

W=Y_red/y_t=2,15*10⁹/279=7,7*10⁶мм³

Учтем неупругие деформации растянутого бетона путем умноженияWна коэффициент γ, равный 1, 3W_pl=7,7*10⁶*1.3=10,0*10⁶, тогда изгибающий момент при образовании трещин с учетом неупругих деформаций

Определим напряжения в арматуре

Рабочая высота сечения h₀=400-35=365 мм; коэффициент приведения. Тогда приии плечо внутренней пары силz_s=ςh₀=0.9*365=328,5 мм.

Вычисляем

Определим расстояние между трещинами l_s. Поскольку высота растянутого бетона, равная при к=0,9 (для таврового сечения)y=y_tk=279*0.9=251,1 мм >h/2=200 мм, площадь сечения растянутого бетона принимаем равнойA_bt=b*0.5*h=170*200=34000 мм².

Тогда , что больше 400 мм, поэтому принимаемl_s=400 мм.

Значение ψ_sопределяем по формуле

Определим ширину продолжительного раскрытия трещин, принимая ₁=1,4,₂=0,5,₃=1.

, что меньше допустимой величины 0,3 мм.

Определение прогиба ребристой панели. Определим кривизну в середине пролета от действия постоянных и длительных нагрузок, так как прогиб ограничивается эстетическими требованиями.

Момент в середине пролета равен γ_nM_max=0.95*59,4=56,4 кН

Коэффициент армирования при h₀=365 мм равен

При продолжительном действии нагрузки и нормальной влажности коэффициент приведения арматуры равен .

При и₁=0,56, а при α_s1=20, μα_s1=0.015*20=0.3, μ’_f=0,85 μ_f=0,₂=0,293.

Определим прогиб, принимая S=5/48:

Согласно СНиП 2.01.07-85* предельно допустимый прогиб по эстетическим требованиям для пролета 5,32 м равен 26,6 мм > 14,4 мм, т.е. условие выполняется.