Натуральные логарифмы

Натуральные логарифмы — это логарифмы по основанию е, где — иррациональное число. Обозначаются .

Основное свойство функции «натуральный логарифм» состоит в том, что касательная к графику функции в его точке наклонена к оси OX под углом 45 (рис. 67). Соответствующая этой функции обратная функция называется экспонентой. Графики обеих взаимно обратных функций и приведены на рис. 68.

Рис. 67

Рис. 68

5. Тригонометрические функции

Основными тригонометрическими функциями называются следующие четыре функции: , , , . Их графики приведены на рис. 69.

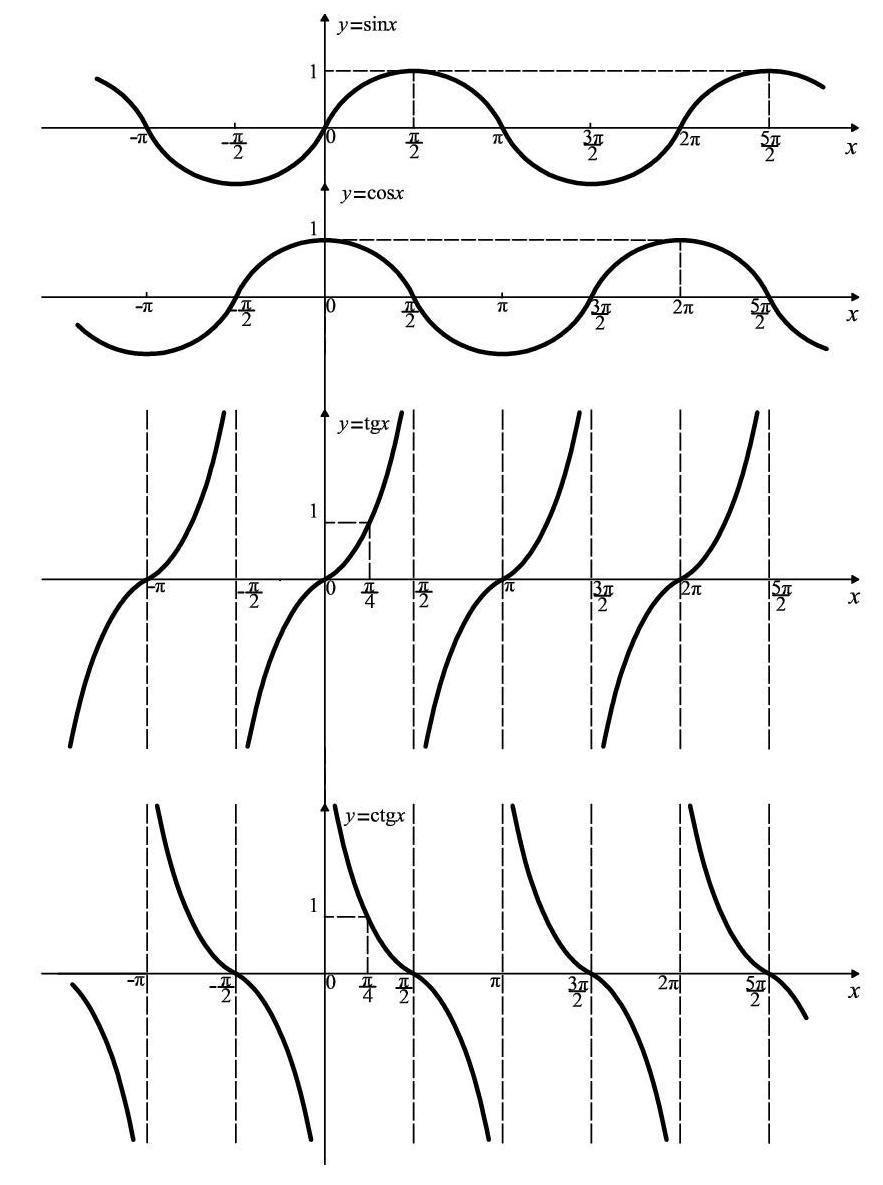
Рис. 69

Для определения основных тригонометрических функций используется тригонометрический круг (рис. 70).

Рис. 70

ООФ: , ; , ; ,; , . ОЗФ: ; ; ; .

Основным отличительным свойством тригонометрических функций является их периодичность:

• для и – наименьший период ;

• для 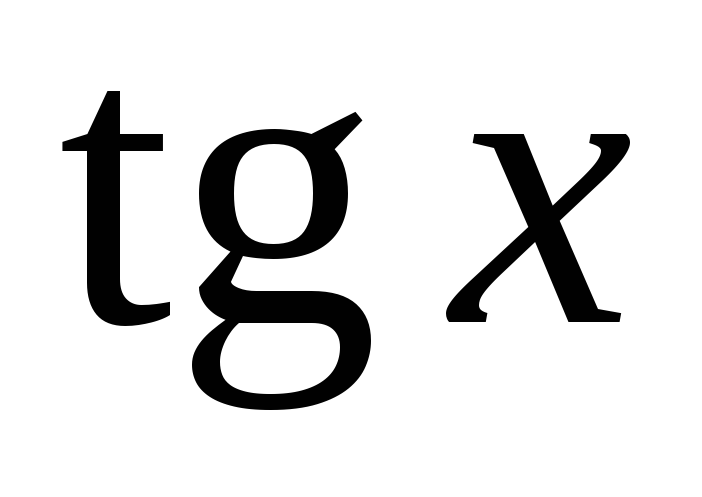и — наименьший период .

Основные формулы, связывающие тригонометрические функции

1. Для функций одного аргумента:

2. Для функций аргумента кратности 2:

3. Для функций существенно различных аргументов

; ;

6. Обратные тригонометрические функции

Обратные тригонометричекие функции , , , определяются на основных промежутках строгой монотонности «прямых» тригонометрических функций: , , , .

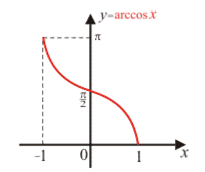
Ниже приведены определения этих функций и их графики (рис. 71-74).

(Сформулируйте определения и постройте графики обратных тригонометрических функций.)

Рис. 71	(арккосинус х)– это есть главный угол, косинус которого равен х; он берется в I или во II четверти, поэтому ООФ: , ОЗФ: ; при этом .
Рис. 72	(арксинус х) — это есть главный угол, синус которого равен х; он берется в I или в IV четверти, поэтому ООФ: , ОЗФ: ; при этом .
Рис. 73	(арктангенс х)– это есть главный угол, тангенс которого равен х; он берется в I или в IV четверти, поэтому ООФ: , ОЗФ: ; при этом .
Рис. 74	(арккотангенс х)– это есть главный угол, котангенс которого равен х; он берется в I или во II четверти, поэтому ООФ: , ОЗФ: ; при этом .

Через обратные тригонометрические функции записываются формулы для решенияя простейших тригонометрических уравнений:

7. Гиперболические функции

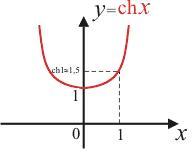
Гиперболические функции определяются через показательную функцию по основанию е (через экспоненту) и обозначаются y = shx, y = chx, y = thx, y = cthx. Ниже на рисунках 75-78 приведены их определения, графики и основные свойства.

1. Гиперболический синус	2. Гиперболический косинус
Рис. 75	Рис. 76
ООФ: , ОЗФ: , функция нечетная,	ООФ: , ОЗФ: , функция четная,
3. Гиперболический тангенс	4. Гиперболический котангенс
Рис. 77	Рис. 78
ООФ: , ОЗФ: , функция нечетная,	ООФ: , ОЗФ: , функция нечетная

О

сновное тождество для гиперболических функций:

Доказательство проводится на основании определения гиперболических функций:

. 