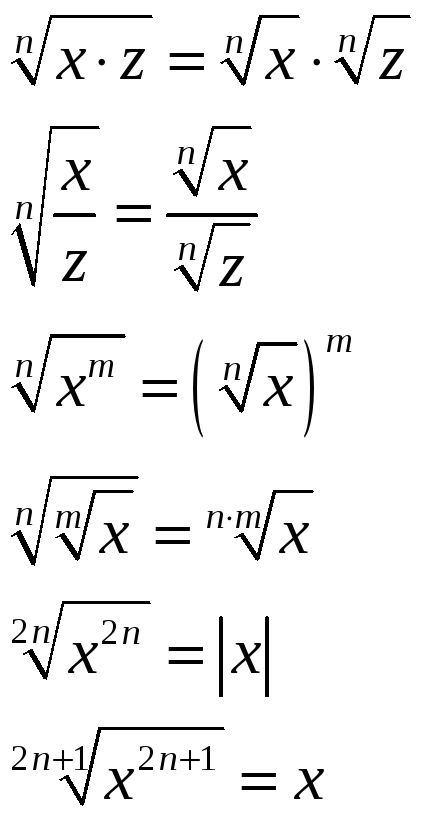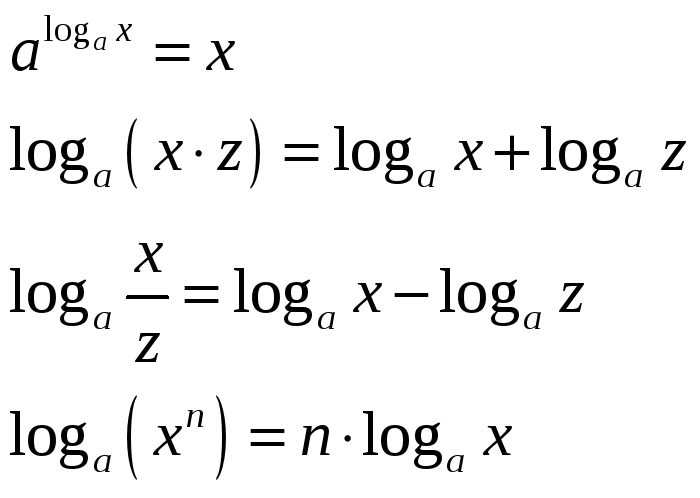145

11. Основные элементарные функции, их определения и графики. Преобразования графиков Содержание

§ 11. Основные элементарные функции, их определения и графики. Преобразования графиков 129

11.1. Список основных элементарных функций 129

11.2. Степенная функция 130

11.3. Показательная функция 131

11.4. Логарифмическая функция 132

11.5. Тригонометрические функции 134

11.6. Обратные тригонометрические функции 138

11.7. Гиперболические функции 139

11.8. Основные преобразования графиков 141

11.9. Упражнения для самостоятельной работы 141

Вопросы для самопроверки 144

Глоссарий 144

1. Список основных элементарных функций

Как было определено в предыдущем параграфе, к основным элементарным функциям относятся следующие функции:

• постоянная функция y = сonst, ;

• степенная функция , где ;

• показательная функция , где a > 0, a  1;

• логарифмическая функция , где a > 0, a  1;

• тригонометрические функции , , , ;

• обратные тригонометрические функции , , , ;

• гиперболические функции y = sh x, y = ch x, y = th x, y = cth x .

Основные свойства большинства этих функций считаются известными, они изучаются в средней школе и хорошо прочитываются по графикам этих функций. Здесь приведены определения и графики основных элементарных функций, а также основные формулы, которые необходимо знать для преобразования выражений, содержащих эти функции.

2. Степенная функция

Степенной функцией аргумента х называется функция , где . Ниже приведены определения основных степеней величины х и графики соответствующих степенных функций (рис. 61-64).

1. Если , то	Рис. 61
2. Если , то ; если , то	Рис. 62
3. Определение степени с отрицательным показателем: , где	Рис. 63
4. Определение степени с дробным показателем: ,	Рис. 64

Определение степенной функции с любыми рациональными или иррациональными показателями можно найти в дополнительной литературе.

Основные формулы преобразования степеней и корней

Напомним, что записанные равенства справедливы только на общей части ОДЗ для буквенных величин, входящих в выражения, стоящие в левой и в правой частях каждого равенства.

3. Показательная функция

Показательной функцией аргумента х называется функция вида

, где a > 0, a  1

Графики показательных функций различаются по условиям a > 1 или 0 < a < 1 (рис. 65).

Рис. 65

ООФ: ОЗФ:

4. Логарифмическая функция

Логарифмической называется функция вида , где a > 0, a  1. Напомним, что логарифмом числа х по основанию а называется такой показатель степени у, что , то есть .

Из определения логарифма следует, что логарифмическая и функции являются взаимно обратными. Графики логарифмических функций различаются, как и графики показательных функций по условиям a > 1 или 0 < a < 1 (рис. 66)

Рис. 66

ООФ: ОЗФ:

Основные формулы преобразования логарифмов

При использовании этих формул необходимо помнить о требовании совпадения ОДЗ для выражений, стоящих в левой и в правой частях каждого равенства.