
- •Целые функции (многочлены) и их основные свойства. Решение алгебраических уравнений на множестве комплексных чисел Содержание
- •§ 13. Целые функции (многочлены) и их основные свойства. Решение алгебраических уравнений на множестве комплексных чисел 165
- •Основные определения
- •Основные свойствацелых многочленов
- •Основные свойства корней алгебраического уравнения
- •Решение основных алгебраических уравнений на множестве комплексных чисел
- •Алгебраические уравнения первой степени:
- •Квадратные уравнения:
- •Двучленные уравнения степени n:
- •Упражнения для самостоятельной работы
- •Вопросы для самопроверки
- •Глоссарий
Решение основных алгебраических уравнений на множестве комплексных чисел
Алгебраические уравнения первой степени:
![]()
![]()
![]() ,
,![]()
![]()
![]() – единственный простой корень.
– единственный простой корень.
Например,
![]()
![]()
![]() .
.
Квадратные уравнения:
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
квадратное уравнение всегда имеет два корня (различных или равных).
Нетрудно
показать, что для корней
![]() квадратного уравнения всегда справедливатеорема
Виета:
квадратного уравнения всегда справедливатеорема
Виета:
![]() ,
,![]()
![]()
![]()
Примеры (решение квадратных уравнений)


 ;
;
проверка
по теореме Виета:
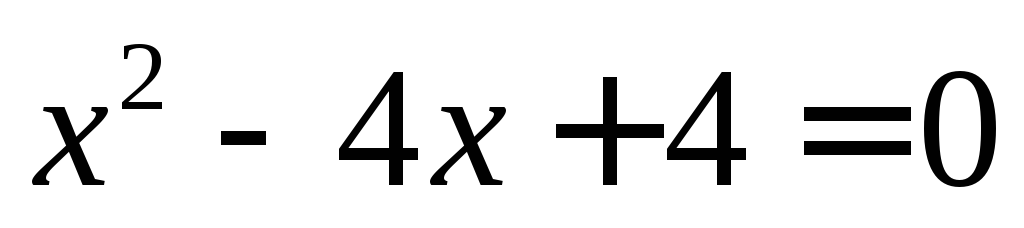



 ;
;



 ,
,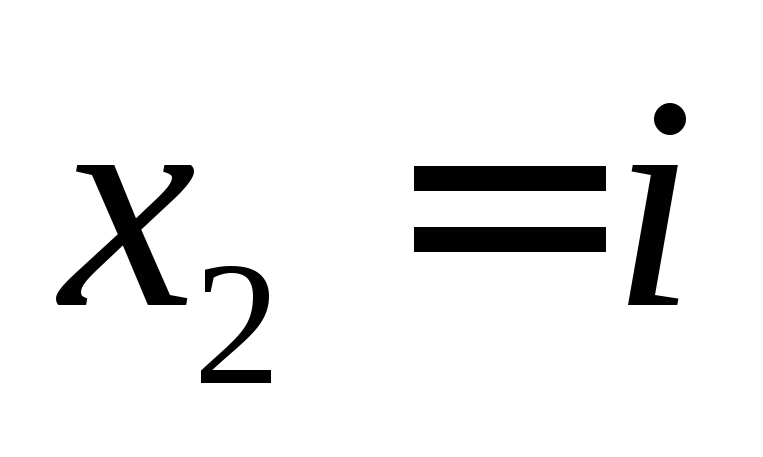 ;
;
проверка
по теореме Виета:
Двучленные уравнения степени n:
![]() ,
,![]()
![]()
![]()
![]()
двучленное уравнение степени nвсегда имеетnразличных корней.
Пример (решение двучленного уравнения)
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() ,
,
![]() .
.
Алгебраические
уравнения
![]() степени
степени
![]() ,
не являющиеся двучленными решаются
способом разложения многочлена
,
не являющиеся двучленными решаются
способом разложения многочлена![]() на множители, используя для этого в том
числе и теорему Безу.
на множители, используя для этого в том
числе и теорему Безу.
Пример (решение кубического уравнения)
Решим
кубическое уравнение:
![]() .
.
Решение
Это
уравнение третьей степени
![]() имеет три корня (действительные или
комплексные), при этом нужно считать
каждый корень столько раз, какова его
кратность. Так как все коэффициенты
данного уравнения являются действительными
числами, то комплексные корни уравнения,
если они есть, будут парными комплексно
сопряженными.
имеет три корня (действительные или
комплексные), при этом нужно считать
каждый корень столько раз, какова его
кратность. Так как все коэффициенты
данного уравнения являются действительными
числами, то комплексные корни уравнения,
если они есть, будут парными комплексно
сопряженными.
Подбором
находим первый корень уравнения
![]() ,
так как
,
так как![]() .
.
По
следствию из теоремы Безу имеем, что
![]() ;
выполняем это деление «в столбик»:
;
выполняем это деление «в столбик»:
-
_




_


_



Представляя
теперь многочлен
![]() в виде произведения линейного и
квадратичного множителя, получим:
в виде произведения линейного и
квадратичного множителя, получим:
![]()
![]()
![]() .
.
Другие корни находим как корни квадратного уравнения:
![]()
![]()
![]() .
.
Ответ:
![]() ,
,![]() .
.
Интересной на множестве комплексных чисел является обратная задача о составлении алгебраического уравнения по известным его корням.
Пример (составление алгебраического уравнения по его корням)
Составим алгебраическое уравнение наименьшей степени с действительными коэффициентами, если известно, что числа x1 = 3 иx2 = 1 + iявляются его корнями, причемx1является двукратным корнем, аx2— простым корнем.
Решение
Число
![]() тоже является корнем уравнения, так как
коэффициенты искомого уравнения должны
быть действительными. Поэтому искомое
уравнение всего имеет 4 корня:x1,
x1,
x2,
тоже является корнем уравнения, так как
коэффициенты искомого уравнения должны
быть действительными. Поэтому искомое
уравнение всего имеет 4 корня:x1,
x1,
x2,
![]() ,
следовательно его степень равна четырем.
,
следовательно его степень равна четырем.
Составляем
многочлен 4-й степени с корнями x1,
x1,
x2,
![]() по формуле (6):
по формуле (6):
![]()
![]()
![]()
![]()
Ответ:
![]() .
.
Упражнения для самостоятельной работы
1.Решите следующие квадратные уравнения относительно неизвестрнойхи сделайте проверку по теореме Виета:
1)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 4)
; 4)![]() ;
;
5)
![]() ; 6)
; 6)![]() .
.
2.Решите следующие двучленные уравнения на множестве комплексных чисел:
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() 4)
4)![]() .
.
3.Найдите все корни следующих алгебраических уравнений на множестве комплексных чисел:
1)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 4)
; 4)![]() ;
;
5)
![]() ; 6)
; 6)![]() .
.
4. Составьте алгебраические уравнения наименьшей степени с действительными коэффициентами, корнями которого являются заданные числа:
1)
![]() 2)
2)![]()
3)
![]()
4)
![]()
Ответы к упражнениям для самостоятельной работы
1.1)![]() ; 2)
; 2) ; 3)
; 3)![]() ;
;
4)
![]() ; 5)
; 5)![]() 6)
6)![]() .
.
2.1)![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)

 .
.
3.1)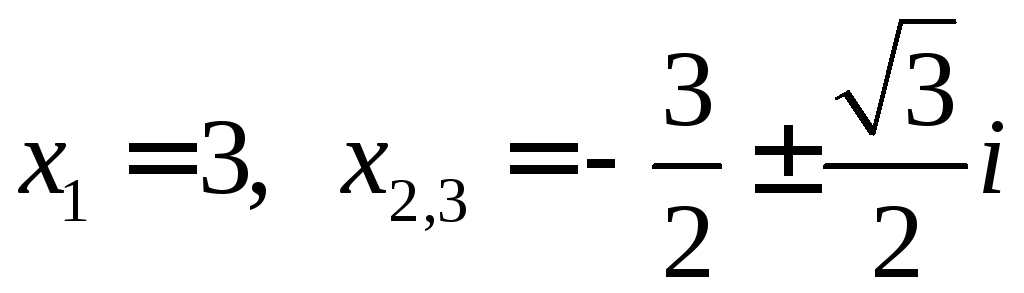 ; 2)
; 2)![]() ;
;
3)
![]() ; 4)
; 4)![]() ;
;
5)
 ;
;
6)
 .
.
4.1)![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 3)
; 3)![]() ;
;
