23

2. Множество действительных чисел: определение, геометрическая интерпретация, модуль, стандартные подмножества Содержание

§ 2. Множество действительных чисел: определение, геометрическая интерпретация, модуль, стандартные подмножества 19

2.1. Аксиоматическое определение множества действительных чисел 19

2.2. Модуль действительного числа 22

2.3. Стандартные подмножества множества действительных чисел 22

2.4. Примеры работы на множестве 18

2.5. Дискретные и непрерывные множества 19

2.6. Упражнения для самостоятельной работы 20

Вопросы для самопроверки 23

Глоссарий 24

1. Аксиоматическое определение множества действительных чисел

Множеством действительных чисел называется множество, содержащее более одного элемента и удовлетворяющее следующим свойствамI‑V.

I. Для определено единственное числоa + b, называемое суммой двух действительных чисел, так что выполняются условия:

1) a + b = b + a – свойство коммутативности операции сложения;

2) a + b + c = (a + b) + c — свойство ассоциативности операции сложения;

3)  число ноль такое, чтоa + 0 = a для 0 – этонейтральный элемент операции сложения;

4) для  противоположное число такое, что a + (–a) = 0;

5) число a + (–b) = a – b называется разностью чисел a и b.

II. Для определено единственное числоa·b (или ab), называемое произведением двух действительных чисел, так что выполняются условия:

1) a·b = b·a – свойство коммутативности операции умножения;

2) a·b·c = (a·b)·c – свойство ассоциативности операции умножения;

3)  число единица такое, чтоa·1 = a для 1 – этонейтральный элемент операции умножения;

4) дляединственное обратное числотакое, что;

5) число (илиa : b) называется частным от деления числа a на число b.

III. Имеет место свойство дистрибутивности произведения относительно суммы:

(a + b)·c = a·c + b·c для.

IV. Упорядоченность множества действительных чисел .

Дляимеет место одно и только одно отношение порядка:

a < b или a = b или a > b. При этом выполняются условия:

1) если a < b и b < c, то a < c — транзитивность;

2) если a < b, то a + c < b + c для ;

3) если a < b и c > 0, то a·c < b·c.

Как следствие этих условий получается свойство плотности множества действительных чисел :

Для иa < b  число .

 такое, что a < c < b 

Отношения порядка называются неравенствами или сравнениями действительных чисел.

Нестрогие неравенства:

V. Непрерывность множества действительных чисел :

Для  непустых множеств и, у которых дляивыполняется неравенство, существует такое число, что выполняется соотношениедляи для(рис. 12).

Рис. 12

Перечисленные свойства I-V определяют множество в том смысле, что из этих свойств следуют все остальные его свойства. Поэтому набор свойств I-V и даёт аксиоматическое определение множества.

Геометрическая интерпретация множества

Геометрическая интерпретация множества проводится на координатной (числовой) прямой, то есть на прямой с указанным на ней направлением, началом отсчета и масштабной единицей (рис. 13).

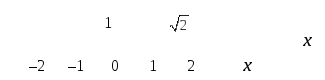
Рис. 13

Смысл этой интерпретации состоит в том, что любому числу ставится во взаимно однозначное соответствие точка с координатойxна числовой прямой.

2. Модуль действительного числа

 Определение модуля действительного числа:

 Геометрический смысл модуля действительного числа: — это расстояние от точкиxдо точки 0 на координатной прямой (рис. 14).
 Геометрический смысл модуля разности двух действительных чисел: геометрически означает расстояние между точкамиxиx0на координатной прямой (рис. 15).
Рис. 14	Рис. 15

 Основные свойства модуля действительного числа:

1)

2) ;

3) — неравенство треугольника;

4)