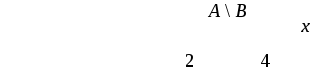5. Примеры выполнения операций над множествами

Пример 1 (выполнение операций над конечными множествами)

Даны два конечных числовых множества А иВ. Изобразить эти множества диаграммой Эйлера-Венна. Записать элементы множеств,,,,,.

а) ,; б),.

Решение

а) Так как множества А иВ имеют общие элементы, то для них диаграмма Эйлера-Венна имеет такой вид, как на рис. 10. Выполняем операции над множествами по их определениям:

Рис. 10

; ;;;

б) Множества А иВ не содержат одинаковых элементов, отображаем это диаграммой Эйлера-Венна так, как на рис. 11.

Рис. 11

Записываем результаты выполнения операций над множествами AиB:

; ;;;

; .

Пример 2 (выполнение операций над бесконечными множествами)

Даны два бесконечных числовых множества и.

Записать промежутками множества A,B,,,,и изобразить эти множества геометрически на координатной прямойOX.

Множества иописать и построить на координатной плоскостиXOY.

Решение

Находим множества А иВ и изображаем их элементы на координатной оси:

.

.

Для выполнения операций объединения, пересечения и разности множеств удобно множества А иВ изобразить на одной координатной прямой (можно и кругами Эйлера):

Теперь выполняем операции над множествами, пользуясь определениями этих операций:

	;
	;
	;
	.
Множества иописываем по определению декартова произведения множеств и строим на координатной плоскостиXOY:

Пример 3 (определение элементов множества)

Записать элементы следующих множеств ,.

Решение

.

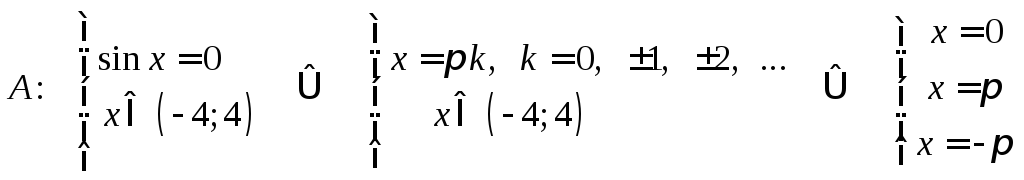
Ответ: , .

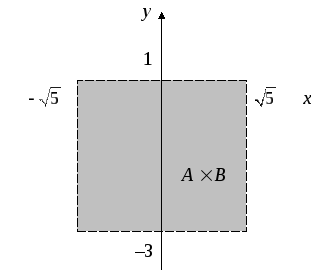
Пример 4 (множества точек на координатной плоскости)

Построить элементы множества на координатной плоскостиXOY.

Решение

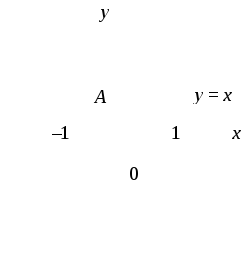
—это множество точек в полосе между прямыми x= –1 иx= 1, включающее в себя и точки на самих прямых;

—это множество точек, расположенных выше прямой y=x; оно включает в себя и точки на самой прямой;

пересечением множеств A₁иA₂определяем искомое множествоA.

Пример 5 (разбиение множества на подмножества)

Дано множество Анатуральных чисел от 10 до 25 включительно. Разбить множествоАна подмножества по принципу деления его элементов на числа 3 и 2.

Решение

Записываем множество Асписком его элементов:

.

По признаку деления чисел а на числа 3 и 2 определяются следующие четыре непересекающиеся подмножества:

—множество чисел а, которые делятся на число 3, но не делятся на число 2;

—множество чисел а, которые делятся на число 2, но не делятся на число 3;

—множество чисел а, которые делятся и на число 3, и на число 2, т.е делятся на число 6;

—множество чисел а, которые не делятся ни на число 3, ни на число 2.

Очевидно, что множества ,,,не пересекаются и их объединением получится данное множествоА:

Теперь распределяем числа апо множествам,,,:

,

,

,

.

6. Упражнения для самостоятельной работы

1.Дано, что. Записать промежутками и построить геометрически на координатной прямой множестваА,B,,,,. Описать и построить на координатной плоскости множестваи.

2.Дано, что. Записать и построить геометрически на координатной прямой множестваА,B,.

3.Определить элементы следующих множеств,,,,,.

4.Построить множества точек на координатной плоскостиXOY ,.

5.Дано множество.

Составьте разбиение множества Ана подмножества по признаку делимости его элементов на числа 2 и 5.

6.Дано: множество;

условие (1): х– неположительное число, большее чем -0.5;

условие (2): х– удовлетворяет неравенству.

Составьте разбиение множества Хна подмножества по признаку удовлетворения его элементов условиям (1) и (2). Сделайте иллюстрацию к разбиению с помощью диаграммы Эйлера-Венна и на координатной прямой.

Ответы к упражнениям для самостоятельной работы

1.;; ; ; ;;
;				.
2..
3. ,;,; , .
4.
5.,,,.
6.
		- множество х, удовлетворяющих условию (2) и не удовлетворяющих условию (1);
		- множество х, удовлетворяющих обоим условиям (1) и (2);
		- множество х, не удовлетворяющих ни условию (1), ни условию (2).