4. Корень натуральной степени из комплексного числа

Корнем степени n из комплексного числаz,где ,называется комплексное число , такое что

.

Например,

1. , так как ;

2. , так как ;

3. или , так каки.

Из определения очевидно следует, что операция извлечения корня из комплексного числа является многозначной.

Если использовать формулу Муавра, то нетрудно доказать следующее утверждение.

Теорема о значениях корня из комплексного числа

Корень натуральной степени nсуществует для любого комплексного числаzи еслиz0, тоимеетnразличных значений, вычисляемых по формуле Извлечение корня натуральной степени из комплексного числа(8) где ,— значение арифметического кореня на.

Геометрически, все значения расположены регулярным образом на окружности радиусомс начальным угломи углом регулярности.

Примеры (вычисление корня из комплексных чисел)

1) ,k = 0, 1, 2 

, ,.

2)

,

,.

Нетрудно показать, что корень квадратный существует на множестве комплексных чисел для любыхи имеет два противоположных значения при:.

5. Показательная форма комплексного числа

Показательной формой комплексного числа называется формула

Показательная форма комплексного числа, где. (9)

При этом аргумент обычно записывается в радианах.

Например,

1) ;

2) ;

3) ;

4) ,так как.

Действия над комплексными числами в показательной формевыполняются по правилам действий со степенями:

, , , ,.

(10)

Примеры (выполнение действий над компл. числами в показател. форме)

Пусть ,

.

Тогда ;

;

;

,

числа являются вершинами правильного пятиугольника, вписанного в окружность радиуса.

6. Формулы Эйлера

Используем определение (9) экспоненты с чисто мнимым показателем:

 ,

так как ,.

Из этих равенств следуютформулы Эйлера

(11) Формулы Эйлера

по которым тригонометрические функции идействительной переменнойвыражаются через показательную функцию (экспоненту) с чисто мнимым показателем.

7. Упражнения для самостоятельной работы

1.Вычислите степени числаi:

1)

2)

3)

4) .

2.Выполните действия над комплексными числами в алгебраической форме:

1) ; 2); 3);

4) ; 5); 6).

3. 1) Даны два комплексных числаОпределите, при каких действительных значенияххиyчислаибудут комплексно сопряженными.

2) Найдите множество комплексных чисел, каждое из которых равно квадрату сопряженного с ним числа.

4.Запишите каждое из следующих комплексных чисел в тригонометрической и в показательной формах:

1),

;

2)

.

5.Выполните действия над комплексными числами в тригонометрической или в показательной формах; ответ запишите в алгебраической форме:

1); 2); 3);

4); 5); 6);

7); ; 8); 9).

6.Постройте множества точек на комплексной плоскости:

7.. Докажите, что.

8.Найдите следующие множества:

Ответы к упражнениям для самостоятельной работы

1.1)

2)

3)

4)

2.1); 2); 3);

4); 5); 6).

3.1);

2)

4.1);

;

;

;

;

;

;

;

;

2);

;

;

;

;

;

;

;

.

5. 1); 2); 3); 4);

5)

6); 7) ; 8);

9).

6.

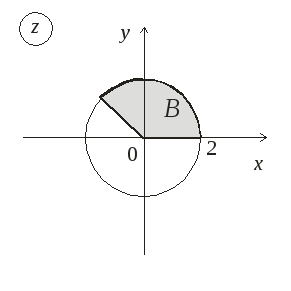
7.

8. ;

.