163

12. Комплексные числа: определения, геометрическая интерпритация, действия в алгебраической, тригонометрической и показательной формах Содержание

§ 12. Комплексные числа: определения, геометрическая интерпритация, действия в алгебраической, тригонометрической и показательной формах 145

12.1. Основные определения и геометрические трактовки 145

12.2. Модуль, аргумент и тригонометрическая форма комплексного числа 147

12.3. Арифметические действия над комплексными числами 149

12.4. Корень натуральной степени из комплексного числа 152

12.5. Показательная форма комплексного числа 154

12.6. Формулы Эйлера 155

12.7. Упражнения для самостоятельной работы 156

Вопросы для самопроверки 162

Глоссарий 162

1. Основные определения и геометрические трактовки

Комплексным числом zназывается выражение следующего вида

гдеx, y ,i— этомнимая единица, определяемая равенством.

Основные термины:

x = Re z—действительная часть комплексного числа z;y = Im z —мнимая часть комплексного числа z;—комплексно сопряженное числочислу z;—противоположное числочислу z;—комплексный ноль;

– так обозначаетсямножество комплексных чисел.

Примеры (комплексные числа)

1) z = 1 + i  Re z = 1, Im z = 1,  = 1 – i,  = –1 – i;

2) z = –1 + i  Re z = –1, Im z = ,  = –1 – i,  = –1 –i;

3) z = 5 + 0i = 5  Re z = 5, Im z = 0,  = 5 – 0i = 5,  = –5 – 0i = –5  если Im z = 0, то z = x — действительное число;

4) z = 0 + 3i = 3i  Re z = 0, Im z = 3,  = 0 – 3i = –3i,  = –0 – 3i = – 3i  если Re z = 0, то z = iy — чисто мнимое число.

Комплексные равенства:

Равенство двух комплексных чиселозначает равенство дейсствительных частей и равенство мнимых частей этих чисел;равенство комплексного числа нулюозначает, что действительная и мнимая части этого числа равны нулю.

1) 2)

Одно комплексное равенство равносильно системе двух действительных равенств. Эти действительные равенства получаются из комплексного равенства процедурой, которая называется разделением действительных и мнимых частей в комплексном равенстве.

Например,

1) ;

2) .

Геометрическое изображение комплексных чисел Рис. 79

комплексное число zизображается на комплексной плоскости точкойили радиус-вектором этой точки.

Знакz во второй четверти означает, что система декартовых координатбудет использоваться как комплексная плоскость. При этом ось абсциссOX называетсядействительной осью, ось ординат OYназываетсямнимой осью.

2. Модуль, аргумент и тригонометрическая форма комплексного числа (Что такое модуль и аргумент комплексного числа?)

Модулем комплексного числа называется неотрицательное действительное числоr, вычисляемое по формуле

. (1)

Геометрически модуль комплексного числа — это длина радиус-вектора, изображающего число z, или полярный радиус точки (x;y), рис. 79.

Аргумент комплексного числаz — это угол между положительным направлением действительной оси и векторомz(геометрически – это полярный угол точки (x;y)).

Обозначение , причемили(рис. 79).

Формула для вычисления аргумента комплексного числа имеет вид

Аргумент комплексного числа, (2)

причем, при определении углапо его тангенсу обязательно нужно учитывать, в какой четверти на комплексной плоскости расположено числоz:

Замечание (к определению аргумента комплексного числа)

Так как геометрически очевидно (рис. 79), что и, то

Тригонометрическая форма комплексного числа. (3)

Запись z = x + iy называется алгебраической формой комплексного числа z; записьz = r(cos + i sin) называется тригонометрической формой комплексного числаz, при этом .

Примеры (геометрическое изображение и тригонометрическая форма комплексных чисел)

Изобразим на комплексной плоскости следующие числа и запишем их в тригонометрической форме:

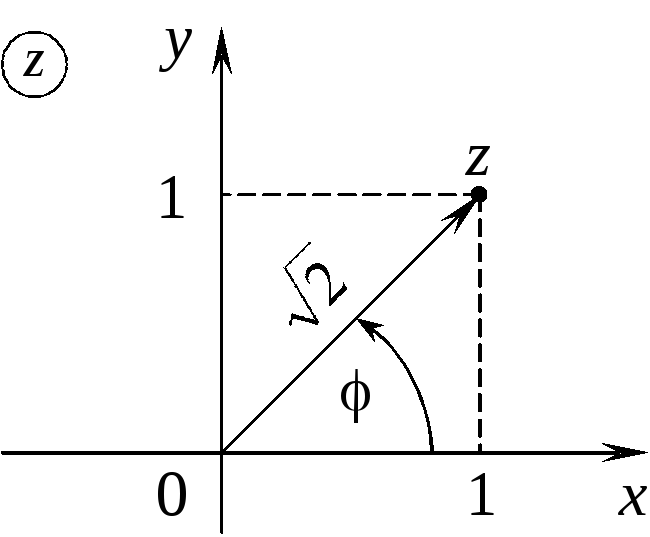
1) z = 1 + i  ,  ;
2)  ,  ;
3)  ,  ;
4) ,;
5) ,; 6) , то есть дляz = 0 будет , не определен.