Нули функции и промежутки знакопостоянства
Нулем
функции
называется такое значение
ее аргумента, при котором значение
функции равно нулю:
.
Множество нулей функции
–
это следующее множество:
.
Промежутком
знакопостоянства функции
называется промежуток значений ее
аргумента, входящий в ООФ,
во всех точках которого функция принимает
значения одного знака: 
или
.
Множества промежутков знакопостоянства
функции
обозначаются следующим образом:
,
.
Пример 2 (нули и промежутки знакопостоянства функции)
Найти множества нулей и промежутков знакопостоянства заданных функций:
1)
2)
Решение
1)
ООФ:
;
данная функция имеет два нуля, которые разбивают ее ООФ на промежутки знакопостоянства функции:
знак функции на каждом из обозначенных
промежутков можно определить по
точке-представительнице промежутка,
если вычислить знак значения функции
в этой точке:
при
;
при
;
при
;
при
;
Т
аким
образом, получено, что
при
или
;
при
;
при
;
Нули функции и промежутки ее знакопостоянства
вместе с ООФдают первичную информацию
о расположении графика функции на
координатной плоскости
:
|
точки
прямая
график будет расположен
выше оси
ниже оси
|
|
и
принадлежат графику;
графиком не пересекается;
при
и
,
при
и
.
2)
ООФ:
;
,
следовательно, функция имеет два нуля;
промежутки знакопостоянства функции:
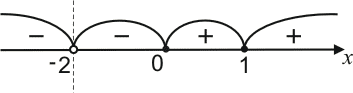
при
илиx= 1;
при
;
при
.
Ответ:
1)
2)
Четность, нечетность функций
Функция
называетсячетной
функцией, если выполняются
следующие два условия:
График четной функции всегда имеет осевую симметрию относительно оси функции (рис.45).
Функция
называетсянечетной функцией,
если выполняются следующие два условия:
График нечетной функции всегда имеет центральную симметрию относительно начала координат (рис.46).
Рис.45 Рис.46
Пример 3 (исследование функций на четность)
Исследовать следующие функции на четность:
1)
;
2)
;
3)
;
4)
.
Решение
1)
;
ООФсимметрична относительно точкиx = 0;
вычисляем
,
используя четность основных элементарных
функций
и
:
;
равенство
выполняется для
,
поэтому данная функция является четной,
ее график будет симметричным относительно
осиOY;
2)
ООФявляется симметричной относительно точкиx = 0;
вычисляем
,
учитывая, что
,
:
равенство
выполняется при
,
поэтому данная функция является нечетной
и ее график будет иметь центральную
симметрию относительно начала координат;
3)
– есть симметрияООФотносительно
точкиx = 0;
вычисляем
:
здесь не выполняется ни одно из равенств
или
,
поэтому данная функция не является ни
четной, ни нечетной, следовательно,
симметрию её графика предсказать нельзя;
4)
ООФне является симметричной относительно точкиx = 0, поэтому свойством четности или нечетности эта функция обладать не может. Следовательно, она относится к функциям общего вида, которые не являются ни четными, ни нечетными.
Ответ:1) функция
является четной;
2) функция
является нечетной;
3) функция
не является ни четной, ни нечетной;
4) функция
не
является ни четной, ни нечетной.
Периодичность функции
Функция
называетсяпериодической
функцией, если существует
число
,
такое что верно равенство
График периодической функции имеет повторяющиеся участки на каждом промежутке длинойT. Наименьшее из чиселTназываетсянаименьшим периодом функции. По умолчанию буквойТобозначают именно наименьший период (рис.47).
Рис.47
Исследование периодической функции и построение ее графика следует проводить на промежутке, длина которого равна наименьшему периоду функции; этот промежуток часто называютосновным промежутком для периодической функции.
Ниже перечислены некоторые свойства периодических функций:
Периодическая функция не может быть задана на множестве, ограниченном сверху или ограниченном снизу.
Например, функция
,
не является периодической.
Если число
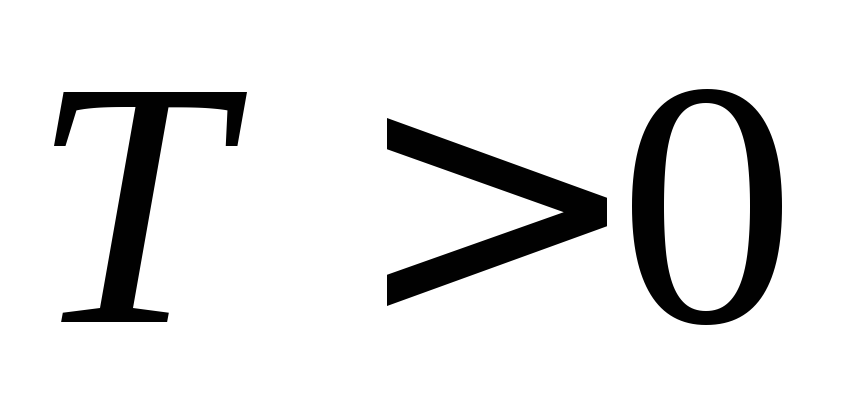является периодом функции
,
то число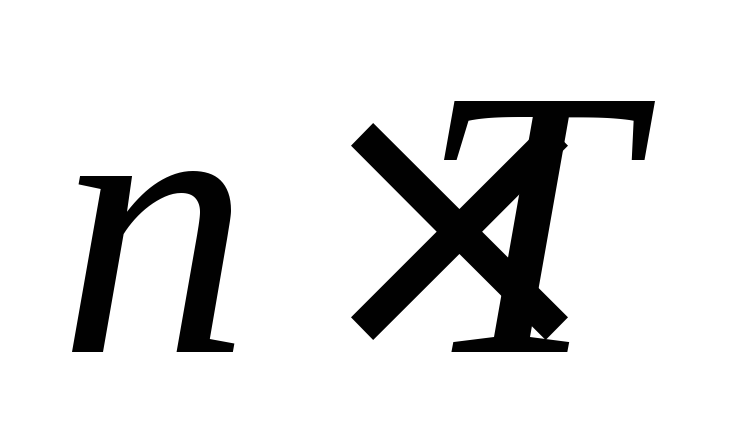
,
где
,
также является ее периодом.
Например, функция
,
является периодической, её наименьший
период
и
числа
,
также являются ее периодами.
Если число
– это наименьший период функции
,
то функция
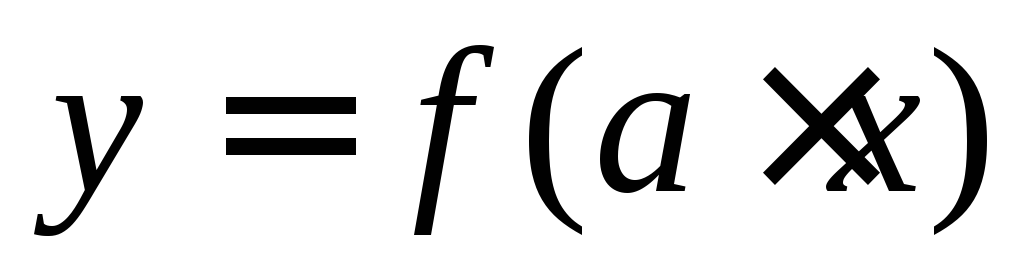является также периодической и ее
наименьший период равен числу
.
Например, функция
,
является периодической и ее наименьший
период равен
.
При сложении двух периодических функций с одинаковыми ООФ получается периодическая функция, причем ее наименьший период делится нацело на
и на
,
где
,
– это наименьшие периоды слагаемых.
Например,
–
периодическая с
,
– периодическая с
– периодическая с
,
так как
и
.
Примеры 4 (определение периодичности функций)
1.
Является ли функция периодической?
Чему равен ее наименьший период?
Решение
Известно, что основная элементарная
функция
является периодической с наименьшим
периодом
.
Проверим равенство
для данной функции:
По выполнению равенства заключаем, что
данная функция является периодической
с периодом
.
Чтобы найти наименьший период, понизим
степень выражения
по известной тригонометрической формуле:
.
Тогда
.
Теперь имеем сумму двух периодических функций:
,
,
,
периодом является любое положительное
число;
следовательно, данная функция
имеет наименьший период
;
поэтому исследовать ее свойства и
строить график достаточно на основном
промежутке, например при
,
а затем сделать периодическое продолжение
на всюООФ.
Ответ:функция
является периодической с наименьшим
периодом
.
2.
Является ли функция периодической?
Решение
Данная сложная функция не является
периодической, так как не является
периодической её промежуточная функция
,
"искажающая" те значения аргументаx, для которых одинаковые
значения имела бы функция
.
Для иллюстрации сказанного проверим расположение нулей данной функции:
Имеем
множество всех нулей функции:
Видим, что нули функции располагаются непериодически на оси OX. Следовательно, данная функция не является периодической (так как в противном случае все её свойства, в том числе и нули, повторялись бы периодически).
Ответ:
функция
не является периодической.
3.Укажите, какие из следующих функций являются периодическими?
1)
;
2)
;
3)
; 4)
.
Решение
Функция периодической не является, так как равенство
не выполняется, например, для точки
,
потому что точка
из-за ограниченности снизуООФ(рис.48);
2) функция периодической не является,
так как равенство
не выполняется, например, для точки
(рис.49);
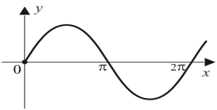
Рис.48 Рис.49
3) функция является периодической с
наименьшим периодом
,
что хорошо видно по ее графику на рис.
50;
4) функция является периодической с
наименьшим периодом
,
что хорошо видно по ее графику на рис.
51;
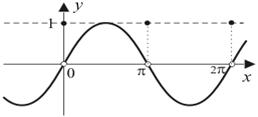
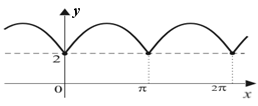
Рис. 50 Рис.51
Ответ:периодическими являются только функции 3) и 4).