Модуль 1 Множества и функции_конспект лекций / Para 09

114

9. Обратная функция: определение, условия существования, график

Содержание

§ 9. Обратная функция: определение, условия существования, график 102

Содержание 102

9.1. Определение обратной функции 102

9.2. Примеры нахождения обратной функции 103

9.3. Взаимно обратные функции в традиционных обозначениях аргумента и функции 105

9.4. Примеры построения графика суперпозиции взаимно обратных функций 106

9.5. Решение задачи о нахождении обратной функции 108

9.6. Упражнения для самостоятельной работы 110

Вопросы для самопроверки 114

Глоссарий 114

1. Определение обратной функции

Рассмотрим числовую функцию y = f(x): , причем отображение множества X на множество Y , описываемое этой функцией, является биективным (рис. 57).

Рис. 57

Так как отображение является взаимно однозначным (биективным), то каждое значение является образом единственного значения ; поэтому может быть рассмотрено обратное отображение или обратная функция, которая обозначается и ставит в соответствие каждому значению единственное значение . При этом обратная функция описывает также биективное отображение. Обе функции и называются взаимно обратными функциями.

Таким образом, необходимым и достаточным условием для существования обратной функции является биективность отображения, описываемого данной функцией .

2. Примеры нахождения обратной функции

Для каждой из данных функций y = f(x) построим обратную функцию :

1)

эта функция задает биективное отображение множеств: , поэтому имеет обратную функцию , ;

2)

эта функция описывает биективное отображение множеств , поэтому имеет обратную функцию ;

3

y

)

эта функция описывает отображение множеств  , которое не является биективным, поэтому обратной функции не имеет;

4)

y

0 -1 1

здесь есть биективность отображения , поэтому данная функция имеет обратную функцию ;

5)

данная функция не имеет обратной функции, так как задает отображение, которое не является взаимно однозначным (биективным). Но если рассмотреть два сужения этой функции (две ветви параболы), то на каждом из них обратная функция есть:

y

; .

Из рассмотренных примеров хорошо видно, что взаимно обратные функции и имеют один и тот же график, а их ООФ и ОЗФ меняются местами. Нахождение аналитического выражения обратной функции сводится к разрешению уравнения относительно x. Если же такое разрешение невозможно, то получится неявное задание обратной функции в виде уравнения .

3. Взаимно обратные функции в традиционных обозначениях аргумента и функции

Часто бывает так, что функция, являющаяся обратной к другой функции, имеет самостоятельное значение и поэтому её аргумент традиционно обозначается через x, а функция через y. Например, известно, что функции и являются взаимно обратными; то же относительно функций и . В этом случае прямая и обратная функция записываются в следующем виде:

и .

Г

y

y

рафики взаимно обратных функций и не совпадают друг с другом, но имеют осевую симметрию относительно прямой y = x - биссектрисы первого и третьего координатных углов. На рисунке 58 приведены пары взаимно обратных функций и их графики.

y = x

Рис. 58

Очевидно, что взаимно обратные функции «гасят» друг друга, но только на множестве тех значений аргумента, для которых соблюдается биективность отображений .

Например, 1) только при , только при ;

2) только при , только при ;

3) при , только при ;

4) при , только при .

4. Примеры построения графика суперпозиции взаимно обратных функций

Построим графики нескольких функций, записанных как суперпозиция известных взаимно обратных функций.

1. и

Решение

ООФ:	-1 y=sin(arcsinx)

ООФ: ;

функция является периодической с , основной промежуток ;

для будет ;

чтобы построить график для остальных значений , составим следующую таблицу значений:

x
sinx				0				0
y=arcsin(sinx)				0				0

На основании закономерности, наблюдаемой при построении таблицы, запишем аналитическое выражение в формее ее кусочного задания. Графики обеих суперпозиций приведены на рис. 54.

Ответ:

2. и

Решение

1) ООФ: (рис. 55)

Рис. 55

2) ООФ: (рис.56)

Рис. 56

Ответ:

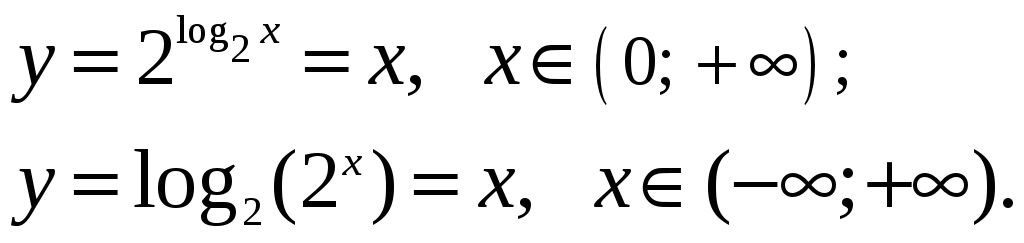
5. Решение задачи о нахождении обратной функции

Постановка задачи

Для каждой из следующих функций найти обратную функцию . Построить графики обеих функций в одной системе координат, записать для каждой функции область определения и область значений:

1. ; 2. .

Решение

1. Строим график функции и проверяем биективность отображения множеств, описываемого этой функцией:

y

-1	графиком является часть квадратичной параболы типа , имеющей вершину в точке (-1;2); по графику определяем, что имеем биективное отображение , следовательно обратная функция существует.

Для нахождения обратной функции сначала разрешаем уравнение относительно x:

, где ;

получилась обратная функция в виде

.

Теперь в обратной функции переобозначаем аргумент на x, а

функцию на y:

, где ;

это получилась обратная функция в виде

.

y=f -1(x) y

Строим графики обеих взаимно обратных функций и в одной системе координат и подтверждаем их симметричность относительно прямой y = x:

Ответ: если , то ;

, ; , .

2. ;

так как отображение, задаваемое данной функцией, является биективным, то обратная функция существует.

Выражаем x через y из равенства, задающего данную функцию:

;

переобозначим y на x, а x на y: ;

это и есть искомая обратная функция.

Строим графики обеих взаимно обратных функций в одной системе координат, подтверждаем их симметричность относительно прямой и записываем ответ.

Ответ: если , то ;

,;

.

6. Упражнения для самостоятельной работы

1. Для каждой из следующих функций найдите обратную функцию. Постройте графики обеих функции в одной системе координат и запишите их ООФ и ОЗФ.

1) ; 3) ;

2) ; 4) .

2. Постройте графики следующих функций, записанных как суперпозиция известных взаимно обратных функций:

1) и ;

2) и .

Ответы к упражнениям для самостоятельной работы

1.	1) если , то ; ; ;
	2) если , то ; , ; , ;	y y=f -1(x) y
	3) если , то ; , ; ,;

	4) если , то ; , ; , .
2.	1) ;		y ,
	2) ;			x 0

Вопросы для самопроверки

1. Что такое обратная функция?

2. Что называется взаимно обратными функциями?
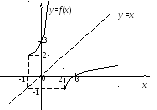