128

10. Классификация функций. Алгебраические и трансцендентные функции. Рациональные дроби Содержание

§ 10. Классификация функций. Алгебраические и трансцендентные функции. Рациональные дроби 115

10.1 Классификация функций: основные элементарные, элементарные и неэлементарные функции 115

10.2 Алгебраические и трансцендентные функции 117

10.3 Рациональные дроби 119

10.4 Обратно пропорциональная зависимость и дробно линейная функция 123

10.5 Упражнения для самостоятельной работы 125

Пример (построение графика дробно-линейной функции) 125

Построить график функции 125

Решение 125

Сначала выделим целую часть в неправильной рациональной дроби: 125

; ООФ: ; 125

Теперь можно построить график данной функции, если использовать известные преобразования графиков и последовательно строить графики 125

125

Вопросы для самопроверки 128

Глоссарий 128

10.1 Классификация функций: основные элементарные, элементарные и неэлементарные функции

Аналитически заданные функции, записанные в явной форме, принято разделять на основные элементарные функции, элементарные функции и неэлементарные функции.

Основными элементарными функцияминазываются следующие функции:

• постоянная функция ;

• степенная функция ;

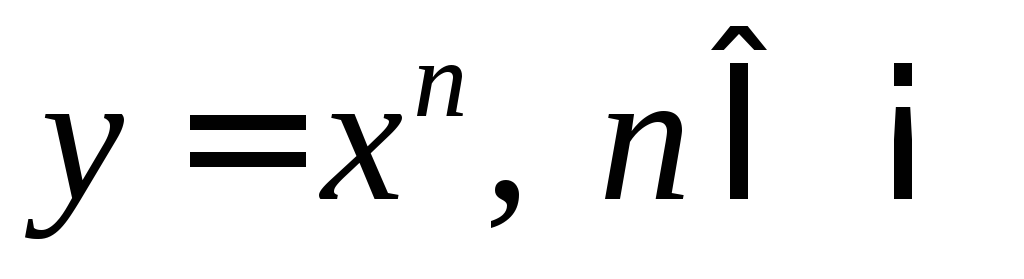• показательная функция 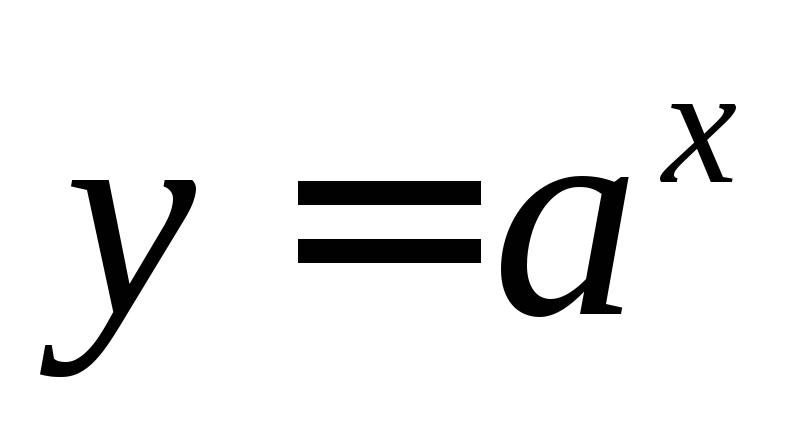, гдеa > 0,a  1;

• логарифмическая функция 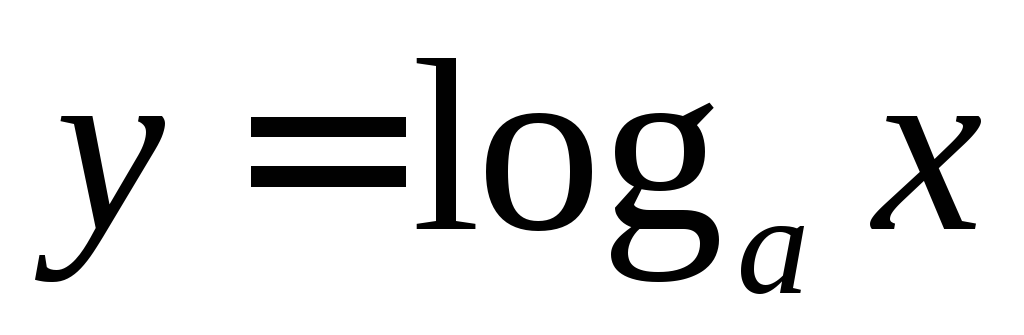, гдеa > 0,a  1;

• тригонометрические функции ;

• обратные тригонометрические функции , ;

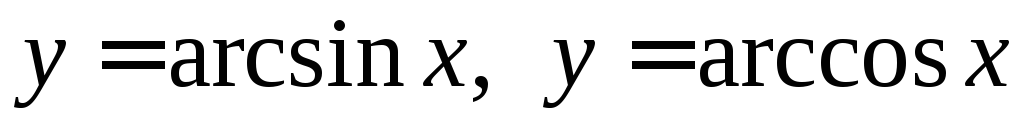• гиперболические функции .

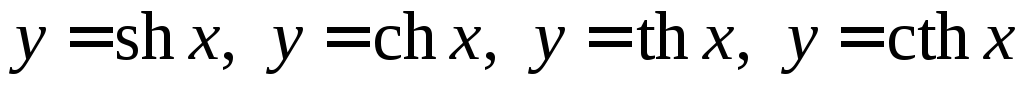Большинство этих функций изучались в элементарной математике. Их определения, основные свойства и графики нужно знать на память. Повторению этих функций, а также определению гиперболических функций посвящен §10 изучаемой темы.

Элементарной функциейназывается функция, которая записывается одной формулой вида, где справа стоящее выражениесоставлено из основных элементарных функций и чисел при помощи конечного числа операций сложения, вычитания, умножения, деления и суперпозиции функций.

Пример (элементарные функции)

;;; .

Неэлементарной функциейназывается функция, которая не относится к элементарным; например, если она не записывается одной формулой или содержит бесконечное число арифметических операций.

Примеры (неэлементарные функции)

1)

2) функция Дирихле:

3) .

Далее в курсе математического анализа появятся еще так называемые специальные функции, которые не попадают в рассмотренную классификацию.

10.2 Алгебраические и трансцендентные функции

В множестве элементарных функций выделяют алгебраические и трансцендентные функции.

Алгебраическими функцияминазывают целые многочлены, рациональные дроби и иррациональные функции.

Например, ; ; .

Трансцендентными функцияминазывают элементарные функции, не являющиеся алгебраическими.

Например,;;

Среди алгебраических функций выделяются целые многочлены и рациональные дроби.

Целым многочленом (полиномом) степени n относительно переменной x называется функция следующего вида:

(1)

здесь — степень многочлена;

– коэффициенты многочлена (числа или параметры);

­– старший коэффициент.

Например,

1) – многочлен первой степени;

2) — квадратный трехчлен, или квадратичная функция;

3) — многочлен нулевой степени;

4) - многочлен 10-й степени.

График квадратичной функции

Функцияназываетсяквадратичной функцией.

Число называетсядискриминантом квадратного трехчлена.

Графиком квадратичной функции является парабола, ее положение относительно координатных осей определяется знаком старшего коэффициента aи значением дискриминантаD (см. таблицу на рис. 59).

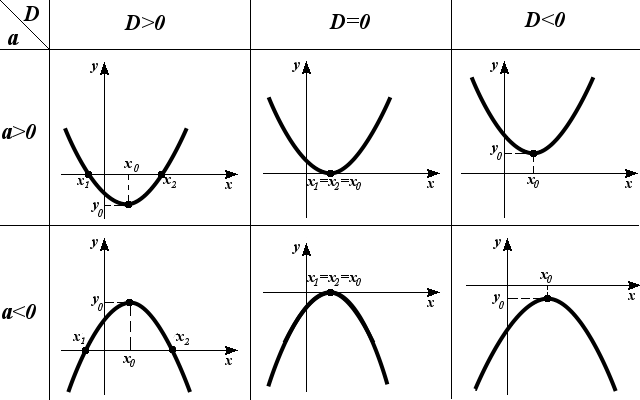
Рис.59

Здесьx₁,x₂— это нули квадратичной функции, вычисленные как корни квадратного уравнения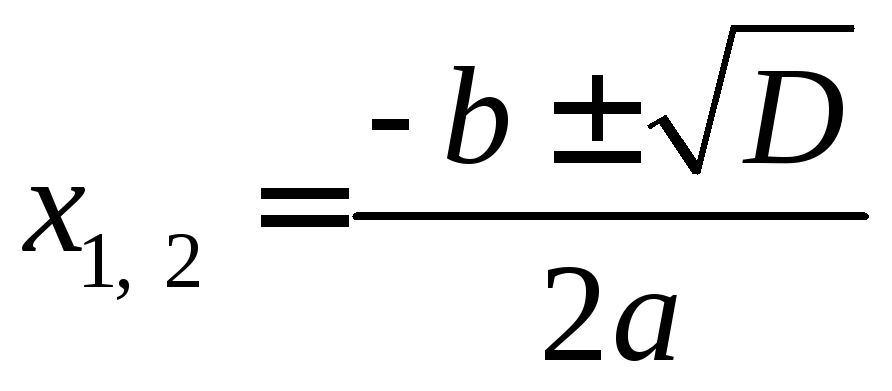, если ;— абсцисса вершины параболы (точка экстремума);— ордината вершины (экстремум квадратичной функции).

Иррациональные функции— это такие функции, не являющиеся рациональными, которые могут быть заданы композицией конечного числа рациональных функций, степенных функций с рациональными показателями и четырех арифметических действий.

Например,

1) ; 3);

2) ; 4).