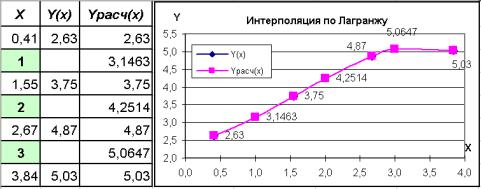
значений функции Yрасч(Х). По данным этой таблицы построим точечную диаграмму двух функций Y(X) и Yрасч(Х). Таблица и диаграмма приведены на рис. 12.
Рис. 12. Таблица и диаграмма, отображающая результаты интерполяции по Лагранжу
1.5. Интерполяционные многочлены Ньютона
Для интерполяции функций, заданных таблицами с равноотстоящими значениями аргумента
X i +1 −X i =h |
( i =0 ,1,2 ,... ,n −1) |
(18) |
построение интерполяционных формул и вычисление по этим формулам заметно упрощается. В записях этих интерполяционных алгоритмов используются разности между значениями функции в соседних узлах интерполяции.
1.5.1. Конечные разности |
|
Конечной разностью первого порядка называется |
|
yi = ( Yi +1 − Yi ) ( i = 0 ,1,2 , ... ,n − 1 ). |
(19) |
Из конечных разностей первого порядка образуются конечные разности второго порядка [ 4 ]:
2 yi = yi+1 − yi = ( yi+2 |
− yi +1 ) −( yi +1 |
− yi |
) = |
(20) |
= ( yi+2 − 2 yi +1 + yi ) |
|
|
(i = 0,1,2, ... , n − 2) |
|
|
|
|
Аналогично определяются конечные разности третьего, четвёртого и более высоких порядков.
Для вычисления конечных разностей обычно создаются таблицы, вид которых приводится ниже.
|
|
|
|
Таблица 1. Алгоритм построения конечных разностей |
||
|
|
|
|
|
|
|
i |
Х |
Y |
y |
2y |
3y |
4y |
0 |
X0 |
Y0 |
y0= Y1- Y0 |
2y0= y1- y0 |
3y0= 2y1- 2y0 |
4y0= 3y1- 3y0 |
1 |
X1 |
Y1 |
y1= Y1- Y2 |
2y1= y2- y1 |
3y1= 2y2- 2y1 |
|
2 |
X2 |
Y2 |
y2= Y3- Y2 |
2y2= y3- y2 |
|
|
3 |
X3 |
Y3 |
y3= Y4- Y3 |
|
|
|
4 |
X4 |
Y4 |
|
|
|
|
9
В таблице 2 приведём числовой пример формирования таблицы конечных разностей для таблично заданной функции.
Таблица 2. Пример построения таблицы конечных разностей для функции Y(x)
i |
Х |
Y(X) |
y |
2y |
3y |
4y |
0 |
0,0 |
0,696 |
1,579 |
-2,685 |
8,246 |
-25,061 |
1 |
0,4 |
2,275 |
-1,106 |
5,561 |
-16,815 |
|
2 |
0,8 |
1,169 |
4,455 |
-11,254 |
|
|
3 |
1,2 |
5,624 |
-6,799 |
|
|
|
4 |
1,6 |
-1,175 |
|
|
|
|
1.5.2. Интерполяционные формулы Ньютона
Для функций, заданных таблицами с постоянным шагом изменения аргумента, наиболее часто используются первая или вторая формулы Ньютона, в которых интерполяционная функция определяется как многочлен вида:
P(I)(x)=a |
0 |
+a (x−X )+a |
2 |
(x−X )(x−X )+...+a (x−X )(x−X ) ...(x−X |
) |
(21) |
|||||
n |
1 |
0 |
0 |
1 |
n |
0 |
1 |
n−1 |
|||
при интерполяции от нулевого узла Х0 или
P (II) (x)=b +b (x−X )+b (x−X) (x−X )+...+b (x−X)(x−X ) ...(x−X ) |
(22) |
|||||||
n |
0 1 |
n 2 |
n |
n−1 |
n n |
n−1 |
0 |
|
при интерполяции от узла Хn.
Значения коэффициентов ai и bi в формулах (21) или (22) находятся из условий Лагранжа, определяющих в узлах интерполяции совпадение значений
интерполирующей функции со значением табличнозаданной функции |
|
Pn ( xi ) = Yi |
(23) |
(см. также формулу (2) в общей постановке задачи интерполяции). Полагая Х=Х0 , в формуле (21) получим
Pn(Х0)=a0=Y0 .
Аналогично для Х=Х1
Pn(Х1)=a0+a1(X1-X0)=Y1 ,
и далее
a1=(Y1-Y0)/(X1-X0)
или, используя введённые обозначения,
a1= y0/(1!h).
Продолжая подстановки значений Хi , получим
Pn(Х2)=a0+a1(X2-X0)+ a2 (X2-X0)(X2-X1) =Y2 ,
и далее |
|
|
|
a2*2h2=Y2 - a0 - a1*2h = Y2 - Y0 - |
y0/h*2h = Y2 - 2 Y1 + Y0 = 2y0 |
||
откуда |
|
|
2 y0 . |
a |
|
= |
|
|
2 |
|
2!h2 |
Проведя аналогичные преобразования для Х=Х3 и Х=Х4, получим
10
|
|
|
a |
|
= |
3 y0 , |
a |
|
= |
4 y0 |
, |
..., a |
|
= |
|
k y0 |
|
(24) |
|
|
|
|
|
4 |
4!h4 |
k |
|
k!hk |
|||||||||||
|
|
|
|
3 |
|
3!h3 |
|
|
|
|
|
|
|
|
|||||
|
Подставив (24) в (21), получим |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Pn |
( x) = y0 + |
y0 |
( x − x0 ) + |
|
2 y20 ( x − x0 )( x − x1 ) + ... + |
|
n yn0 |
( x − x0 )( x − x1 )...( x − xn−1 ) |
(25) |
||||||||||
|
|
h |
|
|
2!h |
|
|
|
|
|
|
n!h |
|
|
|
|
|||
На примере исходных данных, приведенной в таблице 2, рассмотрим методику вычислений значений интерполируемой функции для значений аргумента х, не совпадающих с узловыми точками таблицы. Вычислим значение функции Y для Х=1.
P4(1)=0,696+1,579/0,4*(1-0,0)+(-2,685)*(1-0,0)*(1-0,4)/(2*0,42) + 8,246*(1-0,0)*(1-0,4)*(1-0,8)/(6*0,43)+ (-25,06)*(1-0,0)*(1-0,4)*(1-0,8)*(1-1,2)/(24*0,44) = 3,1649
1.5.3. Организация ручных вычислений по первой формуле Ньютона
Рассмотрим пример выполнения ручных вычислений по первой формуле Ньютона.
Задана таблица значений функции, содержащая 4 узла:
|
|
|
Х |
|
1 |
|
2 |
|
3 |
|
4 |
|
|
||||
|
|
|
Y |
|
2 |
|
4 |
|
7 |
|
6 |
|
|
||||
Для данных этой таблицы вычислим таблицу конечных разностей |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
i |
|
Xi |
|
|
Yi |
|
Yi |
|
2Yi |
|
3Yi |
|||||
|
0 |
|
1 |
|
|
2 |
|
2 |
|
1 |
|
-5 |
|||||
|
1 |
|
2 |
|
|
4 |
|
3 |
|
-4 |
|
|
|
||||
|
2 |
|
3 |
|
|
7 |
|
-1 |
|
|
|
|
|
|
|||
|
3 |
|
4 |
|
|
6 |
|
|
|
|
|
|
|
|
|
||
Вычислим значения коэффициентов полинома Ньютона |
|
|
|||||||||||||||
|
|
|
a0=Y0=2; |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
a1= |
y0/h= 2/1!/1=2; |
|
|
|
|
|
|
|
|
|||||
|
|
|
a2= 2Y0/(2!h2)=1/(2!*12) =0,5; |
|
|
|
|
|
|||||||||
|
|
|
a3= |
3Y0/(3!h3)=-5/6. |
|
|
|
|
|
|
|
|
|||||
Используя вычисленные значения коэффициентов a0 ,a1 , a2 , a3 запишем формулу для полинома Ньютона:
P3(x)=2+2(x-1)+0,5(x-1)(x-2)-5/6(x-1)(x-2)(x-3)= =-5/6x3+5,5x2-26/3x+6
Эту формулу мы можем использовать для вычисления значений функции Y(x) в любой точке интервала от х=1 до х=4.
1.5.4. Реализация алгоритма интерполяции по первой формуле Ньютона в среде программы Microsoft Excel
1.Введем в таблицу на листе Excel исходные данные, записанные в столбцах Х и Y(X) таблицы 2.
2.По формулам (19), (20) и формулам, приведённым в таблице 1, сформируем таблицу 2 - таблицу конечных разностей до четвёртого
11
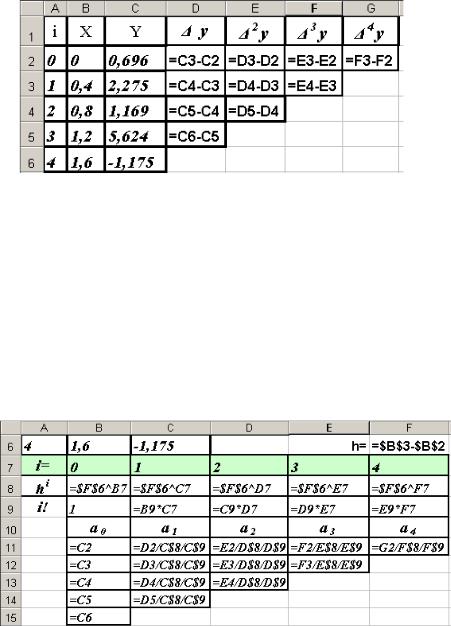
уровня. Эти формулы, введенные в ячейки таблицы Excel, приведены на рис. 13.
Рис. 13. Формулы, использованные для вычисления значений конечных разностей функции Y(Х) в таблице 2
3.В ячейку G6 для вычисления значения шагового приращения аргумента h введем формулу "=$В$3-$В$2".
4.В ячейки строки 7 введём значения индекса i, определяющего индекс строки таблицы.
5.В ячейках строки 8 вычислим степени hi, а в ячейках строки девять запишем формулы для определения факториалов i!.
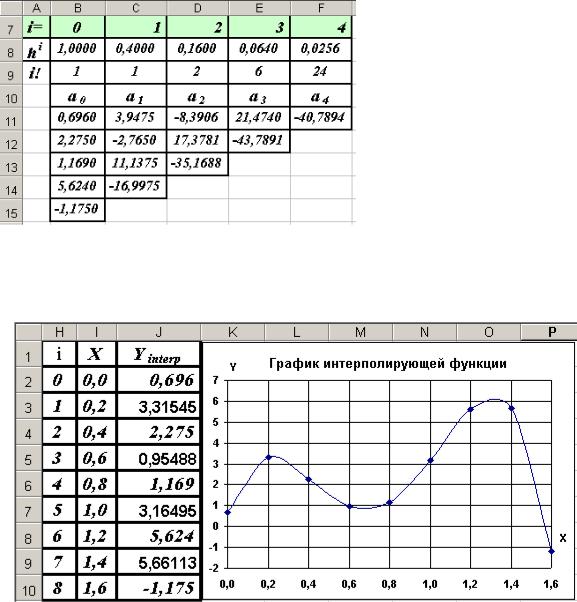
6.На рис. 14 показаны формулы, используемые в таблице для вычисления
значений коэффициентов ai (i=0,1,2,3,4) для вычислительной формулы полинома Ньютона.
Рис. 14. Формулы, введенные в ячейки листа Excel, для вычисления коэффициентов интерполирующего многочлена Ньютона
Для формирования этой таблицы достаточно ввести в ячейку В11 формулу "=С2" и протянуть её до ячейки В15 (формируется столбец ссылок на ячейки со значениями Yi)
7.На рис. 15 приведена таблица рис.14. в режиме отображения числовых значений, вычисленных по формулам рис. 14.
8.Для выполнения вычислений значений интерполирующего полинома Ньютона в столбцах H, I и J сформируем разреженную таблицу. В столбец Н запишем номера строк таблицы от 0 до 8. В столбец I записываем значения аргумента Х от Х0 = 0 до Хk = 1,6.
9.В ячейку J2 и введём формулу для вычисления значения интерполирующего полинома Ньютона:
12
=$B$11+(I2-$B$2)*$C$11+ (I2-$B$2)*(I2-$B$3)*$D$11+ (I2-$B$2)*(I2-$B$3)*(I2-$B$4)*$E$11+
(I2-$B$2)*(I2-$B$3)*(I2-$B$4)*(I2-$B$5)*$F$11
Здесь $B$11, $C$11, $D$11, $E$11, $F$11 - ссылки на коэффициенты ai
(i=0,1,2,3,4); I2 - ссылка на ячейку со значением аргумента x для точки, в которой вычисляется значение интерполирующего полинома Ньютона, $B$2, $B$3, $B$4, $B$5 - ссылки на ячейки, в которых записаны значения аргументов Xi (i=0,1,2,3,4).
Рис. 15. Результаты вычислений коэффициентов ai (i=0,1,2,3,4) по формулам рис. 14
10.Протянув формулу, записанную в ячейку J2, по столбцу до ячейки J10, получим значения интерполирующего полинома для всех точек вектора Х. Результаты вычислений и график, построенный по таблице значений, показан на рис. 16.
Рис. 16. Таблица и график с результатами интерполяции
11.График, построенный по результатам интерполяции, сглажен. Для этого после выделения графика в окне "Формат ряда данных" на вкладке
"Вид" включаем флажок "Сглаженная линия".
13