Лекция 2

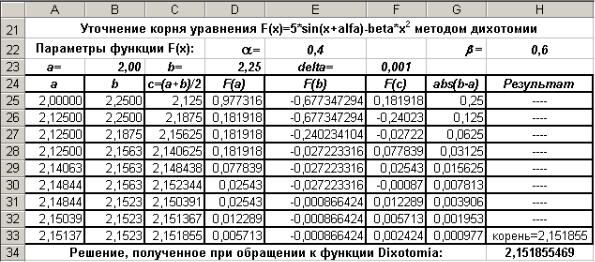
В строке 34 этой таблицы приведены результаты решения, полученные после применения функции, в которой метод дихотомии реализован на языке Visual Basic. Текст этой функции приведён ниже.

Рис. 3.10. Результаты уточнения корня методом дихотомии

Текст функции VBA, реализующей алгоритм метода дихотомии.

Function Dixotomia(a As Double, b As Double, delta As Double, alfa As Double, beta As Double)

Dim i As Integer ' i - счётчик числа итераций

Dim c As Double

If Fsin(alfa, beta, a) * Fsin(alfa, beta, b) > 0 Then MsgBox ("Интервал [a, b] выбран неправильно") Exit Function

End If i = 0 Do

c = (a + b) / 2

If Fsin(alfa, beta, a) * Fsin(alfa, beta, c) < 0 Then b = c Else a = c i = i + 1

Loop Until Abs(b - a) < delta Dixotomia = (a + b) / 2

End Function

3.2.4. Метод хорд

Метод хорд [5] так же, как и метод дихотомии, предназначен для уточнения корня на интервале, определённом при проведении процедуры отделения корней. На концах этого интервала [a, b] исследуемая функция имеет значения F(a) и F(b) с разными знаками. Очередное приближение, определяемое в методе хорд, находится в

Лекция 2

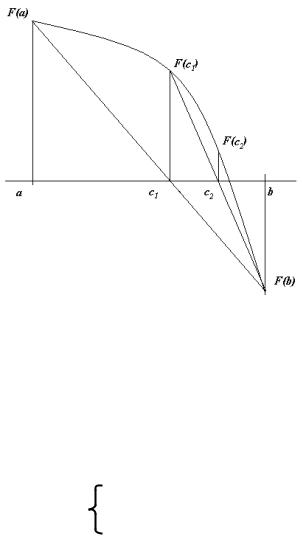
точке пересечения оси абсцисс прямой, соединяющей точки F(a) и

F(b).

Рис. 3.11. Диаграмма алгоритма метода хорд

Координата этой точки определяется из уравнения прямой, соединяющей точки F(a) и F(b). Определив уравнение прямой как функцию

Y(X) = kX+D,

координата точки пересечения прямой с осью абсцисс определяется из решения системы уравнений

F(a)=ka+D,

F(b)=kb+D.

Решая эту систему, определим значения параметров k и D

При условии Y(c)= kc+D=0 определяем значение с:

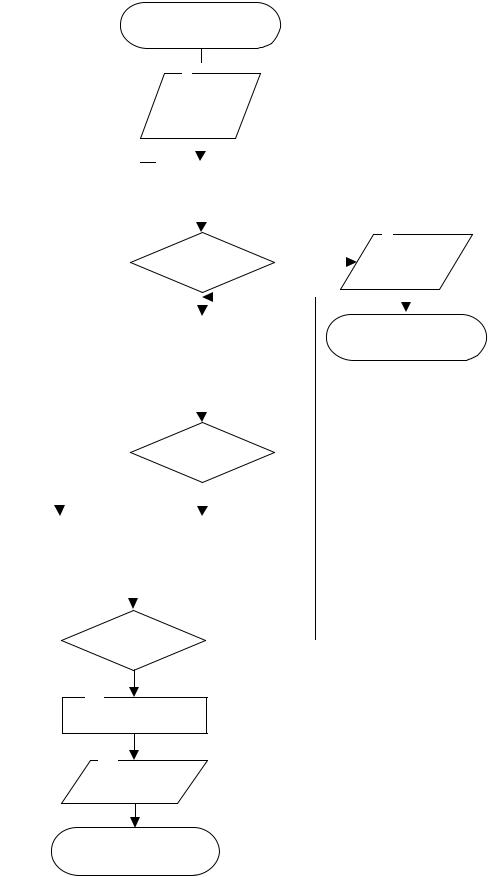
Блок-схема алгоритма метода хорд приведена на рис. 3.12. Результаты применения метода хорд для уточнения значения

корня в выделенном интервале [2,00; 2,25] приведены на рис. 3.13. Решение получено после выполнения трёх итераций.

Лекция 2

Function Horda(a,b,δ)

1

Ввод

параметров a, b,δ

нет

Horda:=c

11

Рис. 3.12. Блок-схема алгоритма метода хорд

Ниже приводится текст функции VBA, реализующей алгоритм метода хорд.

Лекция 2

Public Function Horda(a As Double, b As Double, delta As Double, alfa As Double, beta As Double)

Dim С As Double, Fa As Double, Fb As Double, Fс As Double Fa = Fsin(alfa, beta, a)

Fb = Fsin(alfa, beta, b) If Fa * Fb > 0 Then

MsgBox ("Интервал [a, b] выбран неправильно") Exit Function

End If Do

С = a - (b - a) / (Fb - Fa) * Fa Fс = Fsin(alfa, beta, С)

If Fс * Fa > 0 Then b = С: Fb = Fс Else a = С: Fa = Fс Loop Until Abs(b - a) < delta

Horda = С End Function

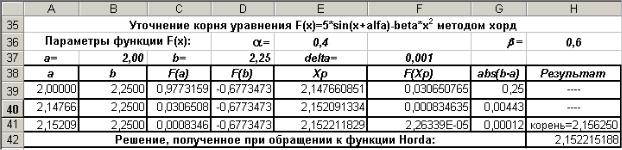
Рис. 3.13. Результаты применения метода хорд для уточнения корня функции

F(x)=5*sin(x+α)-β*x2

3.2.5.Метод простых итераций

Витерационных методах, которые иначе называют методами последовательных приближений, многократно повторяется - "итерируется" (от латинского "итерацио" - повторение) некоторый единообразный вычислительный процесс. В результате каждой итерации получаются всё более точные приближения к искомому решению.

Вобщем виде итерационная формула определяется приведением уравнения (3.1) к равносильной форме

Х=φ(X). (3.9)

После записи уравнения (3.1) в виде (3.9) определяется начальное значение Х0 - "нулевое приближение". Последующие

Лекция 2

приближения вычисляются по формулам Х1=φ(X0), Х2=φ(X1),…, или в общем виде

Возможны два варианта поведения итерационного процесса.

В первом случае итерационный процесс сходится, последовательные приближения Хi стремятся к некоторому конечному пределу, который и является решением уравнения (3.1). Во втором варианте процесс расходится, конечного предела приближений не существует. Из расходимости процесса не следует, что решения уравнения (3.1) не существует, а следует только то, что способ построения итерационного процесса выбран неудачно.

Покажем это на простом примере. Сравним две формы

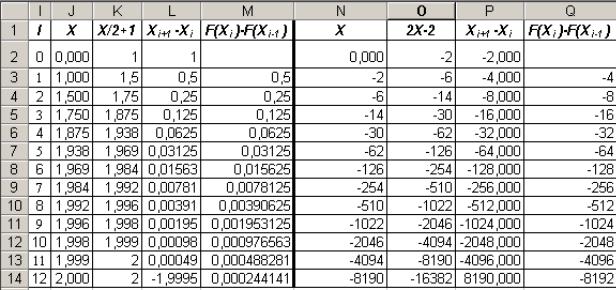
Эти уравнения имеют очевидное решение X=2. Определим начальное значение Х0 =0 и вычислим последовательные значения Хi для итерационных процессов, определяемых формулами (3.11) и (3.12). Результаты итерационных вычислений по формулам (3.11) и (3.12) приведены на рис. 3.14.

Рис. 3.14. Сравнительная таблица итерационных процессов для двух представлений равносильных уравнений (3.11) и (3.12)

Процесс, определяемый уравнением (3.11) сходится, а процесс (3.12) - расходится.