
ИНФОРМАТИКА_1 / PDF_Inform_2курс / PDF_МЕТОДИЧКИ_2-й_семестр / Задания к ЛР Интерполяция
.pdf
Задания к лабораторной работе "Интерполяция таблично заданных функций"
Порядок выполнения вычислений
1.По таблице значений функции (2), используя формулу линейной интерполяции (1), вручную вычислить значение интерполируемой функции в точке (Х2+Х3)/2.
Y(X)=Y(Xi)+ |
Y(Xi+1)−Y(Xi) |
(X−Xi) (i =0,1,2,...,n) |
(1) |
|
|||
|
Xi+1 −Xi |
|
|
2.В таблице Excel сформировать таблицу (2), реализуя формулу
(1)как формулу Excel, вычислить значения интерполирующей функции YЛ(X) в точках определяющих середины отрезков
[xi, xi+1] (i=0, 1,… n) и сформировать расширенную таблицу (3), включающую вычисленные значения интерполируемой функции.
|
|
Х |
|
Х0 |
|
Х1 |
|
|
… |
Хn |
|
(2) |
||||
|
|
Y1(X) |
Y(Х0) |
|
Y(Х1) |
|
|
… |
Y(Хn) |
|
||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
(Хn-1+Хn)/2 |
|
|
|||||
Х |
Х0 |
|
(Х0+Х1)/2 |
Х1 |
|
(Х1+Х2)/2 |
… |
|
Хn |
(3) |
||||||
YЛ(X) |
Y(Х0) |
Y(Х0+Х1)/2 |
Y(Х1) |
Y(Х1+Х2)/2 |
… |
|
Y(Хn-1+Хn)/2 |
Y(Хn) |
||||||||
3.Вычислить коэффициенты канонического интерполирующего полинома и сформировать строку с вычисленными по формуле канонического полинома значениями. Сформированную строку YК(X) подключить к таблице (3).
4.По таблице значений функции (1) составить формулу интерполяционного многочлена Лагранжа. Используя полученную формулу, вручную вычислить значение интерполируемой функции в точке (Х2+Х3)/2.
5.Сформировать строку таблицы YЛ(X) со значениями интерполирующей функции, вычисленными по формуле Лагранжа в таблице Excel.
6.Записать таблицу конечных разностей. Вручную по формуле Ньютона вычислить значение интерполируемой функции в точке (Х2+Х3)/2.
7.Выполнить формирование строки таблицы YН(X) со значениями интерполирующей функции, вычисленными по формуле Ньютона.
1 |
Любимов Е.Б. |
|
8.По строкам сформированной таблицы построить графики четырёх функций.
Инструкция по выполнению лабораторной работы на ЭВМ
После выполнения ручных вычислений можно перейти к реализации решения на листе книги Excel.
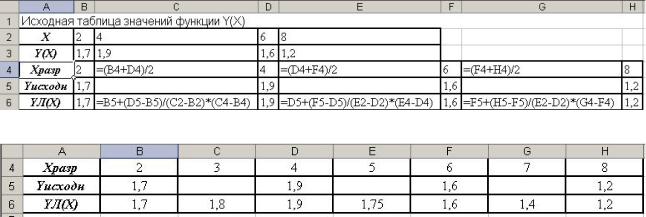
1.После текстового описания постановки задачи на листе книги Excel формируется таблица с исходными данными,
определяющими табулируемую функцию (рис. 1)
Исходная таблица значений функции Y(X)
X |
2 |
4 |
6 |
8 |
Y(X) |
1,7 |
1,9 |
1,6 |
1,2 |
Рис. 1. Таблица данных, определяющих исследуемую функцию
2.Реализуя формулу линейной интерполяции (1) в ячейках таблицы
(3)на листе книги Excel вычисляем значения интерполируемой функции в строке результирующей таблицы (рис.4). На рис.3 эта строка
Рис.3. Реализация формулы линейной интерполяции в ячейках таблицы Excel
Рис.4. Результаты вычислений по формуле линейной интерполяции
3.Выполняем вычисление коэффициентов канонического полинома.
a)формула канонического полинома:
ϕ ( x ) = Pn ( x ) = c 0 + c 1 x + c 2 x 2 + . .. + c n x n
b)по степеням xi формируем матрицу коэффициентов канонического полинома и вектор правых частей системы уравнений (рис.5).
2 |
Любимов Е.Б. |
|
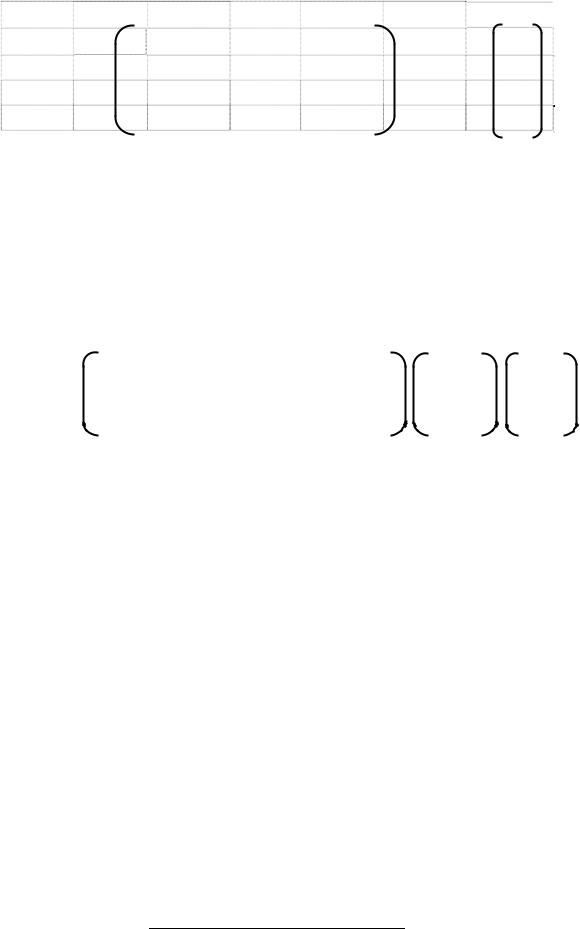
i |
0 |
1 |
|
2 |
3 |
YT |
А= |
|
1 |
2 |
4 |
8 |
1,7 |
|
1 |
4 |
16 |
64 |
1,9 |
|
|
|
1 |
6 |
36 |
216 |
1,6 |
|
|
1 |
8 |
64 |
512 |
1,2 |
Рис.5. Формирование матрицы и вектора правых частей системы линейных алгебраических уравнений, используемой для определения коэффициентов канонического полинома
c)Используя функцию МОБР(), вычисляем значения элементов обратной матрицы и, решив систему линейных алгебраических уравнений, определяем вектор коэффициентов канонического полинома и проверяем правильность полученного решения.
|
|
|
|
|
C |
Yпров |
А-1= |
4,000 |
-6,000 |
4,000 |
-1,000 |
0,6000 |
1,7 |
-2,167 |
4,750 |
-3,500 |
0,917 |
0,8417 |
1,9 |
|
|
0,375 |
-1,000 |
0,875 |
-0,250 |
-0,1625 |
1,6 |
|
-0,021 |
0,063 |
-0,063 |
0,021 |
0,0083 |
1,2 |
d)Используя вычисленные значения коэффициентов, по формуле канонического полинома вычисляем значения интерполируемой функции (рис.6).
X |
2 |
|
3 |
4 |
5 |
6 |
7,0000 |
8 |
YK(X) |
|
1,7 |
1,8875 |
1,9 |
1,7875 |
1,6 |
1,3875 |
1,2 |
Рис.6. Результаты вычислений по формуле канонического полинома
e) Выполняем вычисления по формуле полинома Лагранжа.
L3(x) =l0 (x) +l1(x) +l2 (x) +l3(x)
где: li(x)= qi(x-x0)(x-x1)·(x-x2)(x-x3),
q0=Y0/(x0-x1)/(x0-x2)/(x0-x3) q1=Y1/(x1-x0)/(x1-x2)/(x1-x3) q2=Y2/(x2-x0)/(x2-x1)/(x2-x3) q3=Y3/(x3-x0)/(x3-x1)/(x3-x2)
и
l0(x)= q0(x-x1)·(x-x2)·(x-x3), l1(x)= q1(x-x0)·(x-x2)·(x-x3), l2(x)= q2(x-x0)·(x-x1)·(x-x3), l3(x)= q3(x-x0)·(x-x1)·(x-x2).
3 |
Любимов Е.Б. |
|

Вычисляем |
таблицу |
значений |
коэффициентов |
и |
|||||||
интерполирующего полинома Лагранжа: |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
X |
2 |
|
3 |
4 |
5 |
|
6 |
7 |
8 |
|
|
l0(x) |
1,7 |
|
0,5313 |
0 |
-0,1063 |
|
0 |
0,1063 |
|
0 |
|
l1(x) |
0 |
|
1,7813 |
1,9 |
1,0688 |
|
0 |
-0,5938 |
|
0 |
|
l2(x) |
0 |
|
-0,5 |
0 |
0,9 |
|
1,6 |
1,5 |
|
0 |
|
l3(x) |
0 |
|
0,075 |
0 |
-0,075 |
|
0 |
0,375 |
|
1,2 |
|
YL(X) |
1,700 |
|
1,888 |
1,900 |
1,788 |
|
1,600 |
1,388 |
|
1,200 |
|
f)Для вычисления значений интерполируемой функции с использованием полинома Ньютона предварительно сформируем таблицу конечных разностей.
i |
X |
Y |
yi |
2yi |
3yi |
hi |
i! |
h= |
2,00000 |
0 |
2 |
1,7 |
0,2 |
-0,5 |
0,4 |
1 |
1 |
a0 |
1,70000 |
1 |
4 |
1,9 |
-0,3 |
-0,1 |
|
2 |
1 |
a1 |
0,10000 |
2 |
6 |
1,6 |
-0,4 |
|
|
4 |
2 |
a2 |
-0,06250 |
3 |
8 |
1,2 |
|
|
|
8 |
6 |
a3 |
0,00833 |
Ниже приводится рисунок, на котором этот же фрагмент таблицы Excel в режиме отображения формул.
Рис.7. Формулы записанные в таблицу для вычисления конечных разностей и коэффициентов многочлена Ньютона
Функция ТРАНСП() использована в этом фрагменте для преобразования векторов Х и Y исходной таблицы в формат векторастолбца.
g)Значения, вычисленные по формуле Ньютона были получены для трёх вариантов её реализации:
-с использованием функции пользователя, записанной на
VBA;
-с использованием формул Ньютона, в первой из которых
использованы конечные разности yi, 2yi и 3yi, а во второй – коэффициенты a0, a1, a2 и a3.
P3(Х)=Y0+ yi(X-X0)/h+ 2yi(X-X0)(X-X1)/(2!h2) + 3yi(X-X0)(X-X1)(X-X2)/(3!*h3)
4 |
Любимов Е.Б. |
|
и
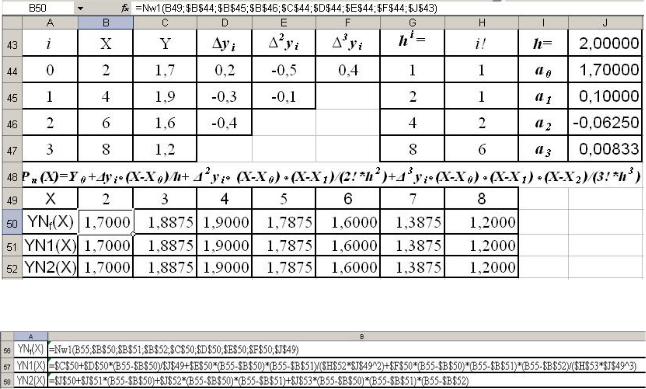
P3(Х)= a0+ a1 (X-X0) + a2 (X-X0)(X-X1)+ a3 (X-X0)(X-X1)(X-X2)
Полученные результаты (см. рис.8) подтверждают идентичность этих вариантов решения.
В строке формул на этом рисунке записано обращение к функции пользователя Nw1(), текст которой приведён ниже.
На рис.9 приведены три варианта формул, записанных в ячейки первого столбца для вычисления значений многочлена Ньютона в точке Х0.
Рис.8. Результаты вычислений по формуле Ньютона для трёх вариантов реализации
Рис.9. Варианты обращений при вычислениях по формуле Ньютона для трёх реализации
Формулы, записанные в столбец В таблицы протягиваются по строкам до столбца Н, обеспечивая вычисление значений интерполяционного полинома.
Окончательные результаты вычислений, оформленные в виде таблицы и диаграммы приведены на рис. 10.
На рис.11 и рис.12 приведены страницы отчёта по лабораторной работе, подготовленные для вывода на печать.
5 |
Любимов Е.Б. |
|
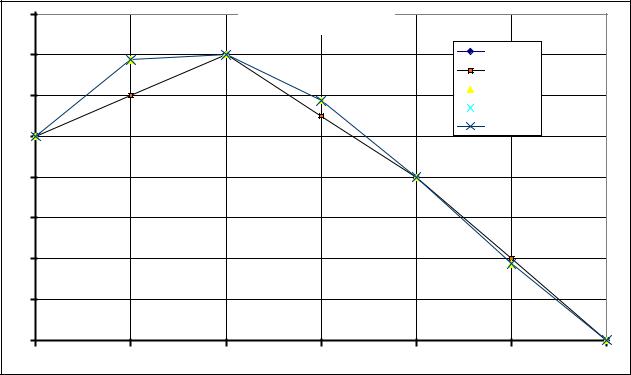
Сводная таблица результатов интерполяции
X |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Yисходн |
1,7000 |
|
1,9000 |
|
1,6000 |
|
1,2000 |
YЛ(X) |
1,7000 |
1,8000 |
1,9000 |
1,7500 |
1,6000 |
1,4000 |
1,2000 |
YK(X) |
1,7000 |
1,8875 |
1,9000 |
1,7875 |
1,6000 |
1,3875 |
1,2000 |
YL(X) |
1,7000 |
1,8875 |
1,9000 |
1,7875 |
1,6000 |
1,3875 |
1,2000 |
YN(X) |
1,7000 |
1,8875 |
1,9000 |
1,7875 |
1,6000 |
1,3875 |
1,2000 |
2,0 |
|
|
Сводная диаграмма |
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
Yисходн |
|
||
1,9 |
|
1,8875 |
1,9000 |
|
|
||
|
|
|
|
YЛ(X) |
|
||
|
|
|
|
|
|
||
1,8 |
|
1,8000 |
1,7875 |
|
YK(X) |
|
|
|
|
YL(X) |
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1,7 |
1,7000 |
|
1,7500 |
|
YN(X) |
|
|
|
|
|
|
|
|||
1,6 |
|
|
|
|
1,6000 |
|
|
1,5 |
|
|
|
|
|
|
|
1,4 |
|
|
|
|
1,3875 |
1,4000 |
|
|
|
|
|
|
|
|
|
1,3 |
|
|
|
|
|
|
1,2000 |
1,2 |
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
|
Рис.10. Сводная таблица вычислений и объединённая диаграмма |
|
|||||
|
интерполяционных функций |
|
|
|
|
||
Текст функции, обеспечивающей вычисление значения интерполирующего полинома по формуле Ньютона.
Function Nw1(x, x0, x1, x2, Y0, d1, d2, d3, h)
'текущее значение аргумента х
'значения аргумента в узловых точках таблицы х0, х1, х2
'значения конечных разностей d0, d1,d2,d3
'h - шаг приращения аргумента х
Nw1 = Y0 + d1 * (x - x0) / h + d2 * (x - x0) * (x - x1) / (2 * h ^ 2) + d3 * (x - x0) * (x - x1) * (x - x2) / (6 * h ^ 3)
End Function
6 |
Любимов Е.Б. |
|
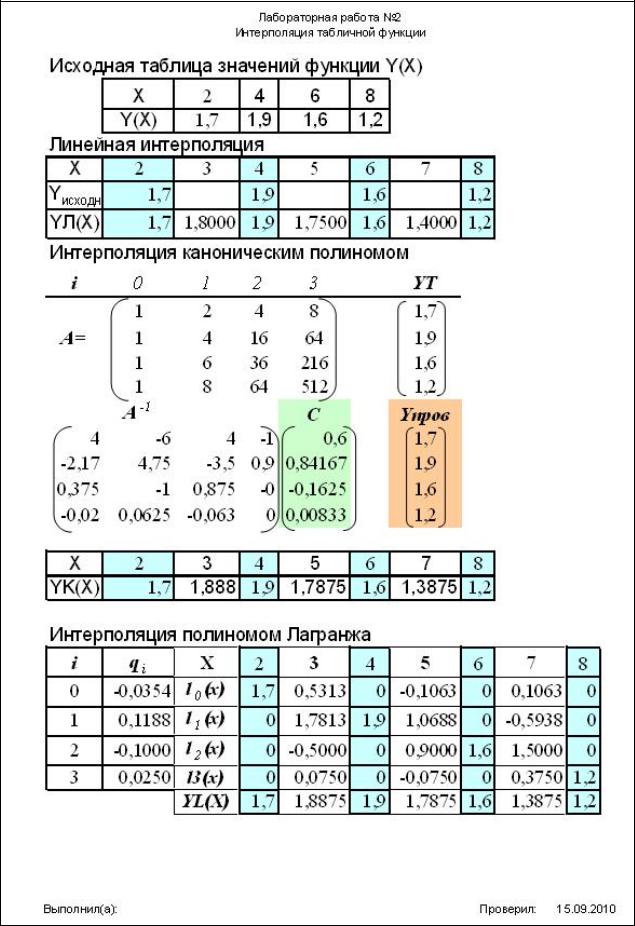
Рис.11. Первая страница отчёта (в режиме предварительного просмотра)
7 |
Любимов Е.Б. |
|
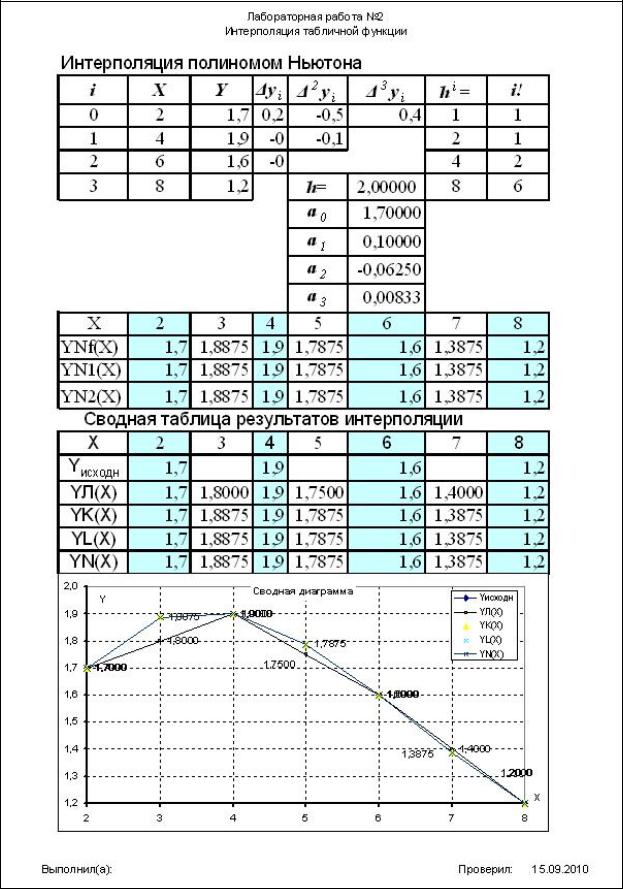
Рис.12 Вторая страница отчёта (в режиме предварительного просмотра)
8 |
Любимов Е.Б. |
|
Варианты индивидуальных заданий |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
№ варианта |
x1 |
x2 |
x3 |
x4 |
y1 |
y2 |
y3 |
|
y4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
-1 |
0 |
1 |
2 |
-3 |
5 |
2 |
|
3 |
||
|
2 |
2 |
3 |
4 |
5 |
4 |
1 |
7 |
|
6 |
|
|
3 |
0 |
2 |
4 |
6 |
-1 -4 |
2 |
-2 |
|||
|
4 |
7 |
9 |
11 |
13 |
2 |
|
-2 |
3 |
|
2 |
|
5 |
-3 -1 |
1 |
3 |
7 |
-1 |
4 |
|
3 |
||
|
6 |
1 |
2 |
3 |
4 |
-3 -7 |
2 |
|
3 |
||
|
7 |
-2 -1 |
0 |
1 |
4 |
9 |
1 |
|
1 |
||
|
8 |
2 |
4 |
6 |
8 |
9 |
|
-3 |
6 |
|
4 |
|
9 |
-4 -2 |
0 |
2 |
2 |
8 |
5 |
|
3 |
||
|
10 |
-1 |
1 |
3 |
5 |
4 -7 |
1 -2 |
||||
|
11 |
2 |
4 |
6 |
8 |
-1 -6 |
3 |
|
4 |
||
|
12 |
-9 -7 -5 -3 |
3 -3 |
4 -4 |
|||||||
|
13 |
0 |
1 |
2 |
3 |
7 |
|
-1 |
8 |
|
0 |
|
14 |
-8 -5 -2 |
1 |
9 |
-2 |
4 |
|
2 |
|||
|
15 |
-7 -5 -3 -1 |
4 |
-4 |
5 |
|
2 |
||||
|
16 |
1 |
4 |
7 |
10 |
-2 |
|
9 |
3 |
|
0,5 |
|
17 |
7 |
8 |
9 |
10 |
6 |
|
-2 |
7 |
|
0 |
|
18 |
-4 |
0 |
4 |
8 |
4 |
|
8 -2 |
|
2 |
|
|
19 |
-3 -1 |
1 |
3 |
11 -1 |
6 |
|
4 |
|||
|
20 |
0 |
3 |
6 |
9 |
1 |
|
5 -4 -2 |
|||
|
21 |
0,7 |
0,8 |
0,9 |
1,0 |
0,7 |
1 |
6 |
|
11 |
|
|
22 |
2,7 |
2,75 |
2,8 |
2,85 |
0,7 |
0,8 |
0,95 |
1,2 |
||
|
23 |
3 |
3,5 |
4 |
4,5 |
1,7 |
1,8 |
1,6 |
1,4 |
||
|
24 |
10 |
14 |
18 |
22 |
9,8 |
9,7 |
9,4 |
8,5 |
||
|
25 |
2 |
4 |
6 |
8 |
2,2 |
4,2 |
5,1 |
1,9 |
||
Оглавление |
|
"Интерполяция таблично заданных функций"....................................... |
1 |
Порядок выполнения вычислений........................................................... |
1 |
Инструкция по выполнению лабораторной работы на ЭВМ................ |
2 |
Текст функции Nw1(), обеспечивающей вычисление значения |
|
интерполируемого полинома по формуле Ньютона.............................. |
6 |
Оглавление ................................................................................................ |
9 |
9 |
Любимов Е.Б. |
|
