Примеры решения задач

1.2.1. Расчет статически неопределимого составного стержня, работающего на растяжение-сжатие (задача № 4) Условие задачи

Рис. 1.8. Схема нагрузки на стержень

в задаче № 4

Стержень переменного сечения с заданным соотношением площадей поперечного сечения, выполненный из разного материала, загружен силойF(рис. 1.8). Между правым концом стержня и стенкой существует зазор.

Требуется:

1. определить продольные силы, напряжения на каждом участке и проверить прочность стержня от действия заданной нагрузки F.

2. найти дополнительные напряжения, возникающие в стержне при его нагревании на температуру и проверить прочность стержня от температурного воздействия.

Решение

1. Определение напряжений от заданной нагрузки

Прежде всего надо убедиться, что заданная система является статически неопределимой. Найдем абсолютную деформацию стержня, показанного на рис. 1.8, предполагая сначала, что правая стенка отсутствует. Тогда, используя метод сечений, определим продольные силы на трех участках стержня:

на первом участке длиной ;

на втором и третьем участках .

Полное удлинение стержня, равное в общем случае , в данной задаче равно удлинению первого участка и, следовательно, по (1.3)

.

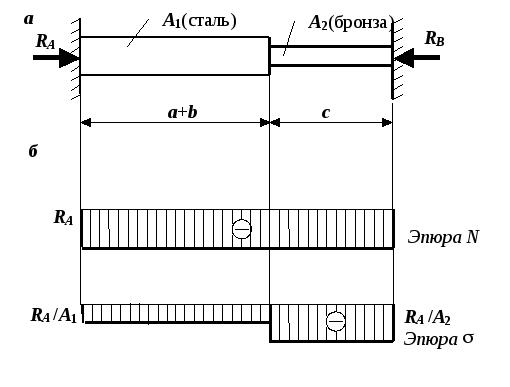
Рис. 1.9. К решению задачи № 4:

а – план сил от действия F,

б – эпюры продольной силы и напряжений от F

Если под действием нагрузки абсолютная деформациястержня будет больше заданного зазора, то стержень упрется правым концом в стенку и возникнут опорные реакции как в левом защемлении (), так и в правом опорном закреплении () (рис. 1.9,а). Для заданной системы можно составить только одно независимое уравнение статики. Таким образом, две неизвестные опорные реакции нельзя найти из одного уравнения, и система в процессе деформации становится один раз статически неопределимой.

Для раскрытия статической неопределимости используем расчет по упругой стадии деформаций и запишем три группы уравнений:

1. уравнения равновесия. Из них получим:

• для всего стержня ;

• для отсеченных частей стержня Заметим, что при составлении уравнений равновесия отсеченных частей стержня сделано предположение, что первая и вторая части стержня растянуты, а третья часть – сжата;

2. уравнение совместности деформаций, смысл которого в данной задаче очень простой: полная деформация стержня равна заданному зазору. При составлении уравнения совместности деформаций важно, чтобы знаки абсолютных деформаций соответствовали сделанным предположениям о направлении усилий. В нашем примере ;

3. физические уравнения

.

Решив полученную систему уравнений, найдем продольные силы, а затем напряжения в разных частях стержня и построим эпюры их распределения по длине стержня (рис. 1.9, б). Если знак усилия после решения системы уравнений получился отрицательным, это означает, что сделанное предположение о направлении продольной силы не подтвердилось. В рассмотренной задаче отрицательным должно получиться усилие, т. е. второй участок длинойb не растянут, а сжат. ЗнакиNина эпюрах ставим в соответствии с правилом знаков для продольной силы.

После определения напряжений производим проверку прочности по формулам (1.5) или (1.7) так же, как в статически определимой системе. Если условие прочности на каком-нибудь участке стержня не будет выполняться, измените значение Fтак, чтобы условие прочности соблюдалось.

2. Определение температурных напряжений

Найдем удлинение стержня от температурного воздействия и убедимся в том, что это удлинение больше заданного зазора.

.

Рис. 1.10. К решению задачи № 4: а – план сил от действия ,

б – эпюры продольной силы и напряжений от

Если>, то система является один раз статически неопределимой и раскрытие статической неопределимости производим по той же схеме, что и в предыдущей части задачи:

Из уравнений равновесия следует, что и. Здесь в соответствии с рис. 1.10,апредполагаем, что стержень всюду сжат. (СилуF при определении температурных напряжений считаем равной нулю.)

Уравнение совместности деформации показывает, что абсолютная деформация стержня, равная разности удлинения стержня от температурного воздействияи укорочения от действия сжимающих продольных силне может быть больше заданного зазора:

,

где .

Укорочение стержня от действия продольных сил найдем, используя физические уравнения (закон Гука):

и.

После решения полученной системы уравнений найдем усилия в обеих частях стержня. Полученный положительный знак должен подтвердить предположение о том, что стержень сжат. Строим эпюры продольной силы и напряжений (рис. 1.10, б) от температурного воздействия.

Проверяем прочность стержня и в случае невыполнения условия прочности на каком-нибудь участке находим новое значение , при котором условие прочности будет соблюдаться на всех участках.