Вариант 4
Написать уравнение прямой, проходящей через точку А (5; 2)
на расстоянии 4 единиц от точки (-3; 1).
2. В прямоугольном равнобедренном треугольнике даны: уравнение
катета
и середины гипотенузы (4; 2). Найти уравнения
других
сторон.
Найти биссектрисы углов между прямыми
и
.Привести к каноническому виду и построить:
а)
;
б)
;
в)
Найти расстояние от левого фокуса
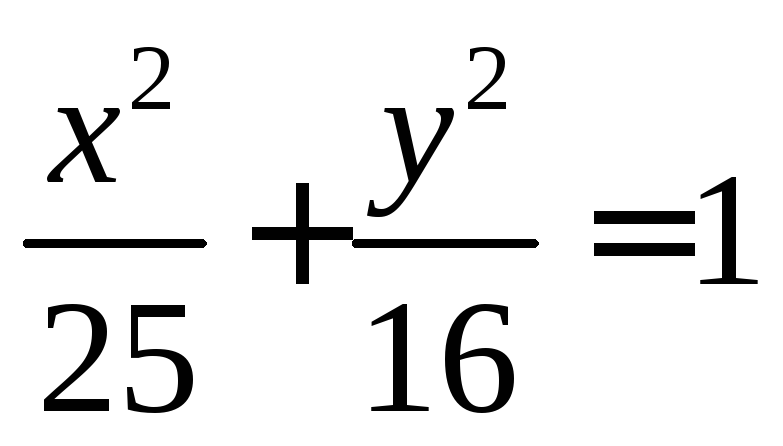до центра окружности
.
Через вершину параболы
провести прямые
параллельные
асимптотам гиперболы
7. Найти скалярное
и векторное
произведения
векторов. Координаты точек А (0; 1; 1), В (2; 1; 0), С (-1;5; 6)
заданы в декартовой системе координат.
Доказать параллельность прямых:
,
,
и
9. Дана плоскость
и вне ее точка М (1; 1; 1).
Найти точку P, симметричную точке М относительно данной
плоскости.
Написать уравнение плоскости, параллельной прямой
и прямой
проходящей через точку М (1; -1; 1).
Индивидуальное домашнее задание
по аналитической геометрии и векторной алгебре
Вариант 5
1. Найти внутренние
углы треугольника, если даны уравнения
его сторон АВ:
;
АС:
и основание Д (-1; 3)
высоты АД.
2. Стороны
параллелограмма заданы уравнениями
и
,
диагонали его пересекаются в точке (1;
4). Найти длины
его высот.
3. Две стороны
параллелограмма заданы уравнениями
и
.
Диагонали его пересекаются в начале
координат.
Написать уравнения его двух других сторон и диагоналей
параллелограмма.
4. Привести к каноническому виду и построить:
а)
;
б)
;
в)
.
5. Найти каноническое уравнение гиперболы, если ее асимптоты
заданы
уравнениями
,
а один из фокусов находится в точке
(-13;0).
6. Найти уравнение прямой, проходящей через фокус параболы
параллельно
прямой, соединяющей левый фокус
и нижнюю вершину
эллипса
.
7. Найти скалярное
и векторное
произведения
векторов. Координаты точек А (1; 1; -1), В (2; 1; 0), С (1; 2; 1)
заданы в декартовой системе координат.
8.Найти угол между
прямой
и плоскостью
.
9. Написать уравнение прямой, параллельной прямой
и проходящей
через точку пересечения прямых
и
.
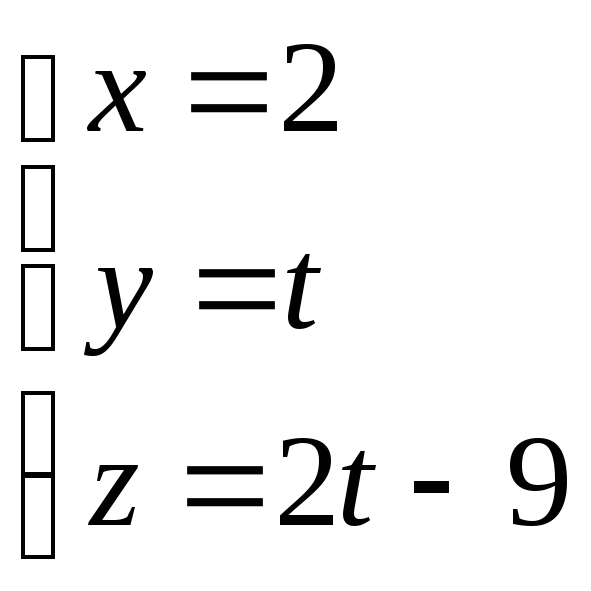Написать уравнение плоскости, проходящей через три точки
А (2; -1; 3); В (-1;0;2); С (-2; 1; 3).
Индивидуальное домашнее задание
по аналитической геометрии и векторной алгебре
Вариант 6
Уравнения двух сторон параллелограмма:
и
.
Центр его в точке (1; 2). Найти уравнение двух других сторон.
Через точку (0; 1) провести прямую так, чтобы ее отрезок,
заключенный между
двумя данными прямыми
и
,
делился в этой точке пополам.
Найти точку пересечения медиан равнобедренного треугольника, если даны уравнения боковых сторон
и
и точка (3; 8),
лежащая на основании.
Привести к каноническому виду и построить:
а)
;
б)
;
в)
.
5. Написать уравнение равнобочной гиперболы, один из фокусов
которой
совпадает с центром окружности
.
6. Вывести уравнение прямой, проходящей через фокус параболы
перпендикулярно
прямой, проходящей через левый
фокус эллипса
и центр окружности
.
7. Найти
скалярное
и векторное
произведения
векторов. Координаты точек А (3; 2; 1), В (1; 2; 3), С (0; 1; 2)
заданы в декартовой системе координат.
Найти проекцию точки Р (2; -1; 3) на плоскость
.
Составить уравнение плоскости, которая проходит через точку
М (3; -2; -7) параллельно
плоскости
10. Написать уравнение прямой, параллельной прямой
и проходящей через точку пересечения прямых
и
Индивидуальное домашнее задание
по аналитической геометрии и векторной алгебре