Сборник трудов конференции СПбГАСУ 2014 ч
.1.pdf





Раздел 3. Аналитические и численные методы исследований оснований и фундаментов
Задача 1. Подземный трубопровод левый конец защемлен, а правый конец свободен. Действует сейсмическая нагрузка, изменяющаяся во време-
ни u0 (t) Asin t .
Механические и геометрические параметры приняты в следующем ви-
де.
E 2 106 кГ/см2; |
|
F 2 R см2; |
0,5 см; |
DH 27 см; |
R 13,5 см; |
||||||||||||
8 10 6 кГс2/см4; |
|
|
m F кГс2/см2; |
T 0,05 с; |
|
l 10000 см; |
A 2 см; |
||||||||||
|
|
|
|
T |
|
|
2 |
|
|
t t |
|
|
(t) |
|
|
|
|
3 |
|
|
с; |
|
|
при u |
0 |
. |
|
|
|||||||
kx 2,5 кГ/см ; t0 |
2 |
T |
. u0 (t) |
|
|
при 0 |
|
|
|
||||||||
|
|
|
|
|
|
|
t t0 |
|
|
|
|
||||||
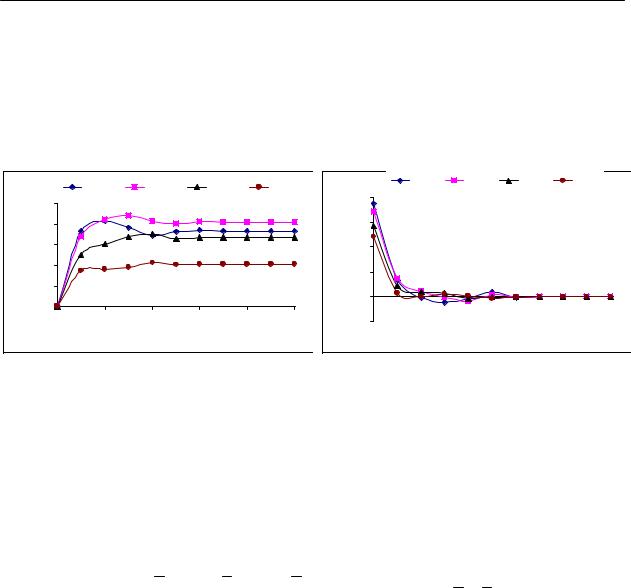
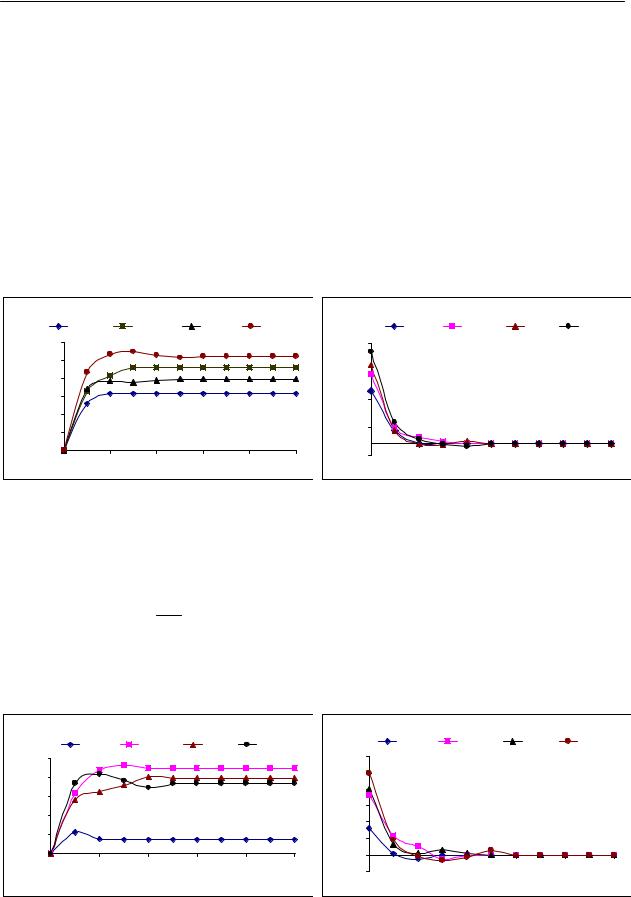
Результатырешениякраевойзадачиприводитсяввидеграфикарис. 1 и 2.
|
|
|
|
|
u0=Asinωt |
|
|
|
|
|
|
|
|
u0=Asinωt |
|
|
|
|
||
|
|
|
|
t=0.0015 |
t=0.00225 |
|
t=0.003 |
|
t=0.00375 |
|
|
t=0.0015 |
t=0.00225 |
|
t=0.003 |
t=0.00375 |
|
|||
|
|
0,06 |
|
u, см |
|
|
|
|
|
|
|
|
|
180 |
σ, кГ/см2 |
|
|
|
|
|
|
|
0,05 |
|
|
|
|
|
|
|
|
|
|
|
130 |
|
|
|
|
|
|
|
|
0,04 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,03 |
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
0,02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,01 |
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x, |
||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
x, |
-20 0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
20 |
40 |
60 |
80 |
100 |
|
|||
|
|
|
0 |
20 |
40 |
60 |
|
|
80 |
100 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рис. 1. Изменение перемещения по длине |
|
Рис. 2. Изменение напряжения по длине |
|
|||||||||||||||||
|
|
|
|
трубопровода |
|
|
|
|
|
|
|
трубопровода |
|
|
|
|||||
|
|
Задача 2. Подземный трубопровод левый конец защемлен, а правый |
||||||||||||||||||
конец свободен. Действует сейсмическая нагрузка изменяющая по закону |
||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
(x,t) |
|
|
|
|
C |
|
50000 см/с, остальные исходные данные при- |
|||||||||||
0 |
Asin t |
|
|
p |
||||||||||||||||
|
|
|
|
|
C p |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
няты как в задаче 1. Результаты решения краевой задачи приводится в виде |
||||||||||||||||||||
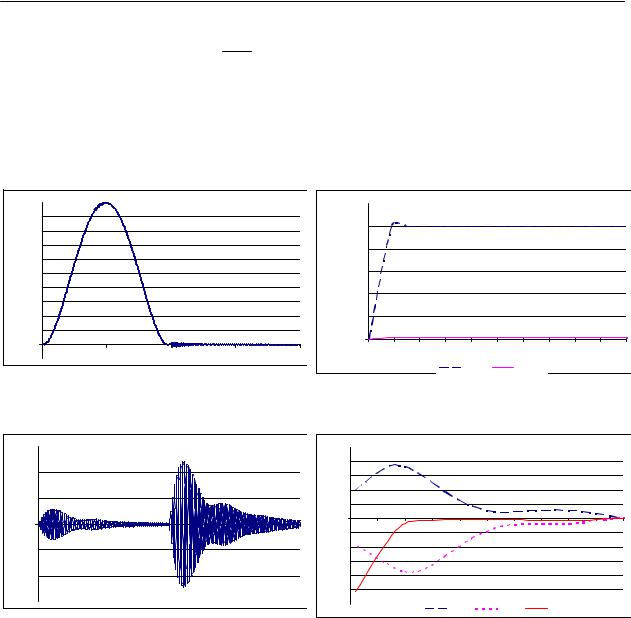
графика рис. 3 и 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
u0=Asinω(t-x/cp) |
|
|
|
|
|
|
|
u0=Asinω(t-x/cp) |
|
|
|
|||||
|
|
|
|
t=0.0015 |
t=0.00225 |
|
t=0.003 |
|
t=0.00375 |
|
|
t=0.0015 |
t=0.00225 |
|
t=0.003 |
t=0.00375 |
|
|||
|
|
|
|
|
|
|
180 σ, кГ/см2 |
|
|
|
|
|
||||||||
|
|
0,05 u, см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
0,04 |
|
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,03 |
|
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90 |
|
|
|
|
|
|
|
|
|
0,02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,01 |
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
100x, |
0 |
|
|
|
|
|
x, |
|
|
|
0 |
|
20 |
40 |
|
60 |
|
|
|
80 |
-30 0 |
20 |
40 |
60 |
80 |
100 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рис. 3. Изменение перемещения по длине |
|
Рис. 4. Изменение напряжения по длине |
|
|||||||||||||||||
|
|
|
|
трубопровода |
|
|
|
|
|
|
|
трубопровода |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
577 |
|
|
|
|
|
|
|
|