Сборник трудов конференции СПбГАСУ 2014 ч

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

12 % и более, особенно при залегании более плотных грунтов в верхней части сжимаемой толщи и практически исключить неравномерность осадки. Следствием чего является также отсутствие перераспределения усилий в надземных конструкциях.

2. Для достижения заданного распределения контактных давлений на основание необходимо создание фундаментов обладающих свойством управляемого взаимодействия с грунтовым основанием, чего можно добиться определенными конструктивными и технологическими приемами.

Таким образом, идея о контролируемом взаимодействии системы "фундамент – грунтовое основание" нуждается в дальнейшем развитии и совершенствовании методик ее применения.

в сплошную плиту переменной жесткости с предварительным напряжением грунтового основания: Автореф. дис. канд. техн. наук. — Тюмень, 2013. —24 с.

3.Пронозин Я.А., Бартоломей Л.А., Соколов В.Г., Отраснова Е.С. Расчетное обоснование степени неравномерности нагружения в целях снижения глубины сжимаемой толщи // Современные проблемы науки и образования. – 2013. – № 4; URL: www.science- education.ru/110-9545 (дата обращения: 01.11.2013).

4.Пронозин Я.А., Мельников Р.В. Расчет взаимодействия осесимметричных фун- даментов-оболочек с глинистым основанием // Научно-технический журнал «Вестник МГСУ».- 2011.-№7.- С. 577-584.

5.Пронозин Я.А., Порошин О.С., Степанов М.А. Применение ленточных фундаментов мелкого заложения, объединенных пологими оболочками, на сильносжимаемых грунтовых основаниях // Инновационные конструкции и технологии в фундаментостроении и геотехнике: материалы науч.-тех. конф. с междунар. участием (27-29 окт. 2013 г.). –

М., 2013. – С. 110-117.

6.СП 50-13330-2011. «Основания зданий и сооружений».- М.: Минрегион России,

2010.

7.Тетиор А.Н. Фундаменты: учеб. пособие для студ. учреждений высш. проф. образования/ А.Н. Тетиор . – М.: Издательский центр "Академия", 2010 – С. 126-128.

8.Чикишев В.М., Пронозин Я.А., Миронов В.В. К вопросу о деформируемости грунтового основания при равномерном и неравномерном нагружении // Интернетвестник ВогГАСУ. Сер.: политематическая, 2012. Вып. 1 (20).

561

Современные геотехнологии в строительстве и их научно-техническое сопровождение

УДК 624.131

Б.И. Кулачкин, А.А. Митькин, Д.Д. Шмидт

(ООО ИПТС-«Транспроект», Москва, РФ;

ООО «ТрансКапСтрой», Москва, РФ)

НЕКОТОРЫЕ ДИСКУССИОННЫЕ ПРОБЛЕМЫ ГЕОТЕХНИКИ И МЕХАНИКИ ГРУНТА

Новая модель «Геомассив – основание – фундамент – сооружение». Эта модель существенно расширяет область применения традиционной модели «основание – фундамент – сооружение» как в части механики грунта, так и в окружающей среде. Наиболее ярко новая модель проявляет себя в транспортном строительстве, когда имеют место линейнопротяженные сооружения (мосты, путепроводы и др). В частности, эта модель рассматривает каждую опору большого и среднего моста как отдельное сооружение (1,2). Проектировщики и строители широко используют модель «Геомассив – основание – фундамент – сооружение». «ТрансКапСтрой» использует эту модель на всех объектах более 8 лет.

При строительстве моста через р. Ликова (Московский регион) основание одной из опор содержало реликтовый врез, который в процессе инженер- но-геологических изысканий не был обнаружен и существенно снижал прочность основания (3). В результате пришлось вносить изменения в проект.

При строительстве монорельсовой дороги в г. Москва в процессе строительства двух опор обнаружились большие осадки. После изучения причин больших осадок оказалось, что недалеко, на расстоянии около 60 м производилось водопонижение, а поскольку основание опор было песчаным, то возникли дополнительные осадки.

Еще один яркий пример. Мостовой переход через р. Волга у с. Пристанное длиной более 20 км. Рассматривать проект или его часть без модели «геомассив – основание – фундамент – сооружение» практически невозможно.

Модель «Геомассив – основание – фундамент – сооружение» имеет широкие возможности для своего развития в отношении окружающей среды, когда природные условия и технология существенно влияют на проекты в части геотехники (4). Здесь следует отметить широко используемый за рубежом Observation Method в геотехнике окружающей среды (5). В качестве примера применения данного метода в геотехнике можно привести коррекцию проекта на развязке Дмитровского шоссе в Москве, когда была произведена замена забивных свай на буронабивные по ряду экологических и геотехнических причин (6).

Аналого-дискретная модель грунта. Все известные модели грунта, широко используемые в механике грунта – аналоговые (непрерывные). На самом деле грунт – аналого-дискретная среда (7, 8, 9, 10). Наиболее ярким представителем такой среды является просадочный грунт.

562

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

Процесс просадки грунта очень сложно контролировать в строительной практике. И хотя предпринимается много различного рода попыток описать этот процесс аналитически, на основе непрерывных функций, результат нельзя признать положительным (8). В том, что грунт, основание, геомассив являются аналого-дискретной средой, можно легко убедиться, посмотрев на диаграммы статического зондирования (аналоговая регистрация) в различных источниках (9, 10).

Если рассматривать с общих позиций механики, то все известные модели грунта, а также др. строительных материалов (сталь, бетон, полимер

идр.) основаны на 3-х идеальных телах*: Гук (Н) – упругость, Ньютон (N) – вязкость, и Сен-Венан (Stv) – сухое трение в их различных сочетаниях и интерпретациях, и, естественно, являются аналоговыми (непрерывными), но что касается грунта, то он вполне укладывается (современные научные предсавления) в рамки теории предельного равновесия и др. На первый взгляд это действительно так. Вместе с тем исследования, выполненные в 80-х годах прошлого века и позднее, включая зондирование, показали, что это совсем не так (11, 12). Именно зондирование и в общем глубокое исследование измерительных систем (13) позволило получить эти принципиально новые результаты (14, 15, 16). Существо этих результатов заключается в следующем. Практически все статические процессы заканчиваются измерением некоего конкретного значения перемещения (деформации), нагрузки (напряжение, давление).

Что касается динамики, анализа и соотношения инерционных характеристик объекта исследования и измерительной системы не было ни в РФ ни за рубежом. Необходимое соотношение было реализовано в измерительных системах для статического зондирования (1, 2). Это позволило обнаружить дискретность грунта во всем диапазоне нагрузок, начиная даже практически с 0. Таким образом, на базе практически «безинерционных» измерительных систем по отношению к грунту, получена новая информация о прочности грунта в широком понимании этого термина. В дополнение к идеальным аналоговым телам N, H и Stv добавлено идеальное хрупкое тело «КулачкинРадкевич» (KR) (17, 18), которое, с нашей точки зрения, в полной мере решает вопрос поведения грунта под нагрузкой во всем диапазоне, но это касается также всех материалов (сталь, бетон, полимер и др).

Идеальная аналого-дискретная модель может быть представлена состоящей из четырех идеальных тел: N (Ньютон), H (Гук), Stv (Сен-Венан)

иKR (Кулачкин-Радкевич). Простейшая схема модели представлена на рис. 1.

*Если иметь в виду реальные модели грунта, то они наделены различного рода свойствами, полученными экспериментальным путем.

563

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Реальные модели существенно до-

Nполняют и усложняют идеальную модель. Идеальная аналого-дискретная модель на основе четырех идеальных

KR H N Stv и др. Безусловно, на основе экспериментальных исследований получено очень много побочных свойств, которые информационно обогащают грунт и, конечно, модели. К примеру, новую модель с параметром просадки возможно рекомендовать для практического применения в просадочном грунте.

Эффект «Кулачкина-Радкевича» (19, 20). Этот эффект позволил в ка- кой-то степени обнаружить аномальное явление. Поровое давление внутри песчаной насыпи, образованной гидронамывом (строительство мостового перехода в г. Саратове через р. Волга у села Пристанное), оказалось меньше атмосферного (!)

Этот результат был получен благодаря новой методике измерений порового давления в процессе статического зондирования. В данном случае проводилось измерение порового давления в процессе его релаксации при остановке зонда. Эта методика принципиально отличается от рекомендуемой, изложенной в международном стандарте на СРТ.

Витоге оказалось, что поровое давление внутри песчаной насыпи являлось неким стабилизирующим фактором, что повысило устойчивость песчаной насыпи. Этот эффект важен для понимания процессов, происходящих в массиве грунта как при техногенном воздействии, так и при эволюции верхних слоев литосферы.

Капиллярная модель грунта. Высота капиллярного поднятия, капиллярные силы и их учет в различного рода расчетах имеют важное значение в геотехнике. В нормах РФ в достаточно общем виде обозначены высоты капиллярного поднятия для различных видов грунта. Проведенные исследования в различных регионах РФ, в том числе с использованием ННК (нейтроннейтронный каротаж) и ГК (гамма-гамма каротаж) показали, что высота капиллярного поднятия нестабильна и не достигает величины более 2 м (21).

Впроцессе эволюции или техногенеза могут образовываться как традицион-

564

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

ные капилляры так и капилляры Жомена (11). На этой основе разработана комбинированная капиллярная модель.

Одним из главных выводов этой модели является отсутствие прямой связи между высотой и силой капиллярного поднятия (тем более, что объемная и весовая влажности по высоте каймы капиллярного поднятия нестабильны и сама кайма неровная).

Экспериментальные исследования проводились в различных регионах РФ. Большое количество исследований выполнялось в Узбекистане. Разработанная комбинированная модель показывает, что больших высот капиллярное поднятие не достигает, хотя в одной из своих работ К. Терцаги допускал, что высота капиллярного поднятия может достигать более 100 м.

Поровое давление. Вопрос с поровым давлением был решен в большой степени в рамках открытия №186 (22) «Закономерность распределения порового давления в глинистых породах». Это открытие позволяет рассматривать поровое давление как элемент памяти образования и эволюции верхних слоев литосферы. Здесь следует отметить, что вслед за этим открытием последовало много научных работ о некоей памяти воды и больших возможностях методики её оценки. Исследования показали (1, 2, 22, 23), что в водонасыщенных песках (открытый геомассив) поровое давление в полной мере соответствует гидростатическому давлению. В глинистой породе (24, 25) поровое давление распределено неравномерно и может быть меньше гидростатического, равно гидростатическому, больше гидростатического, вплоть до литостатического давления (26). В качестве такого примера можно привести измерение порового давления в неоднородном геомассиве в одном из районов Таллина. Здесь не рассматривается вопрос аномально высоких пластовых давлений. Широкое применение методики измерения порового давления было основано на применении прибора «ПИКА» (24, 27, 28, 29, 30).

Классификация грунта. Известно, что К. Терцаги и Р. Пек ввели понятие переуплотненного грунта. Однако долгое время в РФ переуплотненный грунт как категория не фигурировал. В конце 20 века Б.И. Кулачкиным была введена новая классификация грунта: переуплотненный – нормальноуплотненный – недоуплотненный грунт. Переуплотненный грунт был введен

вМГСН-2003. Практическое использование этой классификации позволило обосновать возможность надстройки существующих зданий и сооружений,

вчастности, в Москве. Использование этой классификации было осуществлено при проектировании и строительстве автодороги «Шантала – Клявлино»

вСамарской обл. и при строительстве магистрали Север-Юг в Израиле. Природное давление. Природное давление, которое представляется как

h, не в полной мере отражает суть вопроса. Так, С.Б. Ухов и его коллеги (31) пишут, что это сложный с инженерной точки зрения вопрос. Природное давление, во всяком случае на небольших глубинах, зависит от эволюции верхних слоев литосферы.

565

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Чтобы каким-то образом прояснить этот вопрос, проведен ряд исследований. Стало ясно, что определение природного (бытового) давления не может быть решено аналитически. Кстати, этот вопрос неким образом связан с классификацией грунта (переуплотненный, нормальноуплотненный и недоуплотненный грунт). Были предприняты попытки оценить природное (бытовое) давление через боковое давление. Был сконструирован зонд (32) для статического зондирования с измерением бокового давления, причем в конструкции предусмотрена компенсация от различного рода погрешностей. Эксперименты показали, что природное (бытовое) давление может быть экспериментально определено в необходимых случаях, что существенно уточняет различного рода расчеты. Особенно это важно для оценки устойчивости склонов и откосов, когда сюда добавляется значение коэффициента по надежности нагрузки от собственного веса грунта.

Литература

1.Б.И. Кулачкин, А.И. Радкевич, А.Д. Соколов. Проблемы и перспективы геотехники. М., РАЕН, 2003.

2.Б.И. Кулачкин, А.И. Радкевич, Ю.В. Александровский, Б.С. Остюков. Фундаментальные и прикладные проблемы геотехники. М., РАЕН, 1999.

3.В.И. Шмидт, Б.И. Кулачкин, А.И. Радкевич и др. Опыт проектирования моста через р. Ликова. Вестник мостостроения №3-4, 2004.

4.Б.И. Кулачкин, А.И. Радкевич, Ю.В. Александровский, Б.С. Остюков. Основы строительной экологии. Саратов, изд. Саратовского университета, 2000.

5.N.R. Morgenstern. The Observation Method in Environmental Geotechnics. Proceedings of the First International Congress on Environmental Geotechnics. Edmonton. Canada, 1994.

6.Д.Д. Шмидт. Концепция исследования качества искусственных сооружений в условиях Москвы. Транспортное строительство №5, 2013.

7.И.И. Кондрауров. Теория дискретного распределения вертикальных напряжений

идеформаций сжатия в однородных и слабых грунтовых основаниях. Всесоюзный съезд по теоретической и прикладной механике. А Н СССР, 1960.

8.В.И. Крутов, А.С. Ковалев, В.А. Ковалев. Проектирование и устройство оснований и фундаментов на просадочных грунтах. М., Изд. АСВ, 2013.

9.В.А. Ильичев, Б.И. Кулачкин, A.P. Van den Berg и др. Советско-голландский эксперимент в области зондирования грунтов. Основания, фундаменты и механика грунтов. 1986, №5.

10.Б.И. Кулачкин. Исследование метода зондирования для определения относительной просадочности и коэффициента фильтрации лессовых грунтов. Авт.диссертации на соискание уч.ст. к.т.н. М., НИИОСП, 1975.

11.Б.И. Кулачкин. Экспериментальнотеоретические исследования и разработка метода зондирования в инженерной геологии. Авт.диссертации на соискание уч.ст. д.г.-м.н. Ташкент, 1991.

12.B.I. Kulachkin, Yu.G. Trofimenkov, L.G. Mariupolsky, I.B. Rygkov. Cone Penetration Testing in Russia. Proceedings of the International Simposium on Cone Penetration Testing. Linkoping, Sweden, 1995.

13.Теория информации и ее практические приложения (сборник переводов) под ред.А.А. Харкевича. М., Изд.физ.-мат.лит., 1959.

566

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

14.B.I. Kulachkin, N.P. Betelev, V.P. Otrepiev, A.Z. Chister. Soil Classification by means of PIKA-10 Statik Penetration Tests. Proc. of the 1st Int. Symposium on Penetration Testing (ISOPT-1). Orlando, USA, 1988.

15.B.I. Kulachkin, A. Anand, A.I Radkevitch, N.P. Betelev. Soil Massives subdivision into Types of Soil. Proceedings of the Mongolian Geotechnic Conference MGC-96. Ulaanbaatar, Mongolia, 1996.

16. B.I. Kulachkin, A.I. Radkevitch, M.A. Trotsky, P.A. Schepetinov, I.P. Shlykov, J.G. Shakhgeldyan. Survey on Site of Port Salif in Yemen. Proceedings of the International Simposium on Cone Penetration Testing. Linkoping, Sweden, 1995.

17.Б.И. Кулачкин, А.И. Радкевич, В.И. Беда, Е.А. Гузеев, Д.А. Радкевич. Непрерывно (аналого)-дискретная модель грунта. Транспортное строительство №4, 2000.

18.Б.И. Кулачкин, А.И. Радкевич. Аналого-дискретная модель грунта. Международная научно-практическая конференция «Геотехника-99». Пенза, 1999.

19.Б.И. Кулачкин, А.И. Радкевич, Д.В. Паранин. Область пониженного давления внутри песчаной насыпи. Третья Украинская научно-техническая конференция по механике грунтов и фундаментостроению. Одесса, 1997.

20.Б.И. Кулачкин, А.И. Радкевич, В.И. Беда, Д.В. Паранин. Эффект КулачкинаРадкевича при возведении песчаной насыпи гидронамывом. 8-я Международная конференция по экспериментальным исследованиям инженерных сооружений, ЭИИС-98, 1998.

21.Б.И. Кулачкин. Капиллярная модель грунта. Рекламный листок. М., ВДНХ

СССР, 1979.

22.Б.И. Кулачкин, А.И. Радкевич, Ю.В. Александровский, Б.С. Остюков. Диплом №186. Научное открытие – Закономерность распределения порового давления в глинистых породах. М., РАЕН, 1991.

23.B.I. Dalmatov B.I. Kulachkin. Field Investigations Clay Soils. Proceedings of 10th Int. Conf. of Soil Mech. and Found. Eng.v.2, Rotterdam, 1981.

24.Б.И. Кулачкин. Поропьезометр – 1М. Паспорт НТД. М., НИИОСП, 1983.

25.Б.И. Кулачкин. Новая методика измерения порового давления. Паспорт НТД,

М., НИИОСП, 1984.

26.Б.И. Кулачкин, Н.П. Бетелев, А.З. Гинстер, В.П. Отрепьев. Измерение порового давления в грунтах зондированием. Библиографическая информация. Строительство и архитекткра. Выпуск 5, ВНИИИС, 1984.

27.Б.И. Кулачкин, Н.П. Бетелев, А.З. Гинстер, В.П. Отрепьев. Аномально высокие пластовые давления и средства их измерения. Библиографическая информация. Строительство и архитекткра. Выпуск 5, ВНИИИС, 1984.

28.Б.И. Кулачкин и др. Руководящий нормативный документ. Морские инженер- но-геологические изыскания. Определение строительных свойств донных грунтов комплектом ПИКА-10. Мингазпром, Баку, Гипроморнефтегаз, 1984.

29.Б.И. Кулачкин. Использование результатов статического зондирования для оценки физико-механических характеристик грунтов. Сб. №74. Основания, фундаменты и подземные сооружения. М., Стройиздат, 1984.

30.Б.И. Кулачкин, Н.П. Бетелев, В.П. Отрепьев, А.З. Гистер. Литологическое расчленение грунтовых массивов в Волгоградском Поволжье по результатам статического зондирования комплектом ПИКА-10. Инженерная геология №4, 1986.

31.С.Б. Ухов и др. Механика грунтов, основания и фундаменты. М., Высшая шко-

ла, 2007.

32.Б.И. Кулачкин и др. Устройство для определения физико-механических свойств грунта. А.С. №1191521 Бюл.№42, 1985.

567

Современные геотехнологии в строительстве и их научно-техническое сопровождение

УДК 627.4

М.С. Буняев (Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова)

РАСЧЕТ ГРУНТОНАПОЛНЯЕМЫХ ОБОЛОЧЕК, ПРИМЕНЯЕМЫХ В СТРОИТЕЛЬСТВЕ

Традиционные способы обеспечения надежности строительства за счет усиления конструкций фундаментов и увеличения их заглубления в значительной мере себя исчерпали, особенно на высокотемпературных льдистых пластичных грунтах. Одним из перспективных направлений в решении подобных проблем является использование оболочечных конструкций (водо-, воздухо-, грунтонаполняемых и т. п.) из композитных (полимерных) материалов, способных отражать внешнее воздействие на них применяя особенности трансформации начальной формы их перемещения под различными воздействиями (внутренних, внешних и т. п.), а также сохраняя ее [1].

Теорией мягких оболочек, занимались различные советские и зарубежные ученые, такие как С.А. Алексеев, В.П. Дыба [6], Б.И. Друзь, В.А. Волосухин, Л. Женевуа, В.Э. Магула [4], Т. П. Кашарина [2, 3], Ф.К. Лапшин, К.М. Хуберян, О.В. Шальнев [5] и др.

Несмотря на наличие упрощающего основные уравнения свойства безмоментности, построение теории мягких оболочек проблема очень сложная. Все осложняется тем обстоятельством, что мягкая оболочка под нагрузкой существенно изменяет геометрию. Это, в свою очередь, оказывает влияние на распределение нагрузки.

Одним из основных свойств мягких оболочек является их неспособность воспринимать сжимающие напряжения. Поэтому мягкая оболочка может находиться либо в двухосном напряженном состоянии, когда оба главных напряжения положительны, либо в одноосном, когда одно из главных напряжений пренебрежимо мало и его полагают равным нулю. В одноосной зоне оболочка не имеет определенной формы, поэтому нельзя произвольно задавать форму оболочки и действующие на неё нагрузки.

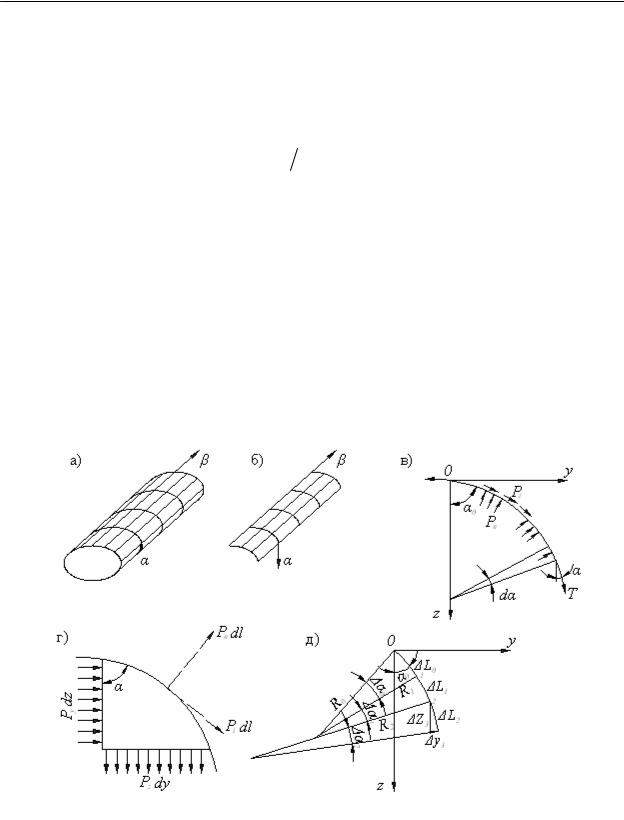
Рассмотрим оболочки плоского раскроя, принимающие под нагрузкой форму цилиндрических поверхностей (рис. 1, а, б). Такая идеализация допустима при плоском характере нагрузок, достаточном удалении рассматриваемых участков от торцов. Дифференциальная форма уравнений равновесия [4]:

где R – радиус кривизны сечения; Т=Т1 – кольцевое натяжение в оболочке. Линии α направлены ортогонально образующим, за α принят угол α (рис. 1, в). Проинтегрировав равенство (1) и подставив его в уравнение (2), находим

568

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

в цилиндрической мягкой оболочке постоянны по сечению (до линий действия сосредоточенных сил). При Р1=0, Рn=const, (из уравнения (164) R= const, т. е. сечение – дуга окружности. Когда Рn=0, Рn≠0 или Р1=0 R→∞, оболочка плоская.

Рис. 1. Цилиндрические оболочки под нагрузкой (плоская задача)

Уравнения равновесия в интегральной форме, т. е. в проекциях сил, приложенных к участку оболочки, на оси у и z:

569

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Так как при этом использовано одно из дифференциальных уравнений равновесия, для описания формы оболочки достаточно любого из тождественных равенств (8), (9).

Иногда нагрузка задана горизонтальной Ру и вертикальной Рz составляющими, отнесенными к единице длины перпендикулярной к ним координатной линии (рис. 1, г):

Рn cos2 (Py tg 2 Pz ) ; Р1 sin 2 Py Pz tg

Когда Р1=0, Ру = Рz = Рn (индексы «у» и «z» не означают дифференцирования).

При таких нагрузках вместо формул (3), (6) и (7) имеем

0

В оболочках градиент продольных усилий Т2 вдоль сечений α обычно невелик. Это позволяет при учете кольцевых деформаций λ1 либо считать

Т2(α)≈const, либо Т2(α)≈f(Т1) и λ1= λ1(Т, С1,…, Сn). В таком случае с учетом кольцевых деформаций число функциональных уравнений не увеличивается,

а дополняется граничным условием. Если Lo – длина дуги сечения в исходном состоянии, а L – в конечном, то

Величины α1, z1, L1 отвечают второй граничной образующей. Например, когда Т2=0,5Т и материал линейно-упругий,

570