Сборник трудов конференции СПбГАСУ 2014 ч

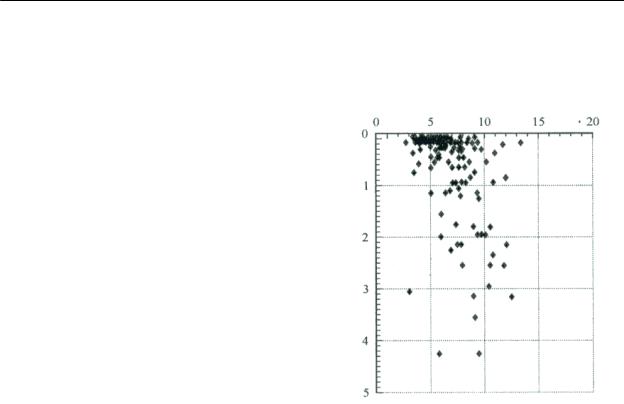
Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

сионного прибора и судового прибора чистого сдвига, разработанных на кафедре геотехники СПбГАСУ (ЛИСИ) с учетом низкой прочности и высокой деформативности образцов, а также защиты приборов от вибрации.

Число определений сопротивления грунта срезу крыльчаткой с габаритными размерами 25 30 мм и скоростью вращения образца 0,25 об/мин составило 857. Испытания проводились по схеме неконсолидированного среза с заданной скоростью деформирования образца. Установлено, что сопротивление грунта изменяется в достаточно широких пределах 1,8–17,4 кПа и имеет устойчивую тенденцию к увеличению с глубиной с градиентом 2 кПа/м (рис. 2) [3]. Обработка результатов испытаний методами математической статистики позво-лила сузить пределы прочности грунта до 4,4–6,8 кПа. Для оценки

достоверности набортных измерений сопротивления срезу проведено их сопоставление с аналогичными измерениями в естественном залегании, выполненных глубоководной крыльчаткой с размерами 75 100 мм при скорости вращения 1,0 об/мин. Расхождение между результатами определения сопротивления срезу на борту судна и в естественном залегании, которое составило 5,9–8,7 кПа, не превышает 22–26 %.

Зафиксированное снижение прочности донных грунтов на борту судна возможно объясняется нарушением природной структуры при отборе и подъеме образцов, снятием гидростатического давления, разными геометрическими размерами и скоростями вращения крыльчаток.

Для оценки зависимости сопротивления срезу глинистых грунтов от нормального напряжения на образцы прикладывалась нагрузка р равная 4, 6 и 8 кПа. Испытания проводились по схеме консолидированного-дрени- рованного кольцевого среза с постоянной скоростью деформирования образца. По данным семи измерений прочностных характеристик грунтов отмечено линейное увеличение сопротивления срезу с ростом вертикального давле-

ния. Угол внутреннего трения зафиксирован в пределах 6–10 , удельное сцепление изменяется от 1,3 до 5,2 кПа (рис. 3) [3].

531

Современные геотехнологии в строительстве и их научно-техническое сопровождение

, кПа

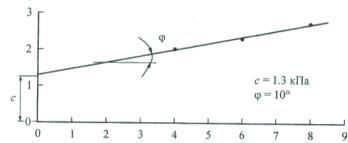p, кПа Рис.3. График сопротивления сдвигу образцов глинистого грунта [3]

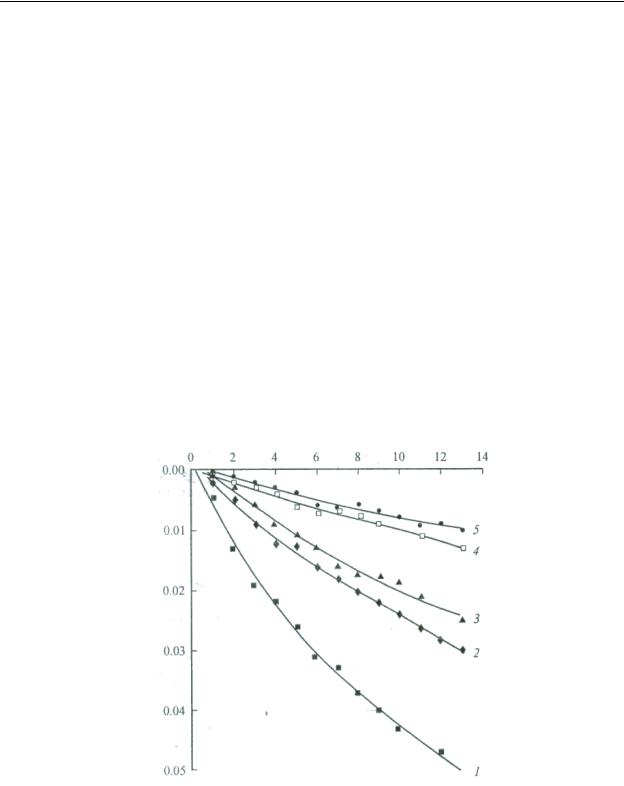
Испытание грунта методом компрессионного сжатия проводились для определения коэффициента относительной сжимаемости mv. Сжатие образца производилось при одностороннем дренировании. Число испытаний глинистых осадков составило 28. Диапазон давлений от 1 до 13 кПа со ступенями давления в 1кПа и их выдержкой 5 с, определялся в программе испытаний с учетом передаваемых на основание нагрузок от АС. Результаты испытаний оформленные в виде графиков зависимостей относительной деформации образца от давления p представлены на рис. 4 [3].

Давление, p кПа

Относительная деформация,

Рис.4. Зависимости относительной деформации грунта от давления при сжатии в судовом фильтрационно-компрессионном приборе:

1,2 глинистые осадки; 3 глина цеолитсодержащая; 4 глина радиоляриевая ; 5 глинисто-карбонатные отложения

Структурная прочность глинистых осадков (графики 1,2) находится в пределах 0,2–0,4 кПа. Зависимость = (р) близка к линейной. Наиболее

532

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

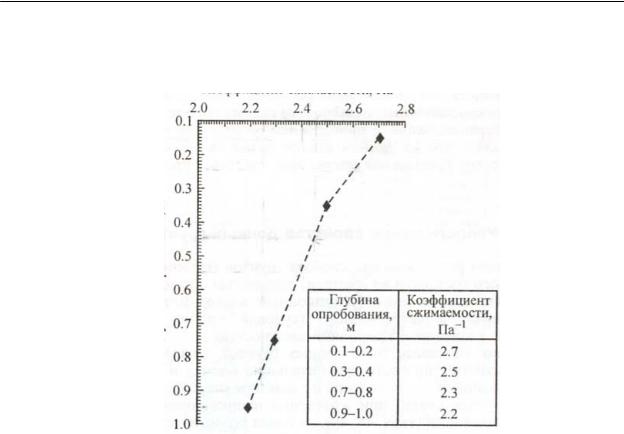
сжимаемы глинистые осадки у поверхности дна mv = 2,7 Па –1. Вниз по разрезу коэффициент сжимаемости несколько уменьшается (рис.5).

Коэффициент относительной сжимаемости, Па-1

Глубина опробования, м

Рис. 5. Изменение коэффициента сжимаемости по глубине [3]

Расчетная схема АС-основание

Несущим АС слоем служат слабые глинистые и кремнисто-глинистые осадки подстилающие ЖМК. Нагрузка на основание принимается гибкой, равномерно распределенной в пределах прямоугольника. Как показали экспериментальные исследования [4] приложение и снятие значительных гидростатических давлений к водонасыщенным донным осадкам не вызывают деформирования их скелета. В наиболее простой постановке деформирование полностью водонасыщенного грунта (грунтовой массы) при давлении превышающим структурную прочность грунта и не превышающим начальную критическую нагрузку описывает модель теории фильтрационной консолидации. Согласно этой модели происходит уплотнение грунта под действием внешней нагрузки. При этом часть воды из пор грунта, расположенного под подошвой АС, отжимается в наименее нагруженные области массива по закону ламинарной фильтрации Дарси. Скелет грунта рассматривается как упругая пористая среда, характеризуемая коэффициентом относительной сжимаемости mv. Любое приращение напряжений в скелете грунта мгновенно вызывает соответствующее приращение деформаций. Рассматривается ограниченный по времени процессом фильтрационной консолидации режим стоянка АС на дне.

533

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Расчет осадки АС

Размеры подошвы АС приняты равными: ширина b =1 м, длина l=5 м, давление по подошве p=7 кПа. Грунт основания текучепластичная глина IL=1, имеющая следующие параметры: угол внутреннего трения =0, удельное сцепление с=6 кПа, плотность =1,25 г/см3 (удельный вес=12,25 кН/м3), плотность частиц грунта s =2,6 г/см3 ( s =25,48 кН/м3), плотность воды w =1,05 г/см3 ( w =10,3 кН/м3), пористость n=0,86; коэффициент сжимаемости в зависимости от глубины mv = 0,0028 0,0022 кПа -1 (см. рис. 5).

Осадка основания определяется методом послойного суммирования.

Сжимаемая толща разбивается на слои толщиной 0,1 и 0,4 м. Сжатие элементарного слоя грунта принимается под действием равномерной нагрузки на его поверхности без возможности бокового расширения. Общая осадка АС находится как сумма величин сжатия каждого элементарного слоя в пределах сжимаемой толщи по формуле

i 1

где n число слоев в пределах сжимаемой толщи; hi толщина i-го слоя грунта; mvi относительный коэффициент сжимаемости i-го слоя грунта;zpi среднее значение дополнительного вертикального нормального напряжения в i-м слоя грунта.

Расчет осадки основания представлен в табл. 2.

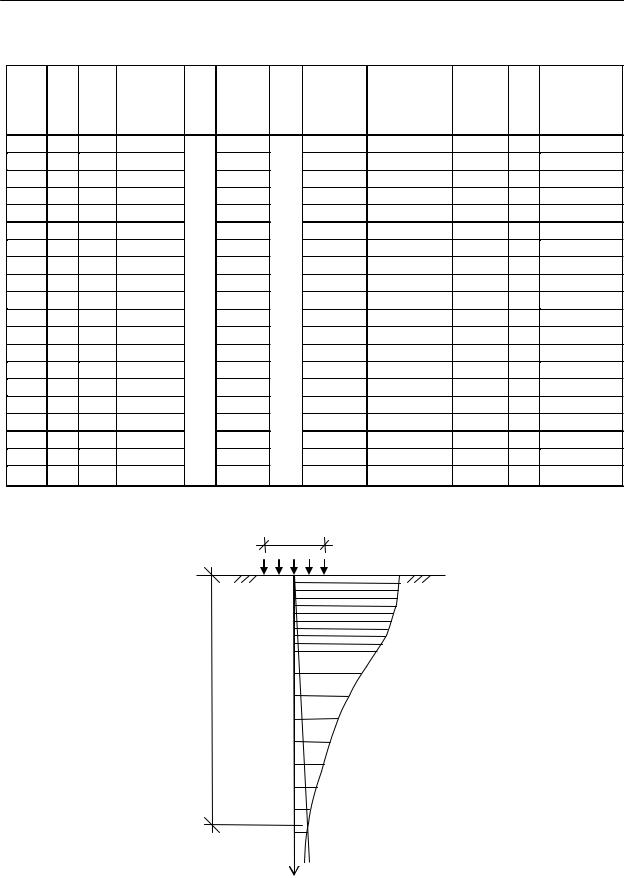
Нижняя граница сжимаемой толщи (рис. 6) назначается на глубине, где ордината эпюры дополнительных напряжений составляет 10 % от природного напряжения на этой же глубине [5].

Осадка АС s=2,46 см. Данный метод занижает осадку, так как не учитывает боковое расширение грунта.

Метод эквивалентного слоя приводит сложную пространственную задачу деформирования грунта к эквивалентной одномерной. Последний показывает хорошее совпадение с результатами натурных наблюдений при строительстве на слабых грунтах. Предварительно вычисляем: толщину эквивалентного слоя грунта

где A 0 коэффициент эквивалентного слоя для максимальной осадки гибкой нагрузки, принятый по таблице 50 [6] при соотношении сторон нагрузки l/b=5 и коэффициенте Пуассона =0,4. Конечная осадка основания АС равна

534

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

Рис. 6. Схема к определению глубины сжимаемой толщи грунта

535

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Для определения времени 95 % консолидации основания зададимся параметром N=2,8 и коэффициентом фильтрации донного грунта 2,13 10-5см/с [4].

Расчет времени консолидации представлен в табл. 3.

Таблица 3

Выводы

1.Глубоководный донный грунт можно считать двухкомпонентной системой (грунтовой массой), состоящей из минерального вещества, образующего скелет грунта, и поровой воды.

2.Для расчетов основания АС рекомендуется принять следующие фи- зико-механические характеристики донных грунтов, подстилающих ЖМК:

плотность =1,25 г/см3; плотность частиц грунта s=2,6 г/см3; плотность морской воды w=1,05 г/см3; пористость n=0,86; удельное сцепление грунта с=6,0 кПа; угол внутреннего трения =0; коэффициенты сжимаемости, изме- няющиесяпоглубинеmv=0,0028-0,0022 кПа; структурнаяпрочность str=0,2 кПа.

3. Осадка АС s=2,46 см, найденная методом послойного суммирования,

втриразаменьшеосадки, рассчитаннойметодомэквивалентногослоя, s=7,4 см. Расчетное время консолидации основания составляет 25,5 сут.

Литература

1.Минеральные ресурсы Мирового океана: концепция изучения и освоения (на период до 2020 г.). СПб.: ВНИИОкеангеология, 2007. 97 с.

2.Глумов И.Ф., Александров В.В., Кудряшов В.Е., Костюк А.Н., Грибанов А.М. Принципы построения судовых комплексов для добычи твердых полезных ископаемых //

Сов. геол. 1990. № 12. С. 96 105.

3. Инженерная геология рудной провинции Кларион-Клиппертон в Тихом океане/Я.В. Неизвестнов, А.В.Кондратенко, С.А. Козлов и др. Тр.ВНИИОкеангеологии М-ва

природн. Ресурсов РФ и РАН. Т.197. СПб.:Наука, 2004. 281 с. 79 ил.

4.Далматов Б.И., Бронин В.Н., Заварзин Л.Г., Зеленкова Н.И. Оценка влияния гидростатического давления на уплотнение глинистых грунтов различной консистенции// Инженерная геология. 1984.№2. С. 58-60.

5.СниП 2.02.01-83* Основания зданий и сооружений .

6.Цытович Н.А. Механика грунтов. М.:Изд-во Госстроиздат , 1963.- 635 с.

536

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

УДК 625.721:625.717:624.131.5

Е.А. Исаханов (Казахская академия транспорта и коммуникаций, Алматы), С.Х. Достанова (Казахская головная

архитектурно-строительная академия, Алматы), К.Е. Токпанова (Университет «Кайнар», Алматы)

МОДЕЛИ ГРУНТОВОГО ОСНОВАНИЯ В РАСЧЕТАХ ФУНДАМЕНТНЫХ КОНСТРУКЦИЙ И ПЛИТ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ

Самой простой и наиболее распространённой моделью линейно деформируемого основания является модель Винклера. При проектировании сооружений в обычных грунтовых условиях, когда среднее давление на основание под подошвой фундаментных или дорожных плит от нагрузок не превышает расчетного значения, можно удовлетвориться результатами расчетов оснований в линейной постановке. Как показывает практика, механические свойства грунта изменяются во времени, поэтому выбор модели деформируемого основания зависит от выбранной физической и механической модели грунтового основания.

Результаты многочисленных экспериментов для большинства видов грунтов показывают нелинейный характер зависимости между напряжениями и деформациями, поэтому важно знать нелинейное поведение грунта в общей работе системы «плита-грунтовое основание».

Зная поведение грунтового основания под действием внешней нагрузки (1-ая задача), можно рассматривать обратную задачу о взаимодействии опорных конструкций, связанных с грунтовым основанием (2 задача). Эти задачи имеют большое значение при проектировании фундаментных и плитных конструкций зданий и сооружений. Используя имеющиеся опытные данные, можно с достаточной точностью описать поведение грунтового основания и выбрать соответствующую модель системы «плита-грунтовое основание». Для этого рассматривая плиту как весьма гибкую, определяем осадки основания под действием нагрузки, непосредственно приложенной к основанию.

Предлагается следующая модель грунтового основания: рассмотрим грунтовый массив (H- толщина,L,B- размеры в плане), находящийся под действием среднего давления q0, приложенного на прямоугольной площадке размером F=ab. Толщина Н принимается равной предельному значению, когда дальнейшее увеличение толщины массива не влияет на конечные результаты. Аналогично подбираются размеры L,B. Граничные условия: при z=H компоненты перемещений равны нулю, т. е. u=v=w=0.

Среднее значение нагрузки на грунтовое основание можно определить [1]:

537

Современные геотехнологии в строительстве и их научно-техническое сопровождение

где q(x,у) – интенсивность нормальной нагрузки, передаваемая на основание, a,b – размеры плиты в плане. В случае сосредоточенной силы используем разложение с применением функций Дирака.

Рассматриваются 3 модели грунтового основания:

1)линейно – деформируемое;

2)нелинейно – деформируемое (неоднородное основание);

3)ползучесть грунта при постоянной скорости интенсивности дефор-

мации.

Для расчета по 1-ой модели основания используется решение Буссинеска [1]. Для расчета по 2-ой модели основания используется уравнение состояния, которое связывает между собой интенсивности деформаций, интенсивности напряжений и среднее напряжение. Это уравнение получено экспериментально и имеет следующий вид [2]:

где в правой части функция 1 учитывает влияние интенсивности деформации и среднего напряжения на интенсивность напряжений ( i , i , ср – соот-

ветственно интенсивность напряжений, интенсивность деформаций и среднее напряжение). Функция правой части уравнения (1) получена в результате лабораторных испытаний грунта на трехосное сжатие и имеет нелинейный характер. В нелинейном решении грунт рассматривается как неоднородный упругий массив, где справедливы зависимости Генки для пространственной задачи. Используется модель малых упругопластических деформаций, т. е. задачу теории пластичности можно рассматривать как задачу теории упругости, но для неоднородного упругого тела, так как параметры упругости в каждой точке в общем случае зависят от характеристик напряженнодеформированного состояния i , i , ср .

Для 3-ей модели основания используется свойство ползучести в виде реологических уравнений состояния, которые связывают интенсивности деформаций, интенсивности напряжений, среднее напряжение и скорости деформаций между собой. Это уравнения получены экспериментально, и имеет следующий функциональный вид [2]:

где в первом уравнении (2) первый член в правой части учитывает влияние интенсивности скорости деформации, а второй член – влияние среднего напряжения. Вид функций в правой части (2) получен также экспериментально в результате лабораторных испытаний грунта на трехосное сжатие для каждого вида грунта в отдельности и имеет нелинейный характер. При расчете скорость интенсивности деформации задана i , она зависит от скоростей

538

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

деформаций и загружений грунтового основания, в общем случае она может изменяться во времени. Напряженно-деформированное состояние в каждой точке характеризуется величинами i , i , i , ср.

При численном расчете основания определяются осадки поверхности, которые в дальнейшем будут соответствовать значениям прогибов плиты в узлах налагаемой сетки w(xi, yi) i=1…..N, где N – количество узлов на наружной поверхности. Эти данные можно использовать в дальнейшем для расчета самой плиты. Они представляют собой деформированную поверхность основания и в силу полного контакта плиты с основанием можно принять их за деформированную поверхность плиты, т. е. принять прогибы плиты равными полученным осадкам поверхности грунтового основания. При расчете плиты аналитическим методом можно получить реактивное давление, соответствующее деформированной поверхности основания с использованием степенных рядов [1].

Алгоритм расчета грунтового основания с учетом уравнения состояния состоит в следующем. Согласно основной предпосылке нелинейной теории упругости, а также теории малых упругопластических деформаций при простом нагружении [3], связь интенсивности напряжений с интенсивностью деформаций для каждой точки тела при сложном напряженном состоянии принимается такой же, как связь осевого напряжения с деформацией удлинения при простом растяжении тела, т. е.

где E' – секущий модуль деформации 1-го рода. В теории пластичности при

простом нагружении, в условиях малых деформаций, это выражение дает возможность использования физических уравнений в форме зависимостей Генки [23]:

х ср 2G* x ср ; ху G* ху ; у ср 2G* у ср ; yz G* yz ; (4)z ср 2G* z ср ; хz G* xz ,

539

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Используя теорию малых упругопластических деформаций, математический аппарат представляет совокупность шести физических уравнений (4) (или (5), трех статических уравнений равновесия и шести уравнений совместности деформаций [3]. Ищется такое решение задачи, которое для каждой точки деформируемого тела удовлетворяет перечисленным выше уравнениям и, кроме того, на границе тела удовлетворяет граничным условиям. Задачу теории пластичности можно рассматривать как задачу теории упругости, но для неоднородного упругого тела, так как «параметры упругости» – E, ,G

в каждой точке тела в общем случае зависят от характеристик напряженнодеформированного состояния. Решение такой нелинейной задачи строится по методу последовательных приближений [3]. В нулевом приближении

E*(0) , *(0) ,G*(0) принимают равными E, , G и, решая линейную задачу теории упругости, находят компоненты напряжений и деформаций:

где интенсивность деформации и среднее напряжение в дальнейшем в каждом приближении вычисляются по следующим формулам:

E*(1) , *(1) ,G*(1) . Далее решается задача линейной неоднородной теории упру-

гости. Используя зависимости Генки в каждой точке, определяются компоненты напряжений и деформаций в первом приближении:

На основе уравнений состояния (1) или (2) определяются i(1) , (ср1) , Е*(2) ,

*( 2 ) , G *( 2 ) , соответствующие новому приближению. Уравнения состоя-

ния дают возможность целенаправленно варьировать напряжения и деформации во всех точках тела, сохраняя инвариантные зависимости (1) и (2).

Для определения истинного напряженно-деформированного состояния основания применяется вариационный метод в сочетании с методом упругих решений в форме переменных параметров. Последний дает возможность рассматривать основание как неоднородный массив с изменяющимися модулями. Полная энергия грунтового массива (Э), как наиболее общая характеристика системы, дает возможность быстрее получить достоверную картину поведения тела при изменяющихся параметрах упругости (в методе упругих решений сравниваются напряжения в каждом приближении, что увеличивает время поиска).

Для нахождения величины Э используем дискретизацию, т. е. грунтовый массив представляем в виде совокупности отдельных элементов. Форма

540