Сборник трудов конференции СПбГАСУ 2014 ч

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

Рис. 1. Геомеханическая модель напряженно-деформированного состояния подрабатываемого грунтового массива под подошвой ленточного фундамента с креном:

1 – грунтовое основание; 2 – ленточный фундамент; 3 – откос котлована;

bf, lf, – ширина, длина, угол наклона фундамента; P – начальная распределенная нагрузка; bc – толщина грунтовой стенки; С1,С2 … Сn – горизонтальные цилиндрические скважины; hc,d,t – глубина заложения; диаметр и шаг скважин; H0 – физическая глубина грунтового массива; PH – область зарождения начальной пластической деформации у грани фундамента; H1 – высота начальных пластических областей; P1, P2, P3 – пластические области, возникающие по линии окружности 4 диаметром Dp в грунтовом массиве при увеличении

нагрузки P; 1, 2… n – ширина кольцевых пластических областей вокруг скважин; 5 – линия разрушения грунта трещиной между рядом расположенными скважинами; ly – ширина упругого участка (целика) грунта между скважинами;

К – точка соединения пластических областей при полном разрушении грунта

Одним из основных факторов, влияющим на характер напряженнодеформированноого состояния подрабатываемого грунтового массива, является степень взаимодействия начальных пластических областей у граней фундамента с пластическими областями возникшими по контуру пробуренных цилиндрических скважин. Для исключения разрушения грунта, в процессе этого взаимодействия, глубина заложения скважин должна быть больше высоты начальных пластических областей.

Шаг и диаметр скважин определяется с учетом характера распределения величин технологических осадок по длине фундамента и рассчитывается с учетом ширины кольцевых пластически деформированных областей. При этом в области грунта между рядом расположенными скважинами не должно происходить взаимодействие кольцевых пластических областей. В значительной степени характер напряженно-деформированного состояния исследуемой системы, при взаимодействии с нагрузкой, зависит от толщины сжимаемого грунтового массива. В процессе устранения крена фундамента непрерывно происходит перераспределения полосовой нагрузки, а следовательно и непрерывное изменение напряженно-деформированного состояния подрабатываемого грунтового основания. Поэтому при разработке расчетной модели грунтового основания можно использовать принцип в основу которого

501

Современные геотехнологии в строительстве и их научно-техническое сопровождение

положено аппроксимация контура грунтового основания в виде прямоугольника (плоская задача) или параллелепипеда (пространственная задача) [1].

Если в данной расчетной модели учесть физическую толщину сжимаемого слоя, то она приблизится к реальной физической модели системы «подрабатываемое грунтовое основание – ленточный фундамент с креном». Предлагаемый вариант расчетной модели, исследуемой системы, учитывающий физическую толщину сжимаемого слоя грунта приведен на рис. 2.

Рис. 2. Расчетная схема системы «подрабатываемое грунтовое основание – ленточный фундамент с креном»:

1 – контур развития пластических областей;

2 – область грунта в котором бурятся скважины;

3 – горизонтальные цилиндрические скважины; Dp – диаметр окружности развития пластических областей bf – ширина фундамента; B – ширина грунтового массива в форме прямоугольника; H0 – физическая толщина сжимаемого слоя грун-

та; P – распределенная нагрузка

2. Расчет параметров системы «подрабатываемое грунтовое основа- ние–ленточный фундамент с креном»

В качестве основных расчетных параметров принимаются: толщина грунтового основания; толщина грунтовой стенки между ленточным фундаментом и котлованом, глубина котлована; глубина заложения, шаг, диаметр цилиндрических скважин; ширина пластических кольцевых областей, возникающих вокруг цилиндрических скважин после их бурения.

Определим физическую толщину грунтового основания, с учетом крена здания, наоснове методики, использованной при решении задачи Ренкина [2]:

где H0 – физическая толщина грунтового основания; α – угол наклона фундамента; δ – угол между нормалью к поверхности грунтового основания и направлением действия внешней полосовой нагрузки P; γ, φ – удельный вес и угол внутреннего трения грунта.

Ширина грунтовой стенки определяется по формуле:

где Dp – диаметр окружности развития пластических областей; bp – ширина пластической области в грунте в зоне отрывки котлована; bf – ширина фундамента.

502

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

Исходной величиной, для расчета диаметра горизонтальных цилиндрических скважин, является эпюра осадки ленточного фундамента, полученная по результатам геодезической съемки высотного положения здания до начала работ по устранению его сверхнормативного крена.

Технологические параметры системы «подрабатываемое грунтовое основание – ленточный фундамент с креном» взаимосвязаны между собой следующим основным соотношением:

где s – требуемая технологическая осадка; d, t – диаметр и шаг горизонтальных цилиндрических скважин.

Для исключения взаимодействия кольцевых пластических областей, сформированных вокруг пробуренных горизонтальных цилиндрических скважин, они должны быть разделены участком (целиком) грунта, работающего в упругой фазе. Ширина целика выбирается из условия, что при внешней нагрузке в нем должны возникать напряжения не больше величины расчетного сопротивления грунта.

С учетом вышесказанного шаг скважин в ряду определяется из усло-

вия:

где dvar – варьируемый диаметр скважин; c – ширина пластической кольцевой области грунта вокруг скважин; ly- ширина упругого участка грунтового целика в направлении вертикальной оси асимметрии.

Зная шаг скважин и требуемую величину технологической осадки можно определить из (3) необходимый диаметр скважин:

d 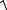S(dvar 2 c I y , (5)

и соответственно выбрать необходимый диаметр шнеков для механического бурения.

Глубину заложения горизонтальных цилиндрических скважин принимаем исходя из условия, они должны располагаться в максимально сжимаемом слое грунта, но при этом не должны пересекать начальных пластичных областей, сформированных у граней фундамента (рис. 2):

(6)

где hc – глубина заложения скважин; H1 – высота начальных пластических областей формирующиеся у грани фундамента.

Для определения текущего характера напряженно-деформируемого состояния подрабатываемого грунтового основания введем коэффициент идентификации:

V II

где: V – суммарный объем областей в грунтовом основании находящиеся в упругом состоянии; V – тоже в пластическом.

503

Современные геотехнологии в строительстве и их научно-техническое сопровождение

При выполнении условия Kі ≥ 10 грунтовое основание работает по уп- руго-деформируемой линейной модели [1] и следовательно невозможна потеря устойчивости фундамента при производстве работ по устранению его сверхнормативного крена.

Для практической реализации способа идентификации напряженнодеформированного состояния подрабатываемого грунта разработан алгоритм определения ширины пластической зоны вокруг контура цилиндрический скважин. Ранее получено аналитическое решение задачи о распределении напряжений и деформаций вокруг круглого отверстия в идеальной упруго – пластической среде с критерием пластичности Треска [3]. Это аналитическое решение является одним из наиболее точных, поэтому оно может быть использовано на участке ленточного фундамента, где нагрузка меньше величины предельного сопротивления грунта. При больших нагрузках используется численный метод определения ширины пластических зон вокруг цилиндрических скважин.

При устранении крена фундамента бурится один или несколько рядов, содержащих 1…n скважин разного диаметра. Объем пластических областей в грунтовом основании будет равен:

где d – диаметр цилиндрических скважин; c – ширина кольцевой пластической области вокруг скважин; l, n – длина и количество скважин.

Общий объем грунта, исходя из предложенной расчетной модели, ограничен физической глубиной грунтового основания, длиной скважин и дли-

где H0 – физическая глубина грунтового основания, lf – длина фундамента, l – длина скважин.

С учетом(8), (9) получим для упруго деформированного объема грунта:

3. Контроль параметров расчетной модели подрабатываемого грунтового основания

При устранении кренов зданий часто возникают расхождения в величинах фактических и прогнозируемых параметров, например, в величинах технологической осадки строительного объекта. Поэтому в проектах необходимо предусматривать дополнительные инженерные мероприятия: мониторинг в режиме реального времени, технологические приемы регулирования осадок и др. Это позволит на всех этапах выполнения работ по устранению крена здания обеспечивать равенство прогнозируемых и фактических деформаций системы «подрабатываемое грунтовое основание – ленточный фундамент с креном».

504

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

Для предложенной расчетной модели системы «подрабатываемое грунтовое основание – ленточный фундамент с креном» основными контролируемыми параметрами являются: толщина грунтовой стенки между фундаментом и котлованом; глубина котлована; глубина заложения, диаметр, шаг цилиндрических скважин; характер изменения технологических осадок и крена фундамента; коэффициент идентификации подрабатываемого грунтового основания; величина выпора грунта в зоне ленточного фундамента.

Для мониторинга вышеуказанных параметров разработана структурная схема автоматизированного их контроля и измерительно-информационная система «Мониторинг», на основе индуктивных преобразователей с периодическим сбором измерений информации о контролируемых физических величинах, с последующим их обработкой и хранением в ЭВМ [4].

Литература

1.Тер-Мартиросян З.Г. Механика грунтов. – М.: Издательство Ассоциации строительных вузов. – 2005. – 488с.

2.Харр М.Е. Основы теоретической механики грунтов. – М.: Издательство литературы по строительству. – 1971. – 320с.

3.Фадеев А.Б. Метод конечных элементов в геомеханике. М.: Надра. – 1987. –

221с.

4.Шокарев В.С. Автоматизированная система контроля и компютерного моделирования надежности и безопасности зданий / В.С. Шокарев, Н.Н. Молочкова // Проблемы

и опыт инженерной защиты урбанизированных территорий и сохранения наследия в условиях геоэкологического риска: Тр. Междунар. конф. – К.: Фенікс. – 2013 -С.85-91.

624.131.526

А.З. Тер-Мартиросян, И.Н.Лузин

(НИУ МГСУ-МИСИ, г. Москва)

ОБЗОР МЕТОДОВ ОПРЕДЕЛЕНИЯ OCR И ЕГО ВЛИЯНИЕ НА ДЕФОРМИРУЕМОСТЬ ОСНОВАНИЯ

В ряде случаев основания здания и сооружений сложены переуплотненными грунтами. Переулотненным называют грунт, ранее испытавший давление большее, чем существующее «бытовое» давление на рассматриваемой глубине. Максимальное давление, которое грунт испытал в прошлом, называют давлением предуплотнения p'c.. Целью данной работы являлось определение влияния коэффициента переуплотнения грунта на вертикальные деформации и обзор методов его определения.

Степень переуплотнения грунта оценивают коэффициентом переуплотнения OCR.

505

Современные геотехнологии в строительстве и их научно-техническое сопровождение

где OCR – коэффициент переуплотнения, д.е.; p'c – эффективное давление предуплотнения, МПа; p'0– эффективное бытовое давление, МПа. Существуют различные способы оценки давления предуплотнения, при этом сами испытания трудоемки и длительны, а графические методы интерпретации их результатов недостаточно точно характеризуют величину p'c.

Наиболее распространенным, классическим способом оценки давления предуплотнения связных грунтов является метод, разработанный Казагранде

в1936 году [2]. Способ включен в действующий Американский стандарт (ASTM) и заключается в компрессионном сжатии образца грунта при ступенчатом приложении давлений до значений, превышающих давление предуплотнения, с фиксацией величины осадки для каждой ступени давления. По полученным результатам испытаний строится компрессионная кривая

вполулогарифмическом масштабе. На графике определяется точка, соответствующая наибольшей кривизне кривой, через эту точку проводятся горизонтальная линия и касательная к кривой, затем проводится биссектриса угла между ними. Определяется точка пересечения биссектрисы с продолжением прямолинейного участка компрессионной кривой, проекция которой на ось давлений р' и дает величину давления предуплотнения рc' (рис. 1, а).

Рис. 1. Определение давления предуплотнения p'c:

а) по методу Казагранде б) по методу Беккера

Компрессионная кривая не всегда имеет ясно выраженный перегиб, что затрудняет определение величины p'c. В таком случае могут быть применены другие методы, в частности, метод Беккера [5], кратко описанный в [6]. Значение p'с находится по графику зависимости увеличения накопленной энергии деформации (напряжение, умноженное на относительную деформацию)

506

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

от приращения нагрузки в одометре. Точка, после которой энергия деформации резко возрастает, соответствует давлению предварительного уплотнения

(рис. 1б).

В ходе работы в качестве примера рассматривалась задача штампа на основании, сложенным переуплотненным глинистым грунтом. Задача решалась методом конечных элементов с применением модели Hardening soil.

Методом конечных элементов задача решалась в программном комплексе PLAXIS 2D на модели упрочняющегося грунта (Hardening soil). Расчетная схема задачи показана на рис. 2.

Рис. 2. Расчетная схема задачи в ПК PLAXIS 2D

Задача решалась для 4 значений коэффициента переуплотнения. В результате расчета были получены значения вертикальных перемещений штампа, приведенные в табл. 1.

Таблица 1

Осадка штампа при различных значениях коэффициента переуплотнения грунта основания

На рис. 3 и 4 показаны изополя вертикальных перемещений штампа при

OCR=1 и OCR=4.

507

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Рис. 3. Изополя вертикальных перемещений штампа при коэффициенте переуплотнения равном 1

Рис. 4. Изополя вертикальных перемещений штампа при коэффициенте переуплотнения равном 4

508

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

Выводы

1.При испытании грунтов ненарушенной структуры компрессионным методом необходимо проводить проверку, являются ли эти грунты переуплотненными, с последующим вычислением коэффициента переуплотнения для его учета в последующих расчетах по второй группе предельных состояний.

2.Учет коэффициента переуплотнения при расчете оснований по второй группе предельных состояний может существенно уменьшить деформируемость основания, что позволит применять более экономичные виды фундаментов.

Литература

1. Механика грунтов, основания и фундаменты. С.Б. Ухов, В.В. Семенов, В.В. Знаменский, З.Г. Тер – Мартиросян, С.Н. Чернышев, Москва, 2005.

2. Методы определения механических свойств грунтов. Состояние вопроса. Г.Г. Болдырев, Пенза, 2008.

3. PLAXIS 2D. Руководство пользователя, 2012.

УДК. 624. 131.54: 624.131.38

А.В. Пилягин (ЧПИ МГОУ г.Чебоксары)

К ВОПРОСУ ОПРЕДЕЛЕНИЯ МОДУЛЯ ОБЩЕЙ ДЕФОРМАЦИИ ГРУНТА ПО ДАННЫМ ПРЕССИОМЕТРИЧЕСКИХ ИСПЫТАНИЙ

Требования норм расчета оснований фундаментов зданий и сооружений по деформациям приводит к необходимости определения деформационной характеристики грунта – модуля общей деформации. Методика определения модуля деформации по данным прессиометрических испытаний изложена в ГОСТ 20276–99. В соответствии с данным ГОСТом модуль деформации определяется по линейному участку кривой зависимости изменения радиуса скважины в зависимости от приложенного давления по формуле

давления; r – увеличение радиуса скважины в интервале указанных давлений.

Коэффициент kz рассматривается как корректирующий коэффициент, принимающий при испытании в медленном режиме следующие значения: для песка и супеси kz =1,3; для суглинка kz=1,35 и для глин kz=1,42. При проведении испытаний по быстрому режиму значения kz принимаются по табл. 1.

509

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Таблица 1

Значение коэффициента kz

Нетрудно заметить, что коэффициент kz в первом случае заменяет собой величину (1+μ), приводимую в прежних редакциях ГОСТов соответственно для песков и супесей μ=0,3; суглинков μ=0,35 и глин μ=0,42. Анализ таблицы 1 показывает, что с ростом показателя текучести увеличивается значение kz, а следовательно и модуль общей деформации, что не соответствует действительности.

Кроме того значение kz снижается с увеличением глубины скважины, что приводит к снижению модуля общей деформации. Фактически модуль общей деформации грунтов с увеличением глубины должен возрастать. Как известно, формула определения модуля общей деформации грунта по данным прессиометрических испытаний базируется на осесимметричной задаче Ламе о напряжениях и перемещениях толстостенной бесконечно длинной трубы под действием внутреннего и внешнего давлений.

Полное решение задачи Ламе можно найти в курсах теории упругости. Нас интересуют перемещения трубы под действием внутреннего давления Рв и наружного давления Рн от собственного веса грунта на глубине проведения испытаний.

Обратимся к выводу формулы Ламе (рис.1a), для чего рассмотрим равновесие элементарной трапеции А1В1С1Д1 сечения цилиндра с центральным углом dβ. На боковых гранях А1В1 и С1Д1 будут действовать окружные напряжения σθ; а на внутренней поверхности элемента А1Д1 радиальные σr. На внешней границе В1С1 радиальные напряжения будут равны σr+ dσr. В виду симметрии кольца и нагрузок выделенный элемент не будет перекашиваться, следовательно, на его гранях будут отсутствовать касательные напряжения. Поэтому напряжения σr и σθ будут главными, а величина σθ не будет зависеть от полярного угла β.

Уравнение равновесия для элемента А1В1С1Д1 в виде суммы всех сил на нормаль к цилиндрической поверхности выглядит следующим образом

510