Сборник трудов конференции СПбГАСУ 2014 ч

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

Разрезные кольца ячейки изготовлены из полиэтилена низкой плотности (LDPE). Для минимизации трения мерзлого грунта внутреннюю поверх-

391

Современные геотехнологии в строительстве и их научно-техническое сопровождение

ность ячейки покрыли антифрикционной смазкой. Для размещения датчиков температуры внутри образца в ячейке предусмотрены отверстия на контакте двух смежных разрезных колец. При подготовке образца к испытанию установлено 4 датчика температуры внутри образца и 10 датчиков – в холодильной и морозильной камерах. Все датчики температуры управляются специально запрограммированным микроконтроллером персонального компьютера.

ЛАБОРАТОРНЫЕ ЭКСПЕРИМЕНТЫ

Лабораторные эксперименты проведены с 14 образцами супеси, содержащими не более 5 % гравия. Каждый образец имел диаметр 100 мм и высоту – 150 мм. Физические характеристики образцов перед началом испытаний представлены в табл. 1. Плотность и влажность образцов супеси соответствовали образцам ненарушенной структуры в природном залегании.

Таблица 1

Физико-механические характеристики грунта

392

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

Испытания выполнены в 2 этапа: первый этап – охлаждение образца до температуры +1…+2 oC в холодильной камера в условиях свободного водонасыщения образца снизу; второй этап – промораживание грунта с заданной скоростью при постоянном давлении, равном 12,5 кПа. Скорость промерзания установлена 10 мм/ сут, что соответствует климатическим условиям г. Архангельска.

Зависимость температуры грунта по высоте образца представлена на рис. 3. Скорость промерзания в ходе эксперимента составила 8 ... 10 мм/ сут.

Ксожалению, нам не удалось обеспечить заданную скорость промерзания

впервые 24 часа.

Рис. 4. Зависимость деформаций морозного пучения от времени

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

Численное моделирование лабораторных экспериментов выполнено в осесимметричной постановке в программно-вычислительном комплексе GeoStudio 2012. Для моделирования поведения грунта в процессе промерза-

ния использована модель Coupled Convective Thermal (CCTM), основными параметрами которой являются:

1.Зависимость коэффициента теплопроводности от влажности;

2.Зависимость удельной теплоемкости от влажности;

3.Зависимость содержания незамершей воды от температуры.

Вчисленной модели грунта зависимость коэффициента теплопроводности от влажности грунта определено по выражению O. Johansen [12]:

где sat и dry = коэффициент теплопроводности полностью водонасыщегого и абсолютного сухого грунта соответсвенно; Ke = коэффициент, принимаемый равным: для талых песков со степенью влажности Sr>0.05

393

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Коэффициент теплопроводности полностью водонасыщенного талого грунта вычисляется по формуле (4), а мерзлого по формуле (5):

где s = коэффициент теплопроводности твердых частиц; i = коэффициент теплопроводности льда; w = коэффициент теплопроводности воды; n = пористость грунта.

Коэффициент теплопроводности dry определяют по формуле:

где d = плотность сухого грунта (кг/м3).

Зависимость коэффициента теплопроводности от влажности при раз-

личном значении s показано на рис. 5. Кривая 1 соответствует

s=3,0 Вт/(мoC), кривые 2 и 3 – 4,5 and 6,0 Вт/(мoC).

В ходе эксперимента коэффициент теплопроводности грунта определили зондовым методом при помощи прибора МИТ-1. Измерения теплопроводности выполнили при влажности грунта 0; 0,10; 0,15; 0,20; 0,25. Результаты измерений представлены на рис. 5 (кривая 0).

Функция удельной теплоемкости от влажности определена при удельной теплоемкости твердых частиц супеси равной 0,71 Дж/(гoC). При этом влажность в численной модели задана в виде зависимости от потенциала всасывания (matrix suction). В связи со сложностью выбора этой зависимости приняли 4 различные функции соответствующие четырем разновидностям глинистых грунтов: loamy sand, sandy loam, sandy clay и silty clay.

Функции изменения содержания незамершей воды от температуры приняты для указанных грунтов с учетом рекомендаций GeoStudio 2012.

Свойства материалов численной модели автоматизированной установки представлены в табл. 2.

Рис. 5. Зависимость коэффициента теплопроводности от влажности (n=0.39): * – экспериментальная кривая; **- вычисленная по формуле (1).

394

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

Для численного моделирования процессов промерзания выполнили совместный температурный и фильтрационный расчеты в условиях нестационарного теплового потока. Общая продолжительность численного эксперимента составила 10 дней, что соответствовало продолжительности лабораторных испытаний. Первоначально, для численной модели приняли зависимость коэффициента теплопроводности от влажности, полученную экспериментальным путем (кривая «0», рис. 5). Результаты моделирования после завершения эксперимента представлены на рис. 6.

Для оценки применимости различных зависимостей коэффициента теплопроводности от влажности (рис. 5) и моделей грунта на скорость промерзания, поставлены численные эксперименты. Для оценки расхождения расчетных температур от наблюдаемых на глубине z вычислили среднее отклонение (Sx) по формуле:

1

где Ti = расчетная температура на глубине z, oC; Tobs= наблюдаемая температура на глубине z, oC; n = количество точек наблюдений.

Результаты численных экспериментов представлены в табл. 3.

Таблица 3

Среднее отклонение температуры по глубине образца

Примечание. * – см. рис. 7.

395

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Наиболее близкие результаты к наблюдаемым температурам показали численные модели, представленные грунтами loamy sand (вариант № 1)

и sandy loam (вариант № 2).

Выводы

Результаты численного моделирования и экспериментальных исследований процессов промерзания грунтов показали:

1. Mодель Coupled Convective Thermal с достаточной степенью точ-

ности моделирует процессы промерзания в полностью или неполностью водонасыщенных, мерзлых и талых грунтах (рис. 9). При варьировании коэф-

фициента теплопроводности 30 % (рис. 7) среднее отклонение расчетных температур от наблюдаемых не превышает 0,26…0,31oC, что соответствует отклонению при определении глубины промерзания не более чем на

1,0…1,25 см.

2.Скорость промерзания может быть определена на основе численного моделирования результатов лабораторных исследований грунтов.

3.Модель Coupled Convective Thermal дает возможность планировать режим испытаний грунтов в лаборатории при заданной скорости их промерзания.

4.Деформации морозного пучения в полевых условиях могут быть спрогнозированы на основе численных моделей грунтов, адаптированных по результатам лабораторных экспериментов.

396

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

Литература

1.ГОСТ 28622-2012. Грунты. Метод лабораторного определения степени пучинистости. М.: МНТКС, 2012. 12 с.

2.Ганелес Л.Б., Оржеховский Ю.Р., Юрганов М.М. Лабораторный метод определения морозной пучинистости грунтов // Инженерно-геокриологическое обеспечение строительства сооружений: сборник научных трудов. Новосибирск: Наука, 1989. С. 41-46.

3.Ершов Э.Д. Общая геокриология. М.: Недра, 1990. 559 с.

4.Ершов Э.Д. Физикохимия и механика мерзлых пород. М.: Изд-во МГУ, 1986.

336 с.

5.Невзоров А.Л. Фундаменты на сезоннопромерзающих грунтах. М.: АСВ, 2000.

152 с.

6.Невзоров А.Л., Коршунов А.А., Чуркин С.В. Прибор для определения деформаций и сил морозного пучения грунта. Геотехника: Теория и практика // Межвузовский тематический сборник трудов. СПб.: Изд-во СПбГАСУ, 2013. С. 183–185.

7.Оржеховский Ю.Р., Ганелес Л.Б. Прибор и методика определения морозоопасности грунтов // Материалы 3-го Научно-технического семинара «Инженерногеологическое изучение и оценка мерзлых, промерзающих и протаивающих грунтов»

(ИГК-92). СПб.: Изд-во ВНИИГ, 1993. С. 71-74.

8.Шевченко Л.В., Лапшин В.Я. Морозное пучение грунта при различных криогенных текстурах с учетом его усадки // Мерзлотные исследования. М.: Изд-во МГУ, 1977. Вып. 16. С. 188-194.

9.Andersland, Orlando B. 2004. Frozen ground engineering. New Jersey: John Wiley&

Sons.

10.Konrad J.M. Frost heave mechanics: Ph.D.Thesis. Edmonton, Alberta, Canada, 1980.

472 p.

11.Konrad J.M. Procedure for determining the segregation potential of freezing soils. Geotechnical Testing Journal. V. 10. № 2. 1987. P. 51-58.

12.Thermal Modeling with TEMP/W. 2012. An Engineering Methodology. http://www.geo-slope.com.

УДК 624.131

П.А. Горбачев (ФГБОУ ВПО "МГСУ", г. Москва)

КОНТАКТНОЕ ВЗАИМОДЕЙСТВИЕ ОДИНОЧНОЙ СВАИ С ПУЧИНИСТЫМ ГРУНТОМ

Сваи, погруженные в сезоннопромерзающие пучинистые грунты, испытывают воздействие выдергивающих касательных сил по боковой поверхности (рис. 1). В случае небольшой загрузки на оголовок и недостаточной заделки сваи в талые слои происходит её выдергивание.

Анализ экспериментальных исследований [2, 7, 11] показывает, что взаимодействие сваи с пучинистым грунтом носит сложный пространствен- но-временной характер. Выдергивающее усилие Nвыд – один из ключевых параметров, оцениваемых в экспериментах, зависит от характеристик тепломассопереноса промерзающего грунта, его механических характеристик и параметров контакта на границе свая-грунт.

397

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Рис. 1. Расчетная схема задачи:

Еp, νp, Еf, νf, Еth, νth – механические характеристики сваи,

мерзлого и талого грунта соответственно; a, lp – радиус и длина сваи; b – радиус влияния сваи; h – высота модели; sb – вертикальное перемещение дневной поверхности свободно пучащегося грунта; df – сезонная глубина промерзания грун-

та; εfh,x, εfh,y – горизонтальная и вертикальная деформации

морозного пучения грунта соответственно; τfh – касательное напряжение морозного пучения; τуд – удерживающее расчетное сопротивление грунта сдвигу

Очевидно, что исследование напряженно-деформированного состояния (НДС) в пучинистом грунте должно проводиться совместно с решением задачи о тепломассопереносе [9,12]. Однако из-за больших математических трудностей силовое взаимодействие сваи с пучинистым грунтом, как правило, рассматривается отдельно от задачи тепломассопереноса при использовании различных упрощений и допущений [8,10].

Винженерных целях для оценки касательных сил морозного пучения, действующих по боковой поверхности сваи, в ряде случаев оправдано использование метода конечных элементов (МКЭ).

Внастоящей работе рассмотрены теоретические основы численного моделирования взаимодействия сваи с пучинистым грунтом. В используемой конечно-элементной модели приняты следующие предположения и допущения:

1.Грунт считается линейно деформируемой средой;

2.Морозное пучение грунта происходит мгновенно;

3.Свая полностью неподвижна;

4.На контакте свая-грунт принимается условие Кулоновского трения.

398

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

Известно, что мерзлый грунт обладает ярко выраженными реологическими свойствами [1]. Однако, согласно исследованиям [6], их учет при моделировании взаимодействия сваи с пучинистым грунтом не дает существенного изменения выдергивающего усилия по сравнению с линейной моделью грунта, принятой в настоящей работе.

Согласно используемому квазистатическому подходу процесс пучения представлен в виде набора стационарных состояний, для которых производится оценка силового взаимодействия сваи с грунтом. Положение фронта промерзания, отделяющего слой пучинистого грунта от талого, находится из проведенного отдельно расчета тепломассопереноса. Будем считать, что вертикальная εfh,y и горизонтальная εfh,x деформации морозного пучения в слое грунта развиваются мгновенно. Их величины предпочтительно определять из экспериментов по промораживанию образцов грунта [2, 4]. При отсутствии результатов экспериментов величины εfh,y и εfh,x могут быть найдены из решения задачи тепломассопереноса в пучинистом грунте [5].

Жесткость вышестоящих конструкций способна существенно влиять на характер взаимодействия сваи с пучинистым грунтом. В данной работе для упрощения расчетов свая считается абсолютно неподвижной.

Моделирование контактного взаимодействия сваи с пучинистым грунтом во многом определяет правильность решения рассматриваемой задачи. Многими авторами параметры контактного взаимодействия задаются путем аппроксимации данных экспериментов [2, 8]. В настоящей работе при определении касательных напряжений по боковой поверхности сваи использованы экспериментальные результаты, полученные Г.Н. Полянкиным [6].

Описание численного моделирования процесса тепломассопереноса

врамках данной работы не приводится в целях экономии места. Оценка взаимодействия одиночной сваи с пучинистым грунтом проводилась при использовании ПК Plaxis для различных фиксированных моментов времени

втечениепроцесса промерзания при исходных данных, приведенных в табл. 1. Рассмотрим полученный в результате конечно-элементного моделиро-

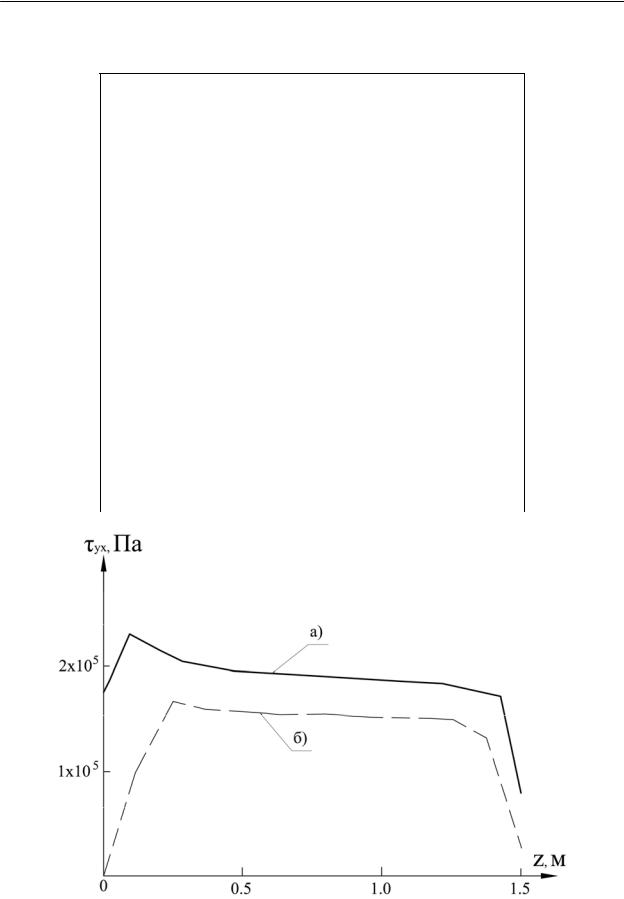
вания график изменения контактного касательного напряжения по длине сваи для момента достижения фронтом промерзания сезонной глубины.

Распределение касательного напряжения τyx по длине сваи практически равномерное (рис.2, а). Моделирование аналогичной задачи c использованием ПК ANSYS дало существенное расхождение τyx в точках, близко расположенных к поверхности, что связано с близостью сингулярной точки. На достаточном удалении от дневной поверхности величины τyx сопоставимы (расхождение составило ~25%), а характер их изменения по координате z аналогичен результатам, полученным с применением PLAXIS (см. рис.2 б). При сравнении изополей параметров НДС выявлены расхождения величин напряжений в точках контакта, что можно объяснить особенностями конечно элементной формулировки контактной задачи в каждой из программ, при этом характер распределения напряжений в обоих случаях одинаковый.

399

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Таблица 1

Исходные данные

Механические параметры модели [3]

Рис. 2. Графики распределения контактного касательного напряжения τyx (Па) по длине сваи z (м): а) PLAXIS; б) ANSYS

400