
Сборник трудов конференции СПбГАСУ 2014 ч
.1.pdf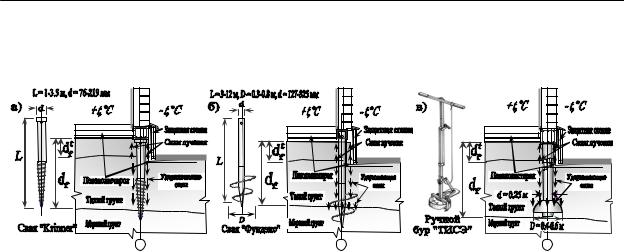
Раздел 3. Аналитические и численные методы исследований оснований и фундаментов
мерзания и соответственно – серьезной опасности выпучивания фундаментов на коротких свах.
Рис. 2. Теплоизолированные фундаменты с использованием коротких стальных свай «Krinner» (а), «Фундэкс» (б) и коротких бетонных свай «ТИСЭ» (в)
Но в России с ее холодными территориями, если оставить недостроенный дом на зиму в незащищенном от промерзания виде, опасность выпучивания свай будет вполне реальной. Стальные сваи, как и бетонные, более теплопроводны, чем грунт; они могут служить центрами льдообразования и провоцировать начало неравномерного пучения.
Например, известно, что одна из свай в составе фундамента со сваями «Krinner» за зиму 2010–2011 гг. получила подъём до 12–14 см, а расположенные рядом 2–3 сваи по обе стороны от нее остались неподвижными. Поэтому такие сваи требуют защиты от промерзания, варианты которых [4, 5] показаны на рис. 2.
Фундаменты на коротких сваях можно делать как летом, так и зимой. При выполнении зимних работ нужно проверить, как соотносятся силы пучения уже промерзшего грунта и удерживающие силы нижнего, еще незамерзшего грунта. Далее будет показано, что лопастные сваи «Фундэкс» и «Металлист» с уширениями внизу свай в виде лопастей более устойчивы от действия сил морозного пучения.
Оценка условий выпучивания коротких свай
Выпучивание свай становится реальным, когда глубина промерзания на текущий момент времени dtf превысит критическую глубину dtf,сr, либо если нагрузка на сваю N окажется меньше критической Ncr.
Условие устойчивости ненагруженных свай имеет вид [6]
Fаf – N ≤ Frf γc / γn, (1)
где Fаf – суммарная сила выпучивания (активная); Frf – сила сопротивление грунта (реактивная), препятствующая выпучиванию; N – вертикальная нагрузка, учитываемая с коэффициентом надежности f = 0.9; γc = 1.0; γn = 1.1 – коэффициенты соответственно условий работы и надежности.
Для короткой сваи, не нагруженной внешней нагрузкой, сила выпучивания зависит от площади смерзания сваи с грунтом: Fаf = τfh Af h, где τfh – удельная сила пучения грунтов, тс/м2; Afh = π dств. dtf – площадь смерзания
381

Современные геотехнологии в строительстве и их научно-техническое сопровождение
сваи с грунтом, м2; dств.– диаметр ствола сваи в пределах глубины промерзания, м.
Реактивная сила сопротивление грунта Frf складывается:
– для свай «Krinner» – из сил сопротивления грунта на боковой поверх-
ности сваи ниже границы промерзания F'rf = [π d'ств.(L– dtf) fj]/ γn, где d'ств. – диаметр ствола сваи ниже глубины промерзания, м; L – длина свай, м; fj –
удельное сопротивление грунта на боковой поверхности, тс/м2;
– для свай «Фундэкс» и «Металлист» с лопастями внизу – из сил сопротивления грунта на боковой поверхности F'rf и сил сопротивления грунта
сжатию F''rf по площади уширения нетто Frf = F'rf = γc Aо R / γn, где Aо = π (D2–
– dств.2) / 4; R – расчетное сопротивление грунта над уширением, принимаемое как для набивных свай [7]; D – диаметр уширенной пяты или лопасти, м.
1. Критическая глубина для свай «Krinner» Из условия устойчивости сваи
π dств. dtf τfh – N f ≤ γc π d'ств.(L – dtf ) fj / γn |
(2) |
следует выражение для критической глубины промерзания dtf,сr |
|
dtf,сr ≤ (N f + γc / γn π d'ств. L fj) / [π (dств. τfh + γc / γn d'ств. fj)]. |
(3) |
2. Критическая глубина dtf,сr для свай с уширенной пятой или лопастью |
|
внизу |
|
dtf,сr ≤ [N f + γc / γn (π dств. L fj + Ао R)] / [π dств (τfh + γc / γn fj)]. |
(4) |
Также очевидно, что если нагрузка на сваи уже частично передана, можно найти такую (критическую) нагрузку Ncr (включая вес сваи Nсв), при которой свая будет устойчивой при достижении или превышении нормативной глубиной промерзания длины сваи, т. е. при dfn ≥ L.
Соответствующая формула для Ncr следует из преобразования формул
(3 и 4):
для свай «Krinner»
|
Ncr ≥ [π dfh (dств ср. τfh + γc / γn d'ств fj) – γc / γn π d'ств L fj] / f . |
(5) |
для свай «Фундэкс» и «ТИСЭ» |
|
|
|
Ncr ≥ [(π dств dfh (τfh + γc / γn fj) – γc / γn (π dств L fj + Ао R)] / f. |
(6) |
Примеры расчета критической глубины dtf,сr и критической нагрузки Ncr
Приведенные в табл. 1 расчеты критической глубины dtf,сr и критической нагрузки Ncr для коротких свай выполнены для условий г. Екатеринбурга, где нормативная глубина промерзания dfh = 1.72 м, среднего по свойствам грунта – полутвердого суглинка с показателем текучести IL = 0.20 и относительной деформацией морозного пучения εfh = 0.035. В расчетах принято: удельная сила пучения грунтов τfh = 7.0 тс/м2 [6], сопротивление на боковой поверхности свай fj = 2.5 тс/м2, сопротивление под концами свай R = 6.5 тс/м2 [7]. Во внешние нагрузки включается вес сваи с коэффициентом надежности по нагрузке f = 0.9.
382

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов
Таблица 1
Результаты расчетов критической глубины dtf,сr и критической нагрузки Ncr на сваи
Параметры |
Свая «Krinner» |
Свая «Фундэкс» |
Свая «ТИСЭ»: |
Вес сваи Nсв, тс |
0.05 |
0.1 |
0.15 |
Длина сваи L, м |
2.0 |
2.0 |
1.6 |
Диаметр ствола dств., м |
0.1 |
0.168 |
0.25 |
Диаметр ствола d'ств , м |
0.075 |
– |
– |
Диаметр лопасти D, м |
– |
0.50 |
0.50 |
Критическая глубина dtf,сr, м |
0.41 |
0.72 |
0.53 |
Критическая нагрузка Ncr, тс |
3.32 |
5.54 |
8.81 |
Из приведенных расчетов следует:
выпучивание коротких ненагруженных свай без их утепления может
произойти примерно к концу ноября – середине декабря, когда глубина промерзания достигнет значений dtf,сr;
при достижении нормативной глубины промерзания dfn = 1.72 м возможенподъемсвай за счет пучениягрунта; например, свай«Krinner» подъем может
достигнуть S = – εfh (dfn – dtf,cr ) = –0.035 (1.72 – 0.41) = –0.046 м= –4.6 см;
в более пучинистых грунта, где удельная сила пучения достигает τfh = 11.0 тс/м2, а также при наличии ростверка (когда к выдергивающим факторам добавляются силы нормального пучения под его подошвой), критическая глубина dtf,сr меньше; поэтому обязательное требование – утепление подошвы ростверков на участках между отдельными сваями;
если длина сваи превысит нормативную глубину dfn (например, для сваи «Фундэкс» длиной L = 2.0 > dfn = 1.72 м), устойчивость свай возрастет, но к этому моменту свая уже может получить деформацию подъема;
сваи «ТИСЭ» более уязвимы для пучения, поскольку имеют доста-
точно развитую поверхность смерзания (диаметр сваи вверху dств.= 0.25 м против dств.= 0.168 м у свай «Фундэкс»); опасность выпучивания также обусловлена меньшей длиной сваи (L = 1.6 м) против глубины промерзания, по-
скольку при достижении глубины промерзания dfh = 1.72 м под ее уширением могут возникнуть силы нормального пучения в объеме грунта, проморожен-
ного под концом Fn = Ао σn (dfh – L) = 0.147 · 50 (1.72 – 1.60) = 0.88 тс, где
σn = 0.05 кгс/см3 = 50 тс/м3 – значение нормального давления пучения [8]. Из этих же расчетов следует, что приложенная к сваям вертикальная
нагрузка Ncr уменьшает возможность выпучивания, однако эта нагрузка достаточно велика, особенно для свай «ТИСЭ» с развитой боковой поверхностью в зоне промерзания.
Заключение
В заключение напоминается, что пучение носит вероятностный характер. Выпучивание может возникнуть в каком-то одном месте, одновременно за-
383

Современные геотехнологии в строительстве и их научно-техническое сопровождение
щищая близкие сваи от выпучивания, т. е. носит волнообразный характер и сопровождается образованием бугров пучения (именно здесь происходит выпучивание коротких свай). Поэтому приведенными выше расчетами прогнозируется только возможность образования выпучивания либо его отсутствие, но без указания конкретного места, где пучение может реально возникнуть.
Литература
1.Лушников В.В. Теплоизолированный фундамент индивидуального дома. –
СПб: 2013. – 95 с.
2.Патент на полезную модель «Теплоизолированный фундамент» / В.В. Лушников и И.С. Горьков. – Уведомление ФИПС от 28.11.2011.
3.Яковлев Р.Н. Универсальный фундамент. Технология ТИСЭ. – М.: Изд-во
«Аделант», 2006. – 240 с.
4.Патент RU № 2430214. Способ сооружения свайных фундаментов в промерзающих пучинистых грунтах / В.В. Лушников. – Опубл. 20.05.2011. Бюл. № 14.
5.Патент RU № 116160. Свайный фундамент из коротких свай в промерзающих пучинистых грунтах / В.В. Лушников, А.В. Фомичев и И.С. Горьков. – Опубл. 20.05.2012. Бюл. № 14.
6.СП 22.13330.2011. Основания зданий и сооружений (актуализированная редак-
ция СНИП 2.02.01-83*). – М.: 2011.
7. |
СП 24.13330.2011 Свайные фундаменты (актуализированная редакция |
СНиП 2.02.03-85). – М.: 2011. |
|
8. |
Руководство по проектированию оснований и фундаментов на пучинистых |
грунтах / НИИОСП им. Н.М. Герсеванова. – М.: Стройиздат, 1979. – 37 с.
УДК 624.131+539.215
Ш.А. Алтынбеков (ЮКГПИ, г.Шымкент, Казахстан)
ОБ ОДНОЙ КРАЕВОЙ ЗАДАЧЕ ТЕОРИИ ФИЛЬТРАЦИОННОЙ КОНСОЛИДАЦИИ СОЛЕНЫХ ГРУНТОВ
Введение
Встроительстве промышленных, гражданских и гидротехнических сооружений, как известно, возникают задачи о прочности и увеличения срока эксплуатации этих сооружений. Решение этих задач во многом зависит от правильной оценки и определений осадки грунтовых оснований во времени, обусловленной консолидацией грунтов.
Внастоящее время теория фильтрационной консолидации многокомпонентных грунтов, основанная на модели К. Терцаги-В.А.Флорина, признана достаточно разработанной. Однако, несмотря на это, в этой области исследования достаточно много нерешенных вопросов. Один из них, процесс осадки соленых грунтов недостаточно изучен. А ведь некоторые области
384
Раздел 3. Аналитические и численные методы исследований оснований и фундаментов
Молдавии, России, Украины, Средней Азии и Казахстана состоят из соленых грунтов. Этот вопрос в свое время поднял академик НАН РК Ш.М.Айталиев.
В данной работе приводится решение поставленной задачи. Получено основное уравнение и сформулирована математическая постановка начальнокраевой задачи консолидации соленых грунтов, исследованы свойства и решение этой задачи.
1. Постановка задачи.
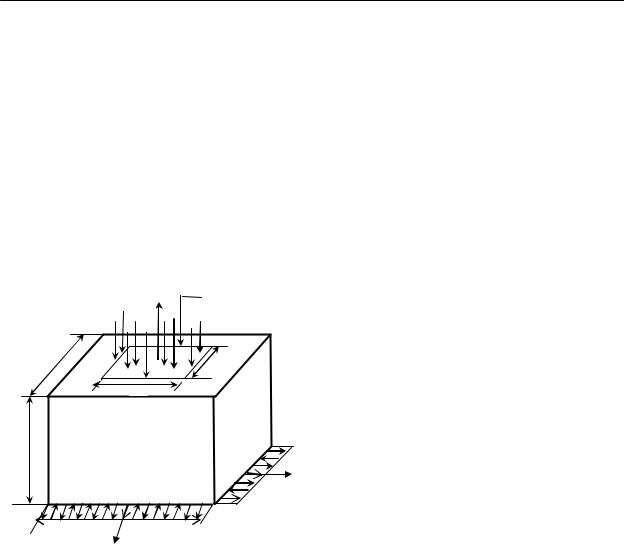
Рассмотрим процесс уплотнения соленых грунтов в виде параллелепипеда под действием распределенной нагрузки q, приложенной к части наружной площади (рис. 1).
|
|
|
|
Для изучения этого процесса |
|||
|
|
q |
|
допустим: |
|
|
|
|
|
|
Соленый грунт состоит из |
||||
|
|
|
|
||||
|
|
x3 |
|
твердой, жидкой и газообразной |
|||
2ℓ1 |
A2 |
A3 |
|
фаз. |
|
|
|
|
|
Движение |
жидкости, |
за- |
|||
|
2a |
|
|||||
A1 |
|
|
|||||
2b |
A4 |
|
полняющей поры грунта, доста- |
||||
|
|
||||||
|
|
|
|
точно |
хорошо |
согласуется |
|
|
|
|
|
с обобщенным законом Дарси- |
|||
h |
|
|
|
Герсеванова. |
|
|
|
|
|
|
x2 |
Растворимость газа подчи- |
|||
|
|
|
нена закону Генри. |
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
Растворенная соль (солевой |
||
2ℓ2 |
x1 |
|
|
раствор) движется с водой, а пена |
|||
|
|
|
|
газа и нерастворенная соль дви- |
|||
|
|
Рис. 1 |
|
жется с твердой фазой. |
|
||
|
|
|
НДС скелета соленого грунта |
||||
|
|
|
|
описывается уравнением вида [1] |
|||
(t) 1 |
1 |
|
|
|
|
1 (n 1) 2e 3x3 |
|
|
|||
|
|
|
t |
|
|
|
5e 6x3 )a0 (t (x), (t)) (t) |
|
, (1) |
||
( 4 |
( )K (t (x), (x), x, ( ))d |
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
K (t (x), (x), x, ( )) ( 4 5e |
x |
|
a0 |
( (x), ( )) |
|
|
||
6 3 ) |
|
|
|
|||||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
( 12 13e 14x3 ) |
f ( (x), ( )) |
C(t (x), (x), ( )) . |
(2) |
|||||
|
||||||||
Здесь a0 (t, x, (x), (t)) , |
( ) |
|
|
|
|
|
|
|
f ( (x), ( )) |
|
и |
C(t (x), (x), ( )) – |
|||||
функции, характеризующие физико-механические свойства грунта. Функция (x) , характеризующая закон изменения возраста материала
в зависимости от координат, аппроксимирована в виде [2]
385

Современные геотехнологии в строительстве и их научно-техническое сопровождение
(x) (x |
n |
) (x |
n |
|
( )) (0) |
|
|
|
|
39 |
|
|
39 ; |
(3) |
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
h |
max |
|
|
|
40 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max min |
40 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
xn ( ) h |
|
max |
|
0 |
при max , |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
при |
|
min , |
|
|
|
|
|
|||||||||||||
|
|
max min |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
при |
max , |
|
|
|
|
|
|||||||||||||
(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
n |
) |
|
39 |
|
|
|
39 |
при |
min , |
39 1, |
0 40 h; |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
h 40 |
|
|
40 |
|
|
|
|
|
|
|
39 |
|
39 ; |
|
|
||||||||||||||||
(x) (x |
n |
) (x |
n |
( )) |
(0) |
|
|
|
|
|
|
|
(4) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
e max e |
|
|
40 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e max |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e min |
|
|
|
|
|
||||||
xn ( ) h |
|
e max |
e |
|
|
|
0 |
при |
|
|
max , |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h. |
|
||||||
e max e min |
|
при |
|
|
min , 40 |
1, |
0 43 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
h |
|
|
|
||||||||||||||||||||||||
Соленые грунты по водопроницаемости являются анизотропной средой. При этом коэффициент фильтрации может быть аппроксимирован функцией вида [3]
|
(t) k |
nk |
|
|
|
|
|
|
, nk |
1, |
(5) |
||
|
||||||
K ( (t)) K0 |
0 k |
|
||||
|
|
|
|
|
где K0 , 0 , k и nk – опытные данные.
Процесс уплотнения соленых грунтов подчинен модели К. Терцаги – В.А.Флорина [4,5].
Во всех поверхностях консолидируемого слоя грунта (рис. 1) происходит свободный водообмен с окружающей средой.
Тогда, присоединяя к (1) основное уравнение консолидации соленых грунтов [6]
|
v ( , H )(3 * 1 ) |
H |
|
t |
|
t |
|
|
|
|
* |
|
|
|
H |
|
|
|
|
|
|
|
||
(3 |
1 ) |
|
|
|
|
|
|
|
||||||||
|
x |
x |
|
x |
|
|||||||||||
|
K1 |
|
|
2 |
K2 |
|||||||||||
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
||
и гипотезы В.А.Флорина [5] |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
||
|
|
|
|
|
|
|
|
H |
|
H , |
||||||
|
|
|
|
(t) n |
|
|
|
|||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нетрудно задать краевую задачу в виде |
|
|
|
|
|
|
|
|
||||||||
H C |
vn |
(x,t (x), * , H * , H )L(H ) |
C |
|
(x,t |
|||||||||||
t |
|
|
|
|
|
|
|
|
|
|
|
|
1n |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
H |
|
|
|
|
|
|
||||
|
|
|
|||||
|
|
|
K3 |
|
|
||
x2 |
|
x3 |
x3 |
||||
(x), * , H * , H )
386

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x), (x), * , H * , H )d |
|
|
|
||||||||||||
f ( (x), * , H * , H ) K1 (x,t |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (t (x), * , H * , H ) K2 (x,t |
(x),t (x), * , H * , |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
H ) |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
, H |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6) |
||||||||
C2n (x,t (x), |
|
|
|
, H ) L(H ) ; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
H |
H (x, 1 ) H0 (x) , x D ; |
|
|
|
|
|
|
|
|
|
|
|
|
(7) |
||||||||||||||||||||||
( ) |
|
|
|
|
( 1) |
H |
|
|
|
|
|
0, (x,t) D [ ,T ], |
|
|
|
|
|
|
|
|
|
(8) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
S |
n |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
* |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
* |
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, H |
, |
H ) |
|
|||||
K1 (x,t (x), (x), |
, H |
, H ) |
|
|
|
|
C(x,t (x), (x), |
|
|
, (9) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
* |
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
, H |
* |
, H) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C(x,t (x), (x), |
|
|
|
|
|
|
|||||||||||||||||
K2 (x,t (x),t (x), , H |
|
, H) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
, (10) |
||||||||||||
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
||
L(H ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
S |
(x,t (x), |
, H |
|
, H ) |
|
|
|
|
|
|
|
|
|
(11) |
||||||||||||||||||
|
|
|
|
K |
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
S 1 xS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xS |
|
|
|
|
|
|
|
|
||||||||
Вид функций C |
vn |
(x,t (x), * , H * , H ) , C |
|
(x,t (x), * , H * , H ) , |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (t (x), * , H * , H ), |
|
C2n (x,t (x), * , H * , H ) , C(x,t (x), (x), * , H * , H ) , |
|||||||||||||||||||||||||||||||||||
K S (x,t (x), *, H * , H ) в (6), (9), (10) и (11) обусловлен зависимостями (1),
(2), (4) и коэффициента объемной сжимаемости [6] |
|
|||||
v ( , H ) |
2 * 1 |
|
|
1 |
. |
|
3 * |
1 |
(H x3 H0 ) |
||||
|
|
|
||||
Здесь *0 и H0* обозначают сумму главных напряжений в скелете грунта
и напоров поровой жидкости, соответствующие граничным значениям непосредственно после приложения нагрузки в предположении мгновенной ста-
билизации; – растворимость газа; * – коэффициент водонасыщенности уплотняемой среды ( * 1, 1 1, 0 ); 1 – коэффициент растворимости соли (0 1 1); – удельный вес жидкой солевой смеси; – коэффициент по-
ристости, которая определена уравнением (1); |
2 j |
|
|
2 j |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1i |
x1 |
|
B1i sin |
|
1i |
|
|
|
x2 |
B2 j sin |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
H0 (x) Dij cos |
2 |
|
2 1 |
x1 |
cos |
2 2 |
2 2 |
x2 |
|||||||||
i 1 j 1 |
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
(ch 3ij x3 |
Fij sh 3ij x3 ) ; |
|
|
|
|
|
(12) |
|||||||||
решение следующей задачи [7]:
L(H ) 0 ,
387

Современные геотехнологии в строительстве и их научно-техническое сопровождение
|
|
|
( ) H |
|
( 1) |
H |
|
|
|
0 , |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
n |
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|||||||||
(3) H |
(4) H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
q / , | x | a , |
| x |
2 |
|
| b , |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
3 n |
|
3 |
|
|
|
|
x3 |
h |
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(3) H (4) H |
|
|
|
|
|
0 |
, |
1 |
x |
|
a , a x |
1 |
, |
|||||||||||
|
|
|
|
|
|
|||||||||||||||||||
3 n |
3 |
|
|
x3 |
h |
|
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 x2 b1 , b x2 2 . |
|
|
|
|
|
|
||||||||||||||||
Коэффициенты водоотдачи |
|
|
(S ) , (S 1) |
|
( 1,2,3; |
s 1,2,3 ) в (8) удов- |
||||||||||||||||||
( ) |
0, |
|
( 1) |
0; |
|
( ) |
2 |
( 1) |
0 . |
|
|
|||||||||||||
летворяют условиям: S |
|
S |
|
|
|
S |
|
|
|
|
S |
|
|
|
|
|||||||||
2. Решение задачи
Задача (6)-(8) может быть решена методом суммарной аппроксимации, методом малого параметра, методом итерации, а также другими методами численного анализа. Здесь предпочтение отдали методу итерации, обоснованному в работе [8], методу аппроксимации [9], методу разложения по собственным функциям.
Пользуясь выбранными методами, решение задачи (6)-(8), приведенное к простейшему случаю, можно представить:
|
|
|
|
|
|
|
|
|
|
|
|
|
2 j |
|
|
2 j |
|
|
|
|||
|
|
1i |
|
|
|
|
|
1i |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x1 |
B1i sin |
|
|
|
|
|
x2 B2 j sin |
|
|
x2 |
|
|||||||||
H(x1, x2 , x3 ,t) Dijk cos |
2 1 |
2 1 |
x1 |
cos |
2 2 |
|
2 |
|
|
|||||||||||||
i 1 j 1k 1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
2 |
ijk |
|
|
45 x3 |
|
|
C |
2 t |
|
|
|
|
|
|
|
|||
|
V |
|
|
|
|
e |
|
2 |
|
e |
|
vn |
ijk |
. |
|
|
(13) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
ij |
45 |
|
K03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Здесь V ij (x3 ) – функция из комбинации функции Бесселя первого и второго
рода индекса ij ; |
ijk – |
положительные корни уравнения, |
|
составленного из |
||||||||||||||||||
комбинации этих функций, удовлетворяющим условиям (8); 1i |
и 2 j – поло- |
|||||||||||||||||||||
жительные корни уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
(1) |
(3) 12 |
|
(2) (4) |
|
|
(1) (3) |
|
22 |
|
|
(2) (4) |
|
|
|||||||
|
1 |
1 |
4l 2 |
|
|
1 |
1 |
|
2 |
2 |
|
4l 2 |
|
|
2 |
2 |
|
|
||||
ctg 1 |
|
|
1 |
|
|
|
|
|
, ctg 2 |
|
|
|
2 |
|
|
|
|
|
|
; |
||
(1) (4) |
(2) |
(3) |
|
1 |
(1) |
(4) |
|
(2) (3) |
|
2 |
|
|||||||||||
|
|
1 |
|
|
|
|
|
|||||||||||||||
|
1 |
1 |
|
1 |
|
4l1 |
|
2 |
2 |
|
|
2 |
2 |
|
4l2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Dijk – известные коэффициенты, определяемые из начально-краевых условий.
3. Определение осадок и результаты предварительных расчетов
Осадка соленого грунтового основания, вызванная нагрузкой q, согласно методу, предложенному в работе [5], и полученных решений (12), (13), определена формулой:
|
|
n |
0 |
( |
4 |
|
5 |
) |
|
h |
|
|
x |
|
|
|
|
|
|
|
|
|
S (t) |
|
|
|
|
|
|
0 |
e |
|
44 3 |
D1ij ch |
|
x |
|
F sh |
|
x |
|
|
|||
(1 |
0 )(1 (n 1) 2 ) |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
i 1 j 1 |
3ij |
|
3 |
ij |
3ij |
|
3 |
|
|||||||||
388

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов
|
|
|
|
2 ijk |
|
|
|
|
45 x |
|
|
|
|
2 |
|
|
|
|
|||||||||
|
Dijk V |
|
|
|
|
|
|
|
3 |
e |
Cvn |
|
ijkt |
|
|
||||||||||||
|
|
|
|
|
|
|
|
e |
|
2 |
|
|
|
|
dx3 . |
(14) |
|||||||||||
|
|
|
|
K |
|
|
|
|
|
|
|
|
|||||||||||||||
|
i 1 j 1 k 1 |
ij |
45 |
03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Предварительные расчеты по формуле (14) показали: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
осадок слоя соленых грунтов в |
|
0 |
10 20 |
30 40 50 60 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
t, сутки |
||||||||||||||||||||||
зависимости от растворимостей солей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
существенно (не существенно) отли- |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
чаются от осадки несоленых грунтов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|||
(рис. 2); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при |
незначительном |
модуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
мгновенной |
деформации вертикаль- |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ное перемещение верхней поверхно- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
сти уплотняемого массива не зависит |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
от времени; |
|
|
|
st, (см) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
учет неоднородности соленых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
грунтов, неоднородность |
которых |
|
|
|
|
I – при 5 = 0,05; II – при 5 = 0,9 |
|
||||||||||||||||||||
обусловлена переменностью возраста |
|
|
|
|
|
|
|
|
|
|
– для соленых грунтов; |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
– для несоленых грунтов. |
|
||||||||||||||||
их скелета в зависимости от про- |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Рис. 2 – Изменение осадка st по 1 от рав- |
||||||||||||||||||||||||||
странственных координат, достаточно |
|
|
|
номерно распределенной нагрузки |
|
||||||||||||||||||||||
заметно влияет на характер осадки |
|
|
|
|
|
|
|
|
|
|
|
|
q = 2кг/см2. |
|
|
|
|
||||||||||
грунтовых оснований во времени. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 . |
|
|
|
|
||||||
Это влияние может быть незначительным только при 39 |
|
|
|
|
|||||||||||||||||||||||
Литература
1.Алтынбеков Ш. Нелинейное определяющее уравнение состояния грунта и методика определения его параметров /Ш. Алтынбеков //PROCEEDINGS The international scientific-technical conference dedicated to the 20-th anniversary of National Engineering Academy of Republic of Kazakhstan. Part I.-Aktobe, 2010.-C.24-29.
2.Алтынбеков Ш. О некоторых современных вопросах фильтрационной теории консолидации неоднородных грунтов /Ш. Алтынбеков //Механика и моделирование процессов технологии.- Тараз: Изд. ТарГУ, 2006, №2.- С.328-329.
3.Цытович И.А. Прогноз скорости осадок оснований сооружений / И.А.Цытович, Ю.К. Зарецкий, М.В.Малышев, М.Ю.Абелеев, З.Г.Тер-Мартиросян – М.: Стройиздат, 1967.- 238 с.
4.Терцаги К. Механика грунтов в инженерной практике /К.Терцаги, Р.Пак.-М.: Гос. изд-во лит. по строительству, архитектуре и строительным материалам, 1958.- 607 с.
5.Флорин В.А. Основы механики грунтов /В.А.Флорин.- М.: Стройиздат, 1961.-
Т.2.- 543 с.
6.Алтынбеков Ш. Основное уравнение теории фильтрации соленых грунтов / Ш. Алтынбеков// Геотехника: теория и практика: Международный тематический сборник трудов.- Санкт-Петербург, 2013.- С.191-200.
7.Алтынбеков Ш. Коэффициенттері өзгеруші В.А.Флорин теңдеуі үшін бастапқы-шеттік жəне түйіндес есептер /Ш.Алтынбеков.- Шымкент: Нұрлы бейне, 2007.- 127 бет.
389

Современные геотехнологии в строительстве и их научно-техническое сопровождение
8.Алтынбеков Ш. Об одном методе аппроксимации /Ш.Алтынбеков// Узб. журнал «Проблемы механики», 1995.- №3-4.- С.5-7.
9.Алтынбеков Ш., Ширинкулов Т.Ш. Об одном итерационном методе нелинейнных краевых задач консолидации грунтов //ДАН РУз. Математика. Технические науки.
Естествознание. 1996, №1-2. С.25-27.
УДК 624.131.436
А.А. Коршунов, А.Л. Невзоров (САФУ, г. Архангельск)
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ПРОМЕРЗАНИЯ ДИСПЕРСНЫХ ГРУНТОВ В АВТОМАТИЗИРОВАННОЙ ЛАБОРАТОРНОЙ УСТАНОВКЕ
Морозное пучение грунтов является сложным процессом, который существенным образом зависит от двух составляющих: скорости миграции влаги к фронту промерзания и перемещения фронта промерзания. Первая из них определяется главным образом свойствами грунта (дисперсностью, влажностью, плотностью и др.), вторая – градиентом температуры. Чем медленнее промерзает слой грунта, тем больший объем влаги мигрирует к фронту промерзания, вызывая большее пучение [3, 4, 10, 11]. Существенное влияние скорости перемещения фронта промерзания на деформации пучения экспериментально подтверждено опытами Л.Б. Ганелеса, Ю.Р. Оржеховского, М.М. Юрганова, Л.В. Шевченко, В.Я. Лапшина и др. [2, 7, 8].
Скорость промерзания грунтов может быть определена по результатам лабораторных экспериментов или численного моделирования. При этом для получения достоверных результатов в ходе численного эксперимента необходимо определить поведение численной модели грунта, основываясь на данных экспериментальных исследований. Это может быть достигнуто путем сравнения результатов лабораторных и численных экспериментов и калибровки численной модели грунта.
Значительное отклонение скорости промерзания грунта в лаборатории от скорости промерзания в основании реального сооружения может привести к неправильной классификации грунта [5]. Для повышения достоверности и надежности определения степени пучинистости грунтов в лабораторных условиях в 2012 году разработана новая автоматизированная установка, позволяющая проводить испытания при заданных значениях скорости перемещения фронта промерзания [6].
АВТОМАТИЗИРОВАННАЯ УСТАНОВКА
Автоматизированная установка (рис. 1, 2) включает в себя ячейку с образцом грунта, выполненную из разрезных колец, нагрузочную раму, холодильную и морозильную камеры с возможностью контроля за температурой при помощи датчиков температуры, систему получения, обработки и передачи результатов измерений.
390
